ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
D. N. Dewangan1, Manoj Kumar Jha2, Y. P. Banjare3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The fault mode of steam-induced vibration, unbalance of rotating elements, misalignment of turbine shaft, rotor malfunction, oil film instability of bearing etc. are accountable for unreliable and uncertain failure of power plant. Experience of operators, maintenance policy execution of maintenance team and using standards codes of good practices by designers and manufacturers are reducing the potential failure modes of the system. The work investigate the reliability of steam turbines installed in a thermal power plant. Reliability estimation is based on a last five year historical failure database of two turbines of 500 MW, both are installed and commissioned at the same time. The method of reliability evaluation is based on concepts of system reliability, such as functional tree development, application of failure mode and effects analysis (FMEA) to categorize critical components based on a historical failure database to improve the system reliability. It is necessary to improve the reliability indices of the power plane by taking some measures such as well planned and routine maintenance of equipments as well as training and retraining of technical human resources of the major equipment.
Keywords |
| Reliability, Availability MTBF, MTTF, RCM, FMEA. |
I. INTRODUCTION |
| Steam turbine generator set is a key device of the power plant. For competent power plant, cost-effective production and long run performance, it is essential to maintain the power plant should run failure free. Reliability analysis have gradually recognized as standard tools for the designing, scheduling of operation and maintenance of any system. The reliability of power plant is related to the possibility of giving electricity efficiently and more economical with a reasonable quality assurance of continuity [Wang et al., 2002]. A modern power plant system can be divided into generation, transmission and distribution functional area. The system can be considered independently or in combinations of all three functional areas. This work is limited to the evaluation of the generation reliability. The main aim is to development a method to improve the reliability of the steam turbine power plant. In this respect, Reliability centered maintenance concepts are utilized as a guideline for ranking the maintenance policy priorities of the critical components of steam turbine. |
| The reliability of the system can be designated through the deterministically approach and/or probabilistic approach. Souza et al. (2012) deal with the probabilistic aspect of operational performance of power plant. In the work, deterministic approach of reliability analysis of the system is used to deals with understanding how and why a system is unsuccessful, and how it can be planned to avoid such failure from happening or re-happening. This includes analysis such as review of historical field failure reports, understanding scientific theory behind the failure, the role and degree of maintenance policies. Wang and Billinton (2003) reported that the role of a power plant is to provide electricity, resourcefully and with a reasonable guarantee of continuity and quality to its consumers. A modern power plant is very huge, multifaceted and highly integrated. Gupta and Tewari (2009a, and 2009b), Lakhoua, (2009) suggested that electric power plant can be divided into suitably subsystems or functional areas such as generation, transmission and distribution. Reliability studies may be carried out separately or in combinations of all three functional areas. This work is limited to the estimation of the generation reliability. |
II. RELIABILITY ESTIMATION OF STEAM TURBINE |
| The most acknowledged definition of reliability is the capability of an item, product, system, etc., to function under selected operating conditions for a specific period or number of cycles. Thus, the reliability is the possibility of a system to implement required task for a given period of time without any failure under specified conditions for which it is anticipated. The measure for reliability estimation of non-repairable systems is Mean Time to Failure (MTTF) and for repairable system is Mean Time between Failure (MTBF). Mathematically, reliability of a component for given period t can be represented as: |
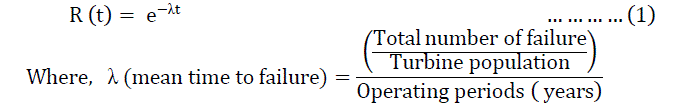 |
| The reliability of steam turbine has calculated based last five years historical failure database of two turbines of 500 MW, both are installed and commissioned at the same time. The reliability calculation is shown in Table 1. Mean time between failures (m), mean time to repair (ζ) and reliability is estimated by processing the historical fault data available. |
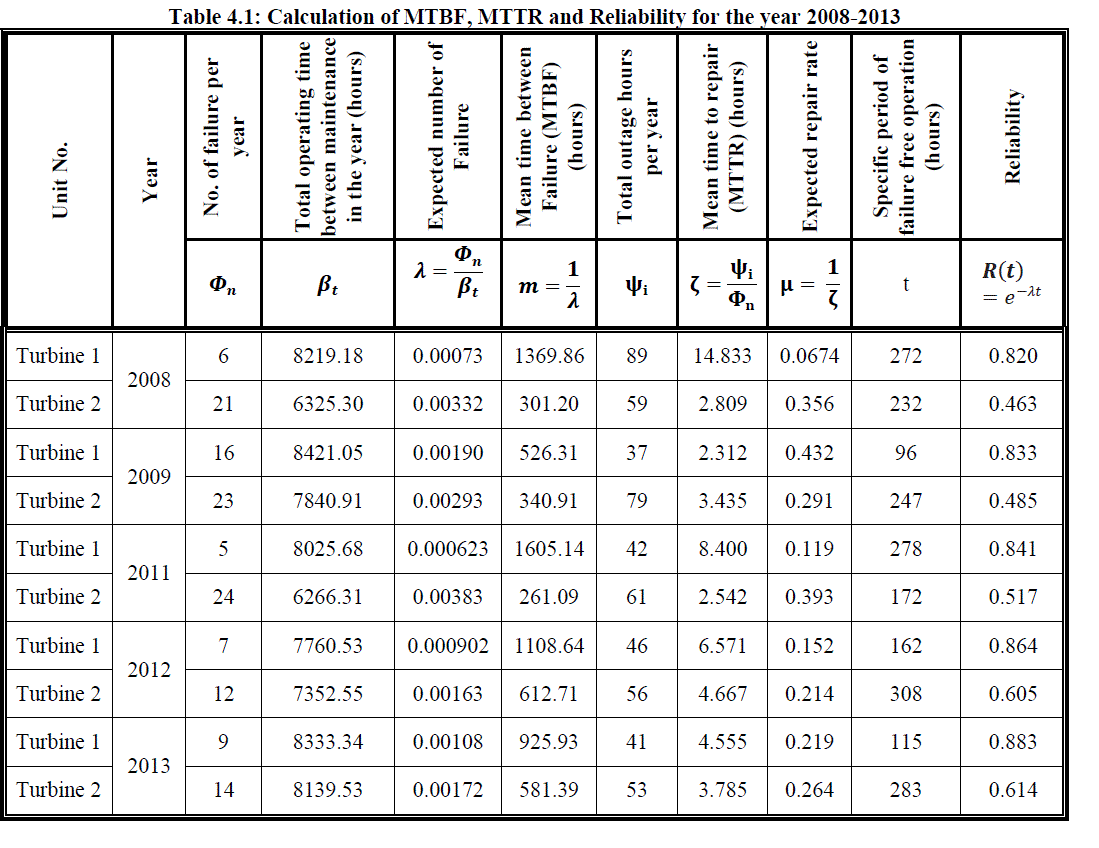 |
| Mean time between failures (m) is a ratio of total operating time between maintenance per year to the number of failure per year. It is the measure of arithmetic mean (average) time, in which period the equipment will execute a specified task before an unplanned failure will take place. Thus it is the reciprocal of the failure rate |
 |
| Where, λ = Expected no of failure, Φn = no of failures per year, βt = total operating time between maintenance in the year |
| Mean time to repair (ζ) is a ratio of total outage hours per year to number of failures per year. It is an inverse of expected repair rate. Hence, mean time to repair is quantified the average outage hours; the equipment can bring back to normal operating condition when it does fail. |
 |
| Where, ψi = total outage hours per year, Φn= number of failures per year and μ = expected repair rate. |
| It is assumed that failed system is immediately repaired, when we calculate the mean time between failures (MTBF). As a result, mean time to repair (MTTR) or repair rate is zero, in actual system this is impossible; thus, MTBF is considered as the sum of the MTTF and MTTR. In compare to MTBF, mean time to failure (MTTF) is a measure of average time to failures with the modeling hypothesis that the failed system cannot be repaired. The MTTF is basically the reciprocal of the failure rate. |
| Reliability R(t) is regarded as the capability of an equipment to execute its required function reasonably under given conditions during a stated period of time [Ireson et al. (1996), and Smith and Hinchcliffe (2004)]. Thus, reliability is a probability that the equipment is operating without failure in the specific time t. |
 |
| The investigation shows that steam turbine-2 has maximum failure rate and minimum reliability in comparison to turbine-1. Reliability of the steam turbine can be enhanced considerably by reviewing maintenance practices. Routine preventive maintenance should be given additional attention to improve the performance of power plant. |
III. RELIABILITY ANALYSIS OF STEAM TURBINE |
| The failure criterion of any component of steam turbine is incapability of generating the nominal power output. The reliability analysis is executed for two steam turbines installed in the power plant, submitted to same commissioning process and starting to function at the same time. Time to failure data has used for reliability analysis of a system. Mean time to failure (MTTF) is mostly used parameter to characterize reliability of a system. The mean time to failure is given by: |
 |
| Where, R (t) = reliability at time t, and t = time period (hours) |
| In the reliability analysis the Bath-Tub Curve (Figure 1) is broadly used for time dependent failure rate of components. Bath-Tub curve has three distinct regions: early life period, useful life period, and wear out period. A decreasing curve between time period t0 to t1 of the bath-tub curve represents the early life period (also known as infant mortality period) of the system. |
| Random failures are represented by the exponential probability function for expressing reliability phenomena. The failure modes in the starting of the operational life of steam turbine are not generally random therefore it cannot be represented by an exponential reliability distribution. The early failure mode of the steam turbine depends upon designing, manufacturing, commissioning, operational method, misalignment between cylinder and rotor, uneven radial clearance caused by improper installation and maintenance and even on environmental conditions. |
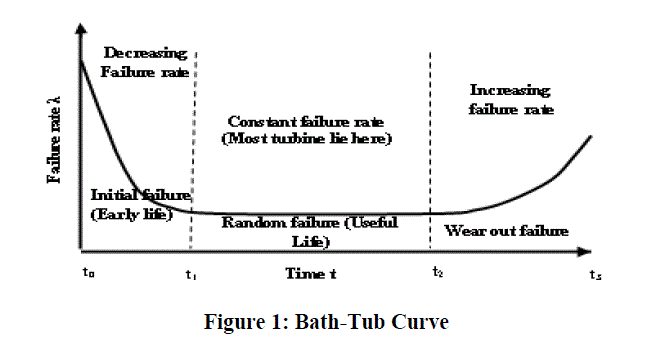 |
| The failure rate remains constant will remain constant during the useful life period of any system but failures will take place randomly. This is shown on the graph for time period t1 to t2. Erroneous utilization, human errors, and unsatisfactory design margins may be some of the source for failure in this period of life. These failures can be abridged by incorporating redundancy in the system. During wear out period (between t2 to t3) the possibility of failure rate has increases. In this period the failures takes place due to aging, misalignment, creep, friction, finite life of components and fewer preventive maintenance. These failures can be decreased by implementation of successful preventive maintenance policies and replacement of damaged components. When the aging effect (time related failures) and early failure are presented then the reliability of steam turbine is commonly estimated by Weibull probability distribution. |
| The reliability distributions are evaluated based on failure database. In case of wear-out or fatigue failures of the system, the Weibull distribution parameters (Weibull distribution shape parameter and Weibull distribution characteristic life) are characterized as follows: |
| Where, R(t)= reliability at time t, t = time period (hours), β = Weibull distribution shape parameter, η = Weibull distribution characteristic life (hours) |
| From time to failure data, The Weibull++ [Reliasoft, 2003] software has used for parametric assessment of steam turbine reliability analysis. Turbine 1 presented 43 failures that caused equipment unavailability in the analysis period. Most of them were related excessive vibration on the bearings, sensor calibration problems, control room problem, misalignment, uneven radial clearance caused by improper installation and maintenance etc. Turbine 2 presented 94 failures in last five operational years. These failures are related to poor stability of high-pressure cylinder bearing, operating parameters changed, calibration problems of pressure gauges, steam distribution mechanism, uneven radial clearance, , sealing system problem, piping system, speed and eccentricity sensor calibration problem. Steam flow control system problem etc. |
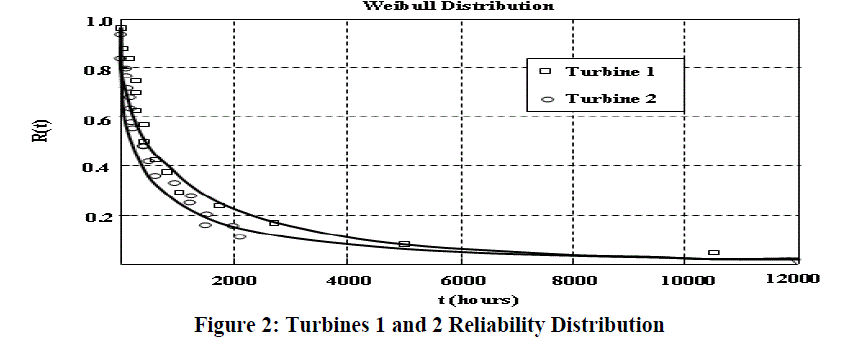 |
| The reliability distribution curve for turbine 1 and 2 are presented in Figure 2. The reliability distribution curves provide evidence of adherence of the reliability distribution to the historical failure data. The Weibull distribution parameters are given in Table 2. The Weibull shape parameter (β) of the steam turbine 2 is smaller than the steam turbine 1. The reliability distributions with shape parameters of both turbines are less than one. Whenever, shape parameter (β) value lies between 0 and 1, the reliability distribution has a declining failure rate. This indicates that the turbine 1 is closer to the period of random failures. Some minor differences in the assembly and set up processes cause a huge number of failures in the last five years of operation of turbine 2. Once the turbine has failed, a remedial maintenance procedure is executed to bring back the equipment to normal operating condition |
 |
| The repair rate is also a random variable since it is dependent on the nature of failure, ability to analyze the root cause of failure and expert human resources to carry out the repair procedure. The possibility that equipment will be repaired in a specified period of time is characterized by maintainability and represented by a lognormal distribution. The maintainability of a system can be given as follows: |
 |
| Where: M (t) = maintainability at time t, μ = lognormal distribution mean value, σ = lognormal distribution standard deviation, Φ = standard normal distribution cumulative function |
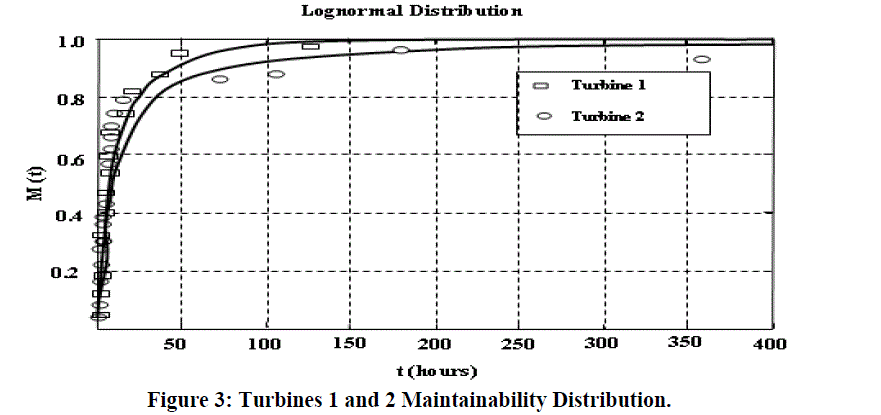
| The maintainability probability distribution curve for steam turbines 1 and 2 are presented in Figure 3. The analysis of the failure database shows that turbine 2 has a mean time to repair greater than turbine 1. The steam turbine availability can be estimated after the reliability and maintainability parameters calculation. In the case of a steam turbine in a power plant, availability is assessed the time period; a system can generate the nominal power output. Mean time to failure and mean time to repair are two parameters which controlled the availability of steam turbine. |
 |
IV. METHOD DEVELOPMENT FOR RELIABILITY IMPROVEMENT OF STEAM TURBINE |
| The reliability of the steam turbine can improve by using the RCM concepts. Reliability Centered maintenance concepts are used as a guideline for ranking the maintenance policy priorities for the critical components. It has considered the new maintenance methods, which reduced the corrective maintenance and repair time [Souza et al. (2009)]. The reliability estimation of steam turbines are based on RCM based system reliability concepts. This method is applied to investigate of two similar heavy-duty steam turbine of 500 MW each. |
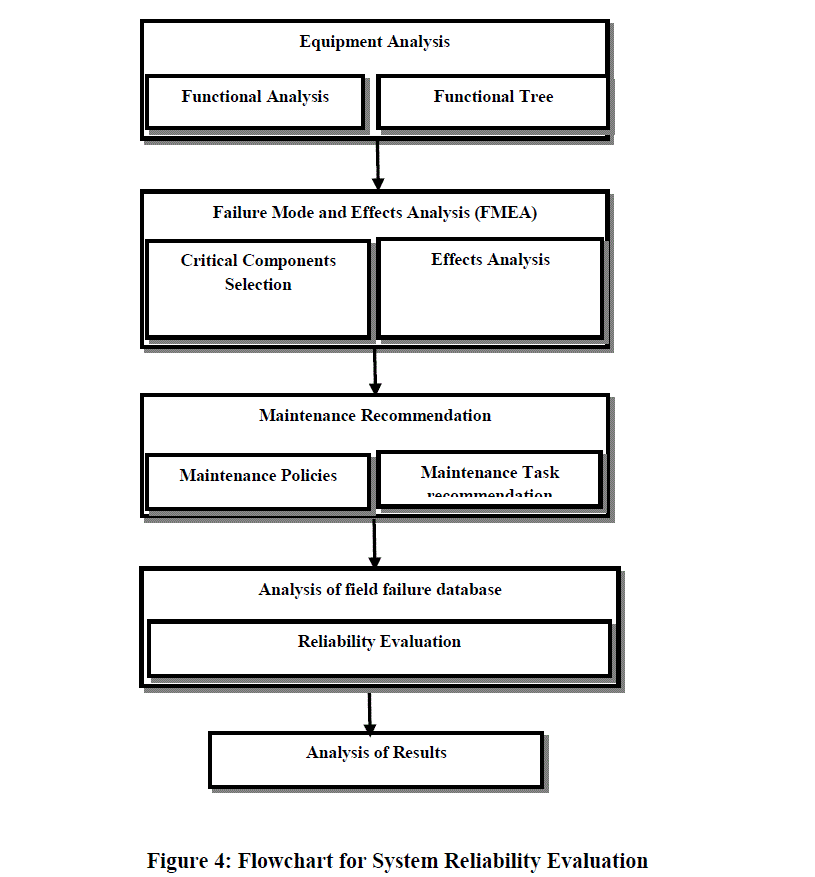 |
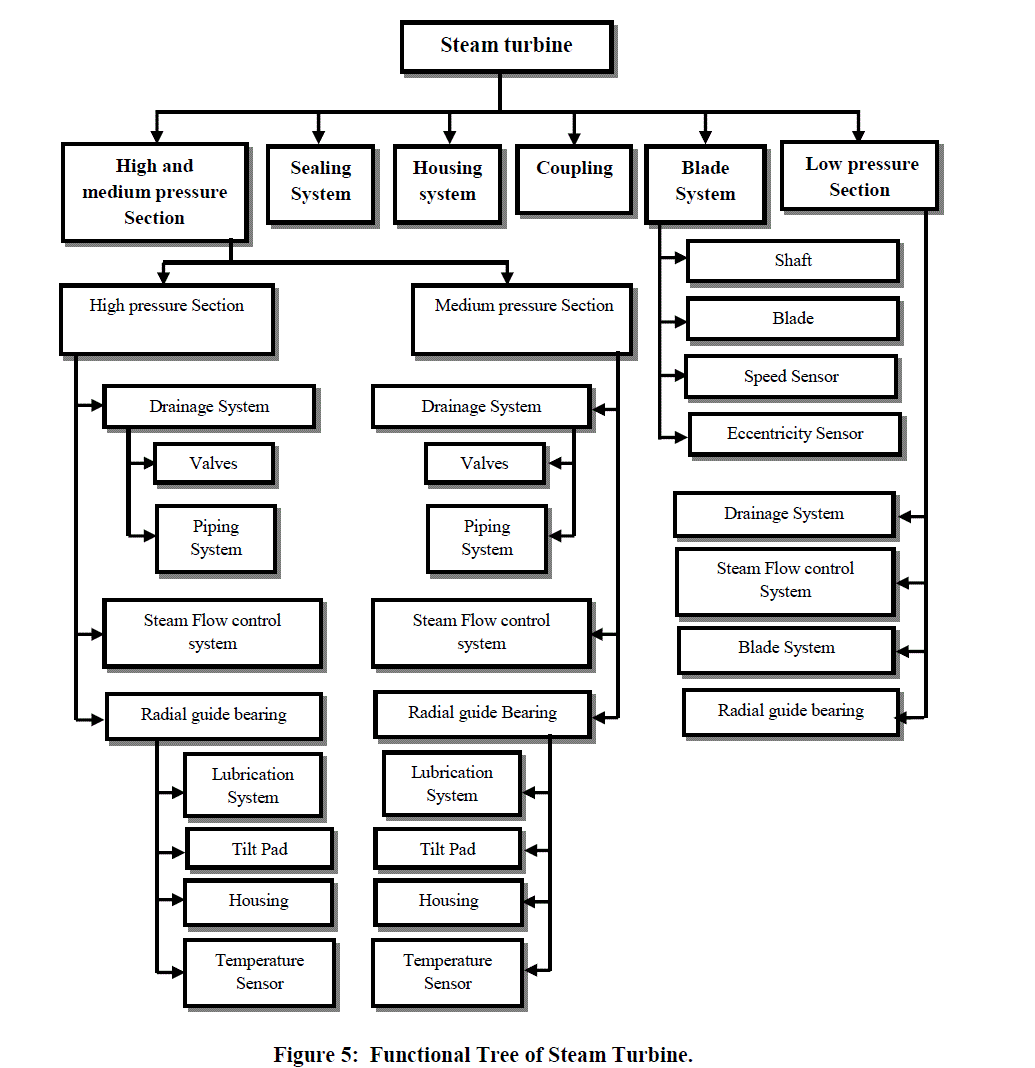
| The system reliability concept comprises development of functional tree, use of failure mode and effects analysis (FMEA) and maintenance recommendations. A flowchart (Figure 4) is used to illustrate the most important steps of system reliability analysis method. The first step of method is preparation of steam turbine functional tree that allows the organization of the functional links between the equipment subsystems. The functional tree for the steam turbine is divided into six main systems: high and medium pressure section, low pressure section, housing system, sealing section, coupling, blade system. Each main system further divided into subsection as shown in Figure 5. |
 |
| The identification of the most critical components of steam turbine during operation is taking into consideration in the second step. The failure mode and effect analysis (FMEA) is always based on a table which contains mainly four columns. In the first column the component under study is listed and in second column the physical modes of failure are given. The potential causes of failure modes of each components of the functional tree are describe in third column. Finally, the last column lists the effects of each failure mode are categorized according to the criticality scale, which states the degradation degree in the turbine operation. Lewis (1987) has proposed FMECA (Failure Mode and Effective criticality Analysis) approach to evaluate the component failure effect on the turbine operation The FMECA analysis was performed for each component listed in the end of a given branch of the functional tree. For present analysis criticality index is classified into three main severity levels: marginal, critical and catastrophic For the definition of the system degradation, the FMECA analysis uses a numerical code, usually ranking from 1 to 10. Higher the number, criticality of the component is higher |
| In third step, based on the results of the FMEA analysis, the RCM concepts can be used to recommend maintenance tasks to those components that have a criticality index greater than 6. The failure of those components can cause severe degradation in the steam turbine performance. This maintenance policy is emphasized on the use of predictive or preventive maintenance, inspection and overhaul maintenance tasks. The main aim of this maintenance policy is the decrease of unpredicted failures during normal operation of the component [Smith and Hinchcliffe, 2004]. The RCM methodology is explained by conserve the operating functions; categorize failure modes that can defeat the functions and selection of main monitoring systems which assess the critical component degradation which permit the maintenance actions prior to the incident of functional failure. The equipment availability can be improved by condition-based maintenance policy. |
 |
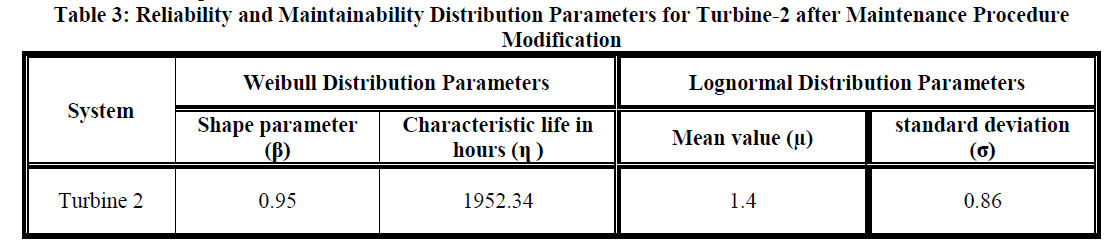
| The next step involves a reliability analysis based on the time to failure data recorded during the steam turbine operation. The reliability of the steam turbine is estimated based on the failure data. The steam turbine availability is evaluated with considering the time to repair data and the preventive maintenance tasks related with the system. As Table-3 represents that the reliability parameters and maintainability probability distributions parameters of steam turbine are improved using the RCM concepts of maintenance. |
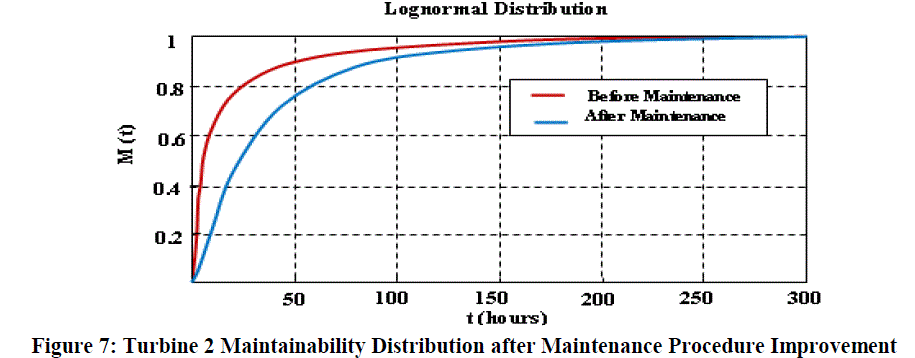 |
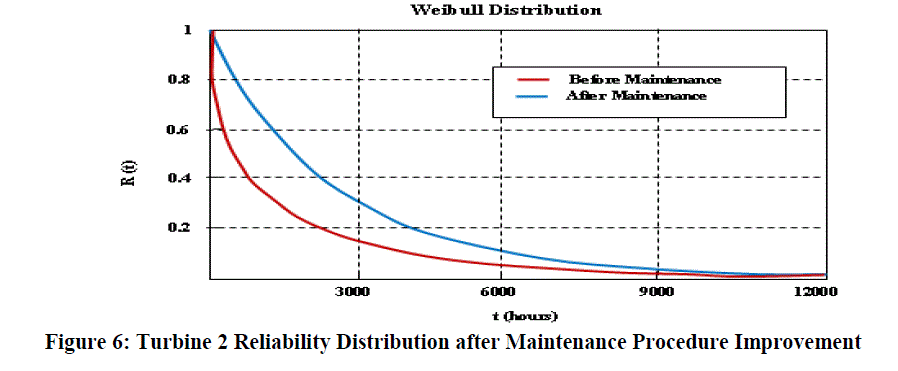
| Figure 6 presents the reliability distribution before and after maintenance procedure. The estimated mean time to failure of turbine 2 improved to 1952.34 hours. After the use of a condition based maintenance policy for critical steam turbine components, the shape parameter (β) of the Weibull distribution for turbine 2 is improve to very close to one, which indicates that the equipment is now presenting random failure. |
| As well as the lognormal distribution of maintainability shows that there is reduction of lognormal distribution parameters, which indicate that the failure of the steam turbine 2 is reduced. The planned maintenance tasks will reduce the number of unplanned or emergency trips of the steam turbine. The availability of steam turbine 2 has increased in one operational year which is very close to the turbine 1. Figure 7 represents the maintainability distribution before and after maintenance procedure. |
 |
V. CONCLUSION |
| The reliability characteristics of any heavy duty steam turbine depends upon the various factor such as on-site installation process, skill of operators, training of maintenance team, environmental variables and steam quality. The proposed method can defines quantitatively the system reliability and availability. The system reliability can be examined through using of time to failure and time to repair database. The investigation is based on the last five year operational database. The enrichment of historical database with additional failure and repair data during future operational years will permit more reliable estimation of the turbines reliability. Training and retraining of technical human resources on the major equipment, well planning and more regular scheduled maintenance can improve the reliability indices of the plant. |
References |
|