ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Vasanthi J1, Ranjith Balakrishnan*2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
An enhancement of data protection system for secret communication using reserve room in encrypted images based on texture analysis with lifting wavelet is proposed here. The reserving space to conceal text messages was the reserve space. RSA asymmetric key encryption is used here to encrypt secret text before hiding for increasing the security. Adaptive least significant bit algorithm utilized for concealing the encrypted text into the effectively done in an image spectral domain and chaos crypto system used to encrypt the image frequency components except reserved space. An experimental result shows that used methodologies generated minimal error with high PSNR rate at various data hiding capacity.
INDEX TERMS |
| Reversible data hiding, chaos encryption, LSB replacement, RSA key encryption |
INTRODUCTION |
| Steganography is widely used in medical and military imagery for secret data communication. The proposed system uses reserve room before encryption approach to overcome the problem of prior methods such as vacating room after encryption and pixel difference expansion. In existing practice, pixel difference expansion based RDH is the spatial domain process to conceal secret text messages within a cover image. The data hiding involves histogram adjustment to reduce overflow and underflow errors and adjacent pixels are subtracted to determine the differences values. Then difference will be either incremented or decremented based on message bits. This technique produces the spatial distortion leads to degrade an image quality and it is less compatible and complex one. This will be overcome by the method of least significant bit replacement algorithm. In Vacating room after encryption, the secret messages are concealed into encrypted domain by replacement of some pixel intensities. This spatial domain technique distorts an image quality wherever the secret message bits were hidden. With the consideration of these problems, the system proposes the reserve room approach with lifting wavelet transformation for preserving an image quality and improve the security of transmission. The technique lifting wavelet decomposes an image into frequency sub bands which contains approximation and detailed coefficients. The system will reserve the coefficients from detailed components which have texture, edges and region boundary. It is insensible region for human visual system. In addition with this approach, chaos crypto system, adaptive least significant bit replacement will be used for image encryption and message embedding. Data recovery is the reverse process of the encryption and embedding to get lossless extracted image and messages. The simulated result shows performance of the used methodologies in terms of metrics evaluation such as mean square error, peak signal to noise ratio and correlation coefficients. |
II. RELATED WORKS |
| This paper [1] suggested by Hemalatha et al provides a novel image steganography technique to hide both image and key in color cover image using Discrete Wavelet Transform (DWT) and Integer Wavelet Transform (IWT). This paper has no visual difference between the stego image and the cover image. The extracted image is also similar to the secret image. This is proved by the high PSNR (Peak Signal to Noise Ratio), value for both stego and extracted secret image.The results are compared with the results of similar techniques and it is found that the proposed technique is simple and gives better PSNR values than other. The major objective of steganography is to prevent some unintended observer from stealing or destroying the confidential information. IWT is a more efficient approach to lossless compression. The coefficients in this transform are represented by finite precision numbers which allows for lossless encoding. This wavelet transform maps integers to integers. In case of DWT, if the input consists of integers (as in the case of images), the resulting output no longer consists of integers. Thus the perfect reconstruction of the original image becomes difficult. However, with the introduction of Wavelet transforms that map integers to integers the output can be completely characterized with integers. |
| A.Key Embedding |
| The key obtained in the previous subsection is hidden in the cover image using IWT. The steps are as follows: Find the integer wavelet transform of Cr component of the cover image. Replace the least significant bit planes of the higher frequency components of the transformed image by the bits of the key. Obtain the inverse IWT of the resulting image to get the stego Cr component. Represent the resultant image in RGB color space to obtain stego image G. |
| B.Key Extraction |
| The secret image can now be extracted from this image using the following steps: Represent the stego image G in YCbCr color space.Find the integer wavelet transform of Cr component of the stego image G. Obtain the key from the least significant bit planes of the higher frequency components of the transformed image. Convert back to RGB representation. Decompress the key and then decrypt it to get original key. This paper [2] suggested by Weiming Zhang et al explains that the Reversible data hiding (RDH) has the Capability to erase the distortion introduced by embedding step after cover restoration. It is an important property that can be applied to many scenarios, such as medical imagery, military imagery and law forensics. Many RDH techniques have been proposed based on three fundamental strategies: lossless compressionappending scheme, difference expansion (DE) and histogram shift (HS).In order to extract data, the two methods rely on decrypted images which may be unknown for some cases. Aiming for separating data extraction from image decryption, Zhang found the syndromes of a low-density parity check matrix to compress the LSB’s of the encrypted image. By doing so, an extra space is created to append additional data. These techniques can only achieve low embedding capacity (achievable largest embedding rate) or generate marked image with poor quality for high embedding capacity and subject to some errors on data extraction and/or image restoration. By modifying the estimating errors. In general, the excellent performance can be achieved in three different prospects: The proposed method is completely reversible. That is, no error happens in data extraction and image recovery steps. The PSNR values of marked decrypted image are much higher than those methods can achieve under given embedding rates. The extraction and decryption steps are independent, which are more natural and applicable. |
| The proposed method is composed off our primary steps: vacating room and encrypting image, data hiding in the encrypted image, data extraction and image recovery. Two different schemes, extraction before encryption and Decryption before extraction, are raised to cope with different applications. To improve the performance by reversing the order of encryption and vacating room and achieves excellent performance in three aspects: complete reversibility, higher PSNR under given embedding rate, separability between data extraction and image decryption. This paper [3] proposed by Xinpeng Zhang, describes that a content owner encrypts the original uncompressed image using an encryption key. Then, a data-hider may compress the least significant bits of the encrypted image using a data-hiding key to create a sparse space to accommodate some additional data. With an encrypted image containing additional data, if a receiver has the data-hiding key, he can extract the additional data though he does not know the image content. If the receiver has the encryption key, he can decrypt the received data to obtain an image similar to the original one, but cannot extract the additional data. If the receiver has both the data-hiding key and the encryption key, he can extract the additional data and recover the original content without any error by exploiting the spatial correlation in natural image when the amount of additional data is not too large. In the data embedding phase, some parameters are embedded into a small number of encrypted pixels, and the LSB of the other encrypted pixels are compressed to create a space for accommodating the additional data and the original data at the positions occupied by the parameters. Data Extraction and Image Recovery. In this phase, we will consider the three cases that a receiver has only the data-hiding key, only the encryption key, and both the data-hiding and encryption keys, respectively. With an encrypted image containing embedded data, if the receiver has only the data-hiding key, he may first obtain the values of the parameters and from the LSB of the selected encrypted pixels. Then, the receiver permutes and divides the other pixels into groups and extracts the embedded bits from the LSB planes of each group. When having the total extracted bits, the receiver can divide them into original LSB of selected encrypted pixels and additional bits. Note that because of the pseudo-random pixel selection and permutation, any attacker without the data-hiding key cannot obtain the parameter values and the pixel-groups, therefore cannot extract the embedded data. Furthermore, although the receiver having the datahiding key can successfully extract the embedded data, he cannot get any information about the original image content. Consider the case that the receiver has the encryption key but does not know the data-hiding key. Clearly, he cannot obtain the values of parameters and cannot extract the embedded data. However, the original image content can be roughly recovered. Denoting the bits of pixels in the encrypted image containing embedded data then the receiver can decrypt the received data. |
III. PROPOSED SYSTEM |
| A.LIFTING WAVELET TRANSFORM |
| The wavelet transform has gained widespread acceptance in signal processing in general and in image compression research in particular. In applications such as still image compression, discrete wavelets transform (DWT) based schemes have outperformed other coding schemes like the ones based on DCT. Since there is no need to divide the input image into non-overlapping 2-D blocks and its basis functions have variable length, wavelet-coding schemes at higher compression ratios avoid blocking artifacts. Because of their inherent multi -resolution nature, wavelet-coding schemes are especially suitable for applications where scalability and tolerable degradation are important. Recently the JPEG committee has released its new image coding standard, JPEG-2000, which has been based upon DWT. |
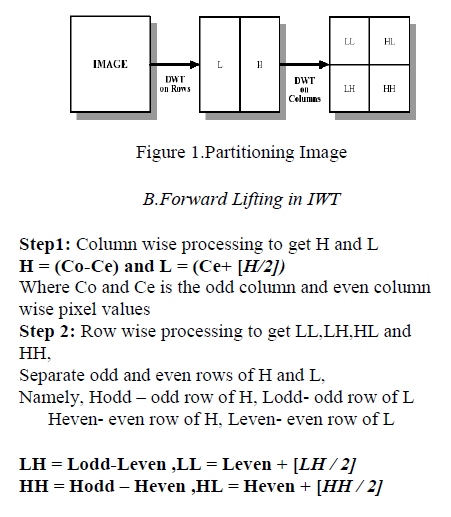 |
Reverse Lifting scheme |
| Inverse Integer wavelet transform is formed by Reverse lifting scheme. Procedure is similar to the forward lifting scheme. |
 |
| Here logistic map is used for generation of chaotic map sequence. It is very useful to transmit the secret image through unsecure channel securely which prevents data hacking. The chaotic systems are defined on a complex or real number space called as boundary continuous space. |
| The chaotic sequence will be defined by, Cn+1= U* Cn*(1-Cn) and encrypted pixel form defined by E = bitxor (P, Cn+1) |
| D.Asymmetric key Cryptography |
| Cryptography allows secure transmission of private information over insecure channels (for example packetswitched networks).Cryptography also allows secure storage of sensitive data on any computer. |
| E. RSA – Public Key Cryptography |
| Public key (E) and Modulus N are known to all users Private key (D) (secret key) Provides Authentication/Encryption Signing/Decryption operation Verifying/Encryption operation. Data encryption will be done by, |
| Cipher_text = C.^E mod N |
| Where, C – Each Character of Input text message |
| N = p * q; |
| N – modulus parameter, p & q – two largest prime number obtained from user given 8-bit key. Data decryption will be done by, |
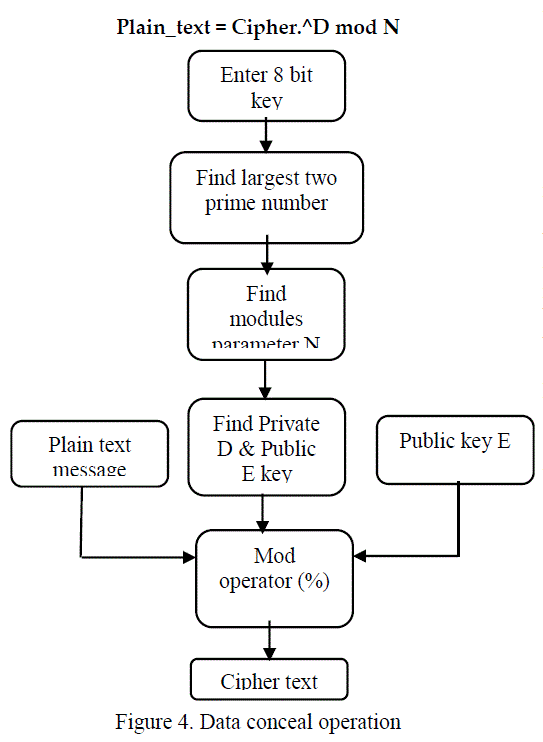 |
| F.DATA CONCEALMENT |
| The objective of steganography is a method of embedding additional information into the digital contents that is undetectable to listeners. We are investigating its embedding, detecting, and coding techniques. The idea behind the LSB algorithm is to insert the bits of the hidden message into the least significant bits of the pixels. As the application domain of embedding data in digital multimedia sources becomes broaden, several terms are used by various groups of researchers, including steganography, digital watermarking, and data hiding. The most frequently used steganography method is the technique of LSB substitution. In a gray-level image, every pixel consists of 8 bits. One pixel can hence display 28=256 variations. The weighting configuration of an 8- bit number is illustrated. The basic concept of LSB substitution is to embed the confidential data at the right most bits (bits with the smallest weighting) so that the embedding procedure does not affect the original pixel value greatly. The mathematical representation for LSB method is: x represents the i th pixel value of the stegoimage, ix represents that of the original cover-image, and im represents the decimal value of the i th block in confidential data. The number of LSBs to be substituted is denoted as k. The extraction process is to copy the krightmost bits directly. Mathematically the extracted message is represented as: Hence, a simple permutation of the extracted i m gives us the original confidential data. This method is easy and straightforward. However, when the capacity is greatly increased, the image quality decreases a lot and hence a suspected stego-image results. Furthermore, the confidential data might be easily stolen by simply extracting the k-rightmost bits directly.A 8-bit gray scale image matrix consisting m × n pixels and a secret message consisting of k bits. The first bit of message is embedded into the LSB of the first pixel and the second bit of message is embedded into the second pixel and so on. The resultant Stego-image which holds the secret message is also a 8-bit gray scale image and difference between the cover image and the Stego-image is not visually perceptible. The quality of the image, however degrades with the increase in number of LSBs. This hiding process will introduce the error between input and output image and it is determined by mean square error and Peak signal to noise ratio determines the image quality |
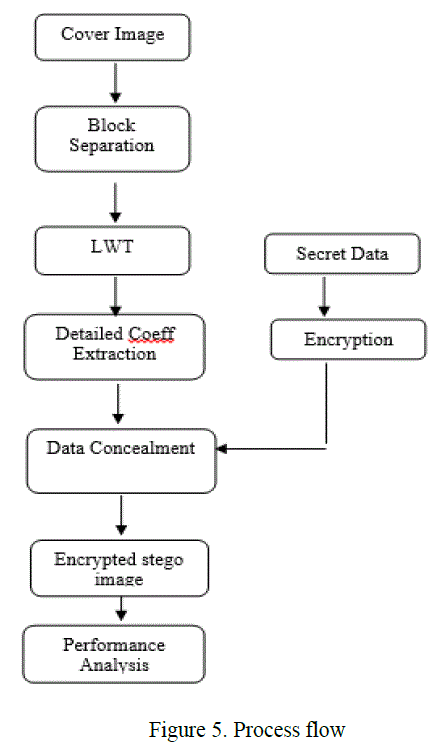 |
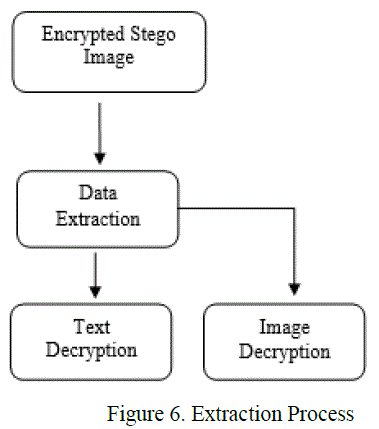 |
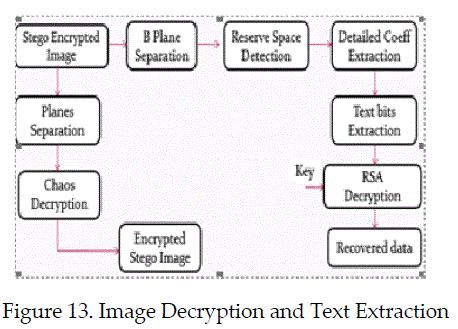
| In this process decryption of the data and the stego image should be done before the data can be extracted. |
 |
 |
| The main aim is that is to provide additional security by encrypting the data also, then the PSNR value is increased thus enhancing the quality of the image during the decryption process. |
 |
V. CONCLUSION |
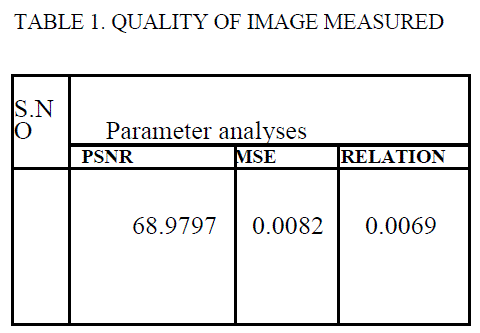
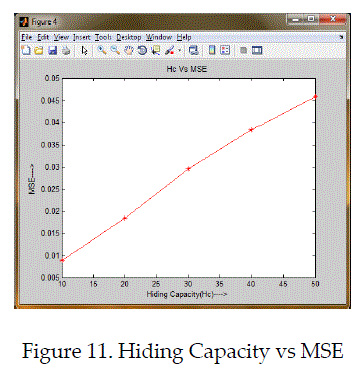
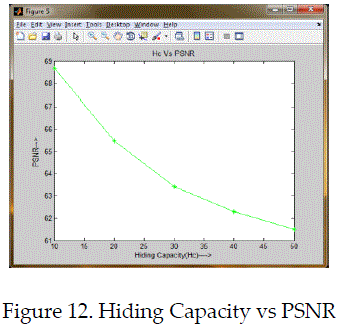
| This paper presented that protection of medical image quality and hidden the patients data during transmission based on approach of reserve room technique and chaotic crypto system with LSB based data concealment. Here, reserved space was done by lifting transform for concealing data effectively and chaos encryption was used as to protect image contents. This system was generated the stego image with less error under maximum data hiding capacity. Finally, the performance of system was evaluated with quality metrics such as error and PSNR factor. It was better compatible approach and flexibility with better efficiency rather than prior methods. |
 |
 |
VI. ENHANCEMENT |
| Data Extraction and after the decryption process will be carried out based on, Chaos decryption and Adaptive LSB bits Extraction are utilized to recover the image and extract the text messages. By using Private key an extracted cipher text will be decrypted to recover the data. Finally, image and hidden text will be recovered without any loss. |
 |
References |
|