International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

SIDELOBE DEDUCTION BY PIECEWISE NON LINEAR FREQUENCY MODULATION WAVEFORM

DjoeIsac Thomas1, C. Kamalanathan2, Dr. S.Valarmathy3
 1PG Scholar, Dept. of ECE, Bannari Amman Institute of Technology, Sathyamangalam, TamilNadu, India
2Asst. Professor (Sr. Grade), Dept. of ECE, Bannari Amman Institute of Technology,Sathyamangalam, TamilNadu, India
3Prof. & HoD, Dept. of ECE, Bannari Amman Institute of Technology, Sathyamangalam, TamilNadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The Linear Frequency Modulation (LFM) waveform is the most commonly and extensively used signal in practical radar system. This paper introduces a new scheme of Piecewise Nonlinear Frequency Modulation (PNFM) for generating good code sets. Each code set has good autocorrelation with small peak sidelobes and cross-correlation. A weighting function is usually applied in order to reduce the sidelobes. In an effort to achieve low autocorrelation sidelobe level without applying weighting function, PNFM signal has been investigated. The new class codes is shown to have good ambiguity function with the ability to tolerate a realistic range of Doppler shift. At the receiver a matched filter is used which improvement in Doppler detection with good SNR

Keywords
Piecewise Nonlinear Frequency Modulation, LFM, Ambiguity function, Chirp code, Radar

INTRODUCTION
Chirp system are the only spread spectrum system that do not normally employ a code sequence to control their output signal spectra. Chirp signal is generated by sliding the carrier over a given range of frequency in a linear or some other known manner during a fixed pulse period as shown in figure 1. The chirp spread spectrum receiver can employ a matched filter [7] to reassemble the time-dispersed carrier power. Chirp signals are angle modulated sweeping signals. It can be linear, that is time-bandwidth is constant or non-linear way for the whole frequency bandwidth B (Hz) by a sinusoidal waveform of constant amplitude within a certain time (Ts). If the sequence of frequency is swept from the lowest to the highest frequency limit, we called it as up-chirp. In the opposite direction it is down-chirp. The bandwidth of signal inside the pulse are very high hence it is spread spectrum modulation technique and gets the advantage of spread spectrum. When passed through a matched filter, this technique gives implementation of pulse compression [17]. For a given range resolution, pulse compression results in increased sensitivity.Pulse compression techniques have recently become more attractive, because of lower average power, higher sensitivity and higher scanning speed with increasedresolution. Hence the chirp spread spectrum is more suitable for spread spectrum radar altimeter design.
The importance of chirp waveform in proposed scheme has following advantages. First the constant envelope of time domain waveform leads to a maximum efficiency of the transmitted module. Second, the chirp spectrum approaches a regular sinc shape as time-bandwidth product increases so that its spectral efficiency and signal-to-noise ratio can be maximized. Finally exploit the linear frequency-time characteristics of chirp in signal processing.
The recent chirp system discussion such as classic chirp, spread spectrum system uses Surface Acoustic Wave (SAW) devices for chirp spreading and dispreading via SAW filtering. Most of the mature solution reaches lower Ultra Wide Band (UWB) based on binary sequence spreading [7, 10]. On the other side, there is fast pace development of the lowcost and low-power CMOS RF technology on which the majority of low-power UWB solutions are based.
The radar receiver is mainly divided into front-end processing and back-end processing. The front-end processing consists of down converting the received RF signal. The components of front-end receiver are antenna, pre-filter, low noise amplifier (LNA), mixer for fixing of receiver signal with local oscillator or the transmitted signal. In this process of mixing the high frequency is down converted to lower frequency. It is further divided and mixed with quadrature mixing 90º shifted local oscillator. This signal is further amplified with LNA. The splitted intermediate frequency (IF) converted to digital by Analog to digital converter (ADC).The back-end processing starts from processing of signal for detection of range (distance) and velocity. The digital signal is processed by the DSP processor in digital domain or frequency domain. In back-end processing of the receiver, signal is compressed in frequency domain which can be regarded as dual to pulse compression reduces time-bandwidth (TB) product of the signal. Thus the number of samples needed to sample the compressed signal can be reduced.
The time side lobes suppression is realized thanks to weighting operation being a result of intended introduced mismatch to the filter. Unfortunately, such the operation causes moreover losses concerning the output signal that causes the radar range limitation among others. The nonlinear frequency modulation (NLFM) signal application is the other method for the time side lobe suppression. Such the method islossless but for the signal synthesis it needs complicated analytical tools. Moreover, the NLFM signal is more sensitive for the Doppler effect.
The purpose of this paper is to evaluate the Piecewise Linear Frequency Modulated Pulse Compression (PLFM) [1] and propose Piecewise Non Linear Frequency Modulation (PNFM). The ability of PNFM is increasing effective power and sensitivity, as well as producing good quality estimates of radar measurable. The objective of this paper is to use a good class of PNFM codes that form sets such that all codes in each set have superior autocorrelation and such that every pair in the set has miniature cross-correlation. This is in addition to preserving the Doppler Tolerance and Detection properties (improved further with the use of an extended matched filter), as in the Triangular FM [1]. These old codes set applied for, where time duration and frequency sweeps are fixed belonging to the set. The new class of good code sets is compared to related classes that could be formed by changing the chirp rate while keeping the time-bandwidth product constant.

II. GENERAL CONCEPTS
Pulse compression (PC) is of wide use in radar systems to increase return energy without an increase in power, via relatively long pulses of sufficient time-bandwidth, so that no degradation in range resolution occurs. Assuming an additive white noise environment and a stationary point scatter there is no better processor than the matched filter. Pulse compression obviates the tradeoff between radar probing distance (and the need for high energy) and range resolution (short pulses desired) by internal modulation of a long pulse, and has significantly contributed to the development of radar systems since the 1950s. Sidelobe deduction has good application in radar and radar related application. Radar systems detect both the range (distance) and the Doppler (speed) of a target, whether it is on the ground or in space. Chirp waveforms are utilized in radar systems in order to detect both range and speed, simultaneously [17]. A chirp waveform is essentially a sinusoid with a frequency that varies over time. For the purposes of this research project the time-domain chirp is defined as the following:
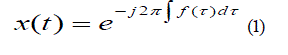image
where f ( ) is the linear chirp on a frequency vs. time plot.
Piecewise linear chirp is a new approach used to optimizing the radar chirp. The frequency vs. time characteristic of the chirp is required to be piecewise linear. Gradually changing the frequency of the chirp instead of instantaneously varying it could potentially yield more desirable spectral characteristics [2]. Two main goals exist for this chirp optimization: 1 the energy within the band of the chirp signal must be maximized, and 2 the in-band evenness should be as flat as possible while the spectrum is contained by a regulatory spectral mask.
Pulse compression radar is the practical implementation of a matched-filter system. The received echo is fed into a matched filter whose frequency response is the complex conjugate H*(ω) of the coding filter. The output of the matched filter, y(t) is the compressed pulse which is just the inverse Fourier transform of the product of the signal spectrum and the matched filter response.
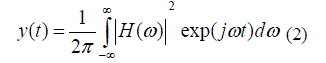image
A filter is also matched if the signal is the complex conjugate of the time inverse of the filter‟s impulse-response. This is often achieved by applying the time inverse of the received signal to the pulse-compression filter.
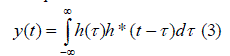image
In the chirp case this function is implemented by taking the product of the received signal with the transmitted signal and filtering to obtain a constant frequency beat. Spectrum is then determined using the Fourier transform or a similar spectral estimation process.
The ambiguity function [16] as shown in figure 4 is the time response of a filter matched to a given finite energy signal when the signal is received with a delay and a Doppler shift relative to the nominal values expected by the filter. No matter how we design our waveform, the volume of the ambiguity function remains constant.
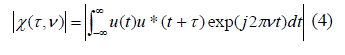image
LFM increases the bandwidth and subsequently improved the range resolution of the signal by a factor equal to the time bandwidth product. However, relatively high peak sidelobes remain in the autocorrelation function are unacceptable in some radar applications, where more than one target is present, giving rise to echo of different amplitudes. Three major techniques have been implemented to obtain lower sidelobes level, i.e., (1) weighting in time domain, (2) frequency domain weighting and (3) NLFM [2,5,6]. NLFM waveform is designed as matched filter response satisfies the sidelobe requirements. Since the receiver is matched with to the signal shape, no mismatch losses as in time domain weighting and frequency domain weighting. Several papers suggest that an issue for NLFM waveforms is their tolerance to Doppler shifts, i.e., maintaining their desirable sidelobe properties when Doppler shifted. However Johnson and Fairhead [22] state “the choice of window function [i.e. desired PSD taper for NLFM design] appears less important than previously supposed, although the truncated Gaussian window does give slightly better tolerance than the others to Doppler shift.” Morgan [23] proposes a hybrid approach to deal with this. It is easy to notice that the autocorrelation function side lobes level and their structure are much better in the case of the NLFM signal than in the case of LFM signal despite the mainlobe broadening. New proposed method called Piecewise Non- Linear FM (PNLFM) is similar to NLFM but has the advantage of time sidelobe reduction.

III. MATHEMATICAL MODELING AND PROCESSING
A. Ideal linear chirp pulse
Both the transmitter and receiver uses a linear chirp pulse generator. In the generator, ideally linear chirp pulse of central frequency f0, duration Tp and frequency sweep of f c is generated. Instantaneous chirp frequency can be expressed as
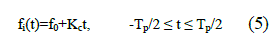image
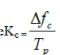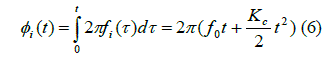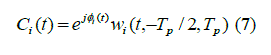where image is chirp phase of its instantaneous frequency
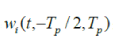image
image
where image is the rectangular window function with limit t1 and t2.
Time bandwidth product gives the number of independent complex samples needed to characterize the waveform
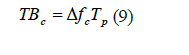image
B. Non-ideal linear chirp pulse
Linear VCO that would typically use linear chirp pulse never has an ideally linear turning curve
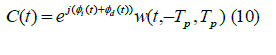image
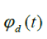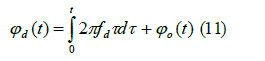here image is the chirp phase non-ideality function
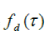image
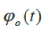where image is chirp frequency error image is phase modulation by the system component.
C. Practical synthesized NLFM
The synthesized NLFM signal s(t) realizable in practice is the waveform with finite duration time, constantamplitude and continuous inner pulse frequency modulation. Its shape describes the formula as follows:
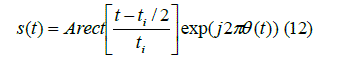image
where A — signal amplitude, i t — signal duration timeand θ(t) — the angle modulation function. Realizing the limit change from the parameters m and n integer set to the values interval from the real number set one can change from the case of frequency manipulation to the case of continuous frequency modulation.
D. Receiver-end processing and correlation
Received signal are process for detection of range (distance) and velocity. In receiver, signal is compressed in frequency domain which can be regarded as dual to pulse compression reduces time-bandwidth (TB) product of the signal. Distance is calculated from time delay and velocity from frequency shift by the effect of Doppler shifting. Pulse compression is obtained by cross-correlation of received signal with transmitted signal. The effect of delay on each code set is considered in such a way that all the cross-correlation peaks are lined up at a single point in time, which make analysis difficult. Figure shows optimum matched filter and correlation integration.
The receiver corresponding to the ith code will be analyzed. The receiver signal is given by
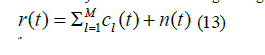image
Upon reception of r(t) at the receiver for ith code , decision variable is obtained by cross-correlation r(t) with matched filter normalized to unit energy.To get complete cross-correlation between the matched filter and code, we add the output of the pieces of the matched filter, 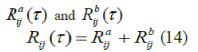image

IV. SIMULATION RESULT
Simulation was performed to compare different code set to improve the ambiguity function. The good code set contain good ambiguity function with single main-lobe and many peak side-lobes. Code set contain the combination of upchirp and down-chirp which are usually used in the radar, altimeter and communication fields. This stimulation helps to optimize the signal to noise ratio and spectral efficiency in the radar receivers. The figures also contain the instantaneous frequency plots corresponding to the 3D ambiguity functions for the types of codes being analyzed. A sample chirp ambiguity function is given below. While seeing the figure main amblitude and side lobes are close to each other. So this is not a good response to a recever with noise. The time side lobe should be maximum.In figure 6 shows the ambiguity function of PLFM with down-chirp up-chirp combination and triangular FM chirp codes [1].
If we convert to frequency-time plot the first plot is „V‟ shaped and second plot is „Λ‟, triangular FM chirp. Triangular shaped chirp has the ability to both tolerate and detector Doppler shifts because time side lobe levels are more.The proposed PNFM code set as shown in Figure 7 has superior ambiguity function with good time side lobe level. These types of code sets are better immune to jammer noise and good detection when used as radar receiver.When the instantaneous frequency plots corresponding to chirp code set gives a nonlinear frequency modulation of the signal. The time side-lobe level is good which is useful in radar like applications.
Time domain weighting is equals to the amplitude modulation of the transmitted signal. However such implementation will lead to reduction of transmitted power, and therefore a signal to noise ratio loss will occur. Frequency domain weighting spectrum shaping using well knows weighting windows such as Hann and Hamming [10]. However the implementation of weighting windows may lead to the penalty of main-lobe broadening. NLFM waveform is designed such that its matched filter response satisfies the side-lobe requirements. Since the receiver is matched with to the signal shape, no mismatch losses as in time domain weighting and frequency domain weighting [2].

V. CONCLUSION
Non-linear FM (NLFM) is becoming more practical use because of its various benefits such as inherently low range sidelobes which yields an advantage in SNR compared to Linear FM. In this paper compared PLFM and proposed with new class of PNFM. The 3D ambiguity function plots of the proposed PNFM are compared with those of NLFM codes. The main sidelobe to peak sidelobe ratio could be increased considerable, without using weighting function window. The PNFM code set proposed in this paper could be implemented as a digital code set for modern digital radar. Since the analysis relating to MCI is very pessimistic, it is suitable to use a stochastic method of analysis.

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4


Figure 5 Figure 6 Figure 7
Figure 5 Figure 6 Figure 7
 

References
  1. Farhan A. Qazi, Adaly T. Fam, “Good Code Set based on Piecewise Linear FM” IEEE 2012
  2. Chan, Y. K. and V. C. Koo, “Sidelobes Reduction Using Simple Two And Tri-Stages Non Linear Frequency Modulation (NLFM)”, Progress In Electromagnetics Research, PIER 98, 33-52, 2009
  3. Igor V. Komarov, Sergey M. Smolskiy, “Fundamentals of Short-Range FM Radar”, Artec House Publishers, 2003.
  4. Collins, T. and P. Atkins, “Nonlinear frequency modulation chirps for active sonar", IEE Proceedings - Radar, Sonar and Navigation, Vol. 146, No. 6, 312-16, Dec. 1999.
  5. Chan, Y. K. and V. C. Koo, “An introduction to synthetic aperture radar (SAR)", Progress In Electromagnetics Research B, Vol. 2, 27{60, 2008.
  6. Chan, Y. K. and S. Y. Lim, “Synthetic Aperture Radar (SAR) signal generation", Progress In Electromagnetics Research B, Vol. 1, 269{290, 2008.
  7. N. Levanon, E. Mozeson, “Radar Signals,” A John Wiley & sons, inc., Publication, 2004.
  8. Stefan Hengstler, Dayalan P. Kasilingam, Antonio H. Costa, “A novel chirp modulation Spread Spectrum Technique for Multiple Access,” IEEE 7th Int. Symp. on Spread-Spectrum Tech. & Appl., Prague, Czech Republif, Sept. 2-5, 2001.
  9. Doerry, A. W., “SAR processing with non-linear FM chirp waveforms", Sandia Report, Sandia National Laboratories, 2006.
  10. Barton, D.K., “Radar System Analysis and Modeling, Artech House”, ISBN 1-58053-681-6, Norwood, 2005.
  11. E. S. Kashani and Y. Norouzi, “Signal Processing for High Resolution RCS Measurement”, Progress In Electromagnetics Research Symposium Proceedings, KL, MALAYSIA, 747-751 March, 2012.
  12. Mohd. MoazzamMoinuddin, Mallikarjuna Reddy. Y., Pasha. I. A., Syed A. Naveed and Lal Kishore. K., “Multiple Target Detection for High Resolution Doppler Radar”IACSIT International Journal of Engineering and Technology, Vol. 3, No. 5, October 2011
  13. S. Haykin, “Optimal Waveform Design for Cognitive Radar” 42nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, California, October 2008.
  14. Bergin, J.S.; Techau, P.M.; Don Carlos, J.E.; Guerci, J.R.; , "Radar waveform optimization for colored noise mitigation," Radar Conference, 2005 IEEE International , vol., no., pp. 149- 154, 9-12 May 2005
  15. A.Kranthi, Ch.Srinivasu, “Performance Evaluation of Various Signal Processing Techniques in a Tracking Radar”, International Journal of Engineering Science and Technology (IJEST), ISSN : 0975-5462 Vol. 4 No.06 June 2012
  16. Woodward. P. M., „Radar ambiguity analysis‟, Technical note 731, Royal Radar Establishment, Malvern, England, UK, 1967.
  17. Skolnik, M., Introduction to Radar Systems, 3rd Edition, McGraw Hill, Boston, 2001.
  18. A.Kranthi, Ch.Srinivasu, “Performance Evaluation of Costas codes using Fusion Techniques”, International Journal of Scientific and Research Publications, Volume 2, Issue 7, July 2012 ISSN 2250 3153
  19. T.K. Bhattacharya and P.R.Mahapatra. “A Powerful Range-Doppler Clutter Rejection Strategy For Navigational Radars”, IEEE CH2759- 918910000-0132, 1989.
  20. David M. Pozar, Microwave Engineering, Third Edition, Wiley
  21. http://prod.sandia.gov/techlib/access-control.cgi/2006/065856.pdf
  22. J. A. Johnston, A. C. Fairhead, “Waveform design and Doppler sensitivity analysis for nonlinear FM chirp pulses”, IEE Proceed ings F (Communications, Radar and Signal Processing), Vol. 133, No. 2, p. 163-175, April 1986.
  23. D. P. Morgan, “Nonlinear chirp radar waveforms with improved tolerance to Doppler shifts”, IEE Colloquium on `Physics and Device Applications of Acoustic Waves' (Digest No.69), p. 8/1-5, London, UK, 22 May 1987.