ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
A. Pourhabib Yekta1, A. Khoshkenar2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this article power series method, as well-known method for solving ordinary differential equations, has been employed to solve linear systems of first order differential equations. Theoretical considerations and convergence of the method for these systems are discussed. Some examples are presented to show the ability of the method for such systems.
Keywords |
| Power Series Method, Linear Systems of Ordinary Differential Equations. |
INTRODUCTION |
| A linear system of first order differential equations can be considered, as: |
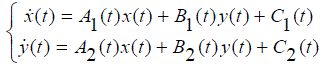 |
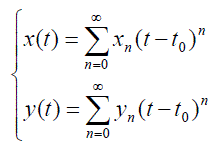 |
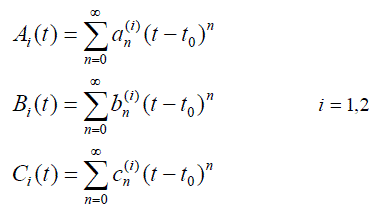 |
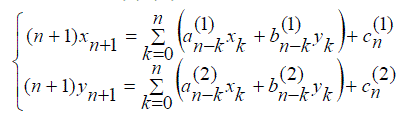 |
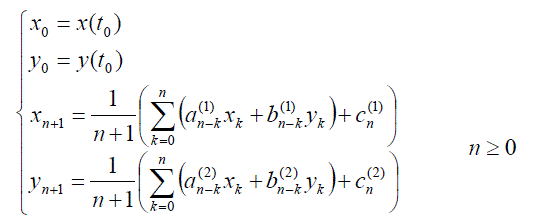 |
CONCLUSION |
| Power series method has been known as a powerful device for solving second order linear differential equations. Here we used this method for solving linear system of first order differential equations. The convergency of solutions has been shown. We present three examples and as it shown this method has the ability of solving such systems. |
ACKNOWLEDGEMENTS |
| We are extremely thankful and pay our gratitude to Islamic Azad University of Sowmesara for financially support on completion of this project in its presently. |
References |
|