International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Some Common Fixed Point Theorems in Cone Rectangular Metric Space under T – Kannan and T – Reich Contractive Conditions

M. Rangamma1, P. Mallikarjun Reddy2*
  1. Professor, Department of Mathematics, Osmania University, Hyderabad, Telangana, India
  2. Lecturer in Mathematics, Govt. Polytechnic for women (Min.), Badangpet, R.R. District, Telangana, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The purpose of this paper is to establish some common fixed point theorems for two self mappings which satisfy T- Kannan and T- Reich contractive conditions in cone rectangular metric space.

Keywords
cone rectangular metric space, common fixed point theorem, coincidence point, contractive condition.

INTRODUCTION
Recently, Huang and Zhang [5] introduced the notion of cone metric space. They have replaced real number system by an ordered Banach space and established some fixed point theorems for contractive type mappings in a normal cone metric space. The study of fixed point theorems in such spaces is followed by some other mathematicians; see [1], [5], [8], [11], [14]. In 2009, Azam, Arshad and Beg [2] extended the notion of cone metric spaces by replacing the triangular inequality by a rectangular inequality and they proved Banach contraction Principle in a complete normal cone rectangular metric space. Several authors proved some fixed point theorems in such spaces see; [6], [9], [10], [12], [15]. In 2009, Jleli, Samet [6] extended the Kannan‟s fixed point theorem in a complete normal cone rectangular metric space. In 2012, R. A. Rashwan and S. M. Saleh [12] extended Banach contraction principle in cone rectangular metric space with two self mappings and proved common fixed point theorem for T- contractive condition in cone rectangular metric space. In 2013, Malhotra et al. [10] generalized the result of Azam et al. [2] in ordered cone rectangular metric space and proved some fixed point results for ordered Reich type contractions. In this paper, we prove some common fixed point theorems for two self mappings which satisfy T – Kannan and T – Reich contractive conditions in cone rectangular metric space. Our results generalize and extend the results of M. Jleli et al. [6] and Malhotra et al. [10] on cone rectangular metric spaces.

PRELIMINARIES
First, we recall some standard definitions and other results that will be needed in the sequel.
image
image

MAIN RESULTS
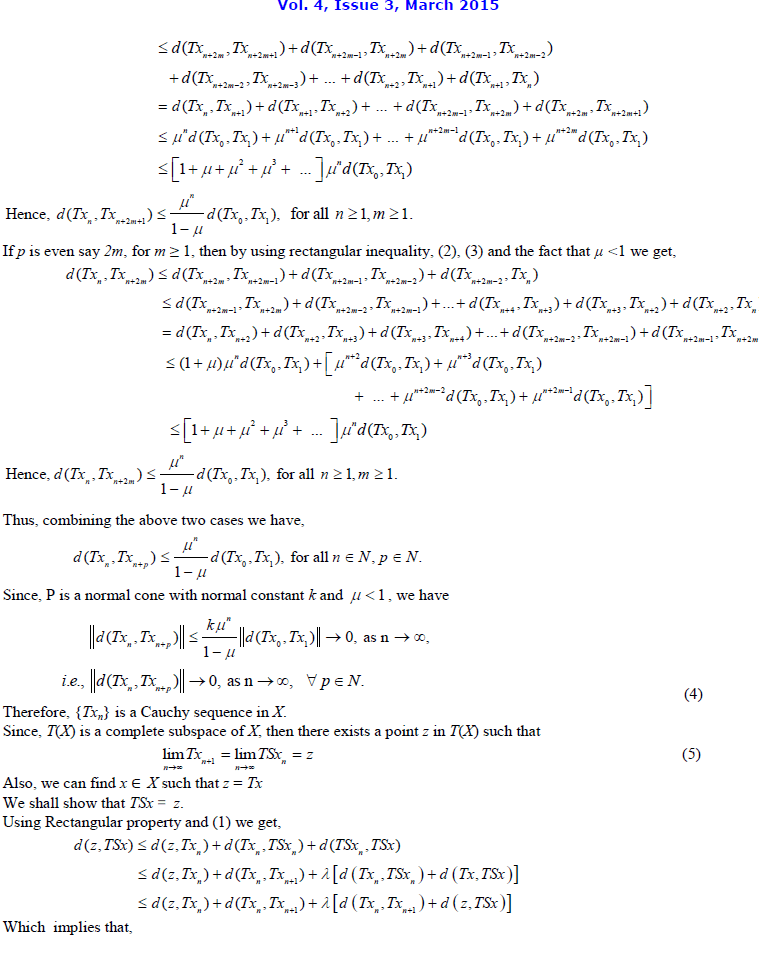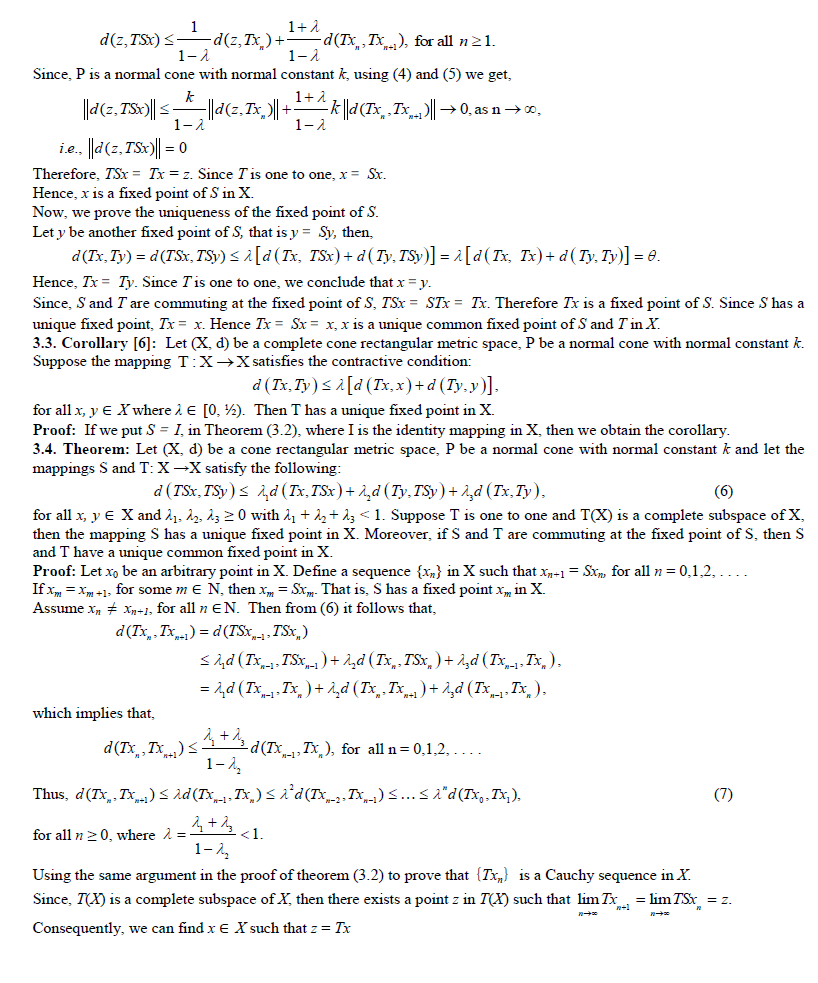image
image
image
image

CONCLUSION
In this article we have proved that the existence and uniqueness of common fixed point theorems for T-Kannan and TReich contractions in cone rectangular metric spaces. We note that the results of this paper generalize the results of M. Jleli et al. [6] and Malhotra et al. [10] on cone rectangular metric spaces.

References
  1. Abbas. M and Jungck. G, “Common fixed point results for non commuting mappings without continuity in cone metric spaces”, Journal of Mathematical Analysis and Applications, 341, 416–420, 2008.
  2. Azam. A, Arshad. M and Beg. I, “Banach contraction principle on cone rectangular metric spaces”, Appl. Anal.Discrete Math., 3, 236–241, 2009.
  3. Banach. S, “Sur les op´erationsdans les ensembles abstraits et leur application aux´ equations int´egrales”, FundamentaMathematicae 3(1), 133– 181, 1922.
  4. Beiranvand. A, Moradi. S, Omid. M and Pazandeh. H, “Two fixed point theorem for special mapping”, arXiv: 0903. 1504v1 [math.FA], 2009.
  5. Huang. L. G, Zhang. X, “Cone metric spaces and fixed point theorems of contractive mappings”, J. Math. Anal.Appl., 332, 1468–1476, 2007.
  6. Jleli. M, Samet. B, “The Kannan fixed point theorem in a cone rectangular metric space”, J. Nonlinear Sci. Appl., 2, 161-167, 2009.
  7. Kannan. R, “Some results on fixed point”, Bull. Calcutta Math.Soc. 60, 71 - 76, 1968.
  8. Malhotra. S. K, Shukla. S and Sen. R, “Some coincidence and common fixed point theorems in cone metric spaces”, Bulletin of Mathematical Analysis and Applications 4(2), 64-71, 2012.
  9. Malhotra. S. K, Sharma. J. B and Shukla. S, “g-weak contraction in ordered cone rectangular metric spaces”, The Scientific World Journal, 2013a.
  10. Malhotra. S. K, Shukla. S and Sen. R, “Some fixed point theorems for ordered reich type contractions in cone rectangular metric spaces”, ActaMathematicaUniversitatisComenianae (2), 165–175, 2013b.
  11. Morales. J. R and Rojas. E, “Cone metric spaces and fixed point theorems of T-Kannan contractive mappings”, Int. Journal of Math.Analysis, 4(4), 175–184, 2010.
  12. Rashwan. R. A, Saleh. S. M, “Some Fixed Point Theorems in Cone Rectangular Metric Spaces”, MathematicaAeterna, Vol. 2, no. 6, 573 – 587, 2012.
  13. Reich. S, “Some remarks concerning contraction mappings”, Canad. Nth. Bull. 14, 121 - 124,1971.
  14. Rezapour. S, Hamlbarani. R, “Some notes on paper Cone metric spaces and fixed point theorems of contractive mappings”, J. Math. Anal.Appl., 345 (2), 719–724, 2008.
  15. SatishShukla, “Reich Type Contractions on Cone Rectangular Metric Spaces Endowed with a Graph”, Theory and Applications of Mathematics & Computer Science 4 (1), 14–25, 2014.