ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Atul K Kukreti1, Shilpa Gupta2, Manish Saxena3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Antimony (Sb) based chalcogenides have an adequate potential in nonlinear and optoelectronic applications. In the present work, a new quaternary Se70 Ge10Te20-xSbx (x = 3, 6, 9, 12, 15, 18) system has been studied theoretically for various important physical parameters. The impact of variation of Sb (replacing Te) on the system has been discussed in terms of average coordination number, cohesive energy, heat of atomization, and theoretical optical band gap of the system. Almost all the parameters are found to vary linearly with the variation in Sb content.
Keywords |
| Quaternary Chalcogenide Glasses, Cohesive Energy, Heat of Atomization, Energy Gap. |
INTRODUCTION |
| Elements of group VI in periodic table (S, Se, and Te ) along with more electropositive element such as Sb form a special class of chalcogenide glasses. The phase change properties of chalcogenides make them attractive candidates to be used in all-optical devices [1-3], Chalcogen glasses are generally less weakly bonded materials than oxide glasses. The alloy of Se-Te improves the corrosion resistance and optical sensitivity of the alloy [4, 5]. The addition of Ge and Sb with Se-Te alloy makes the material more promising glasses having low transmission loss and high transparency to infrared radiations from 2 - 16 μm [6]. Ge-Se and Sb-Se glasses are promising materials for infrared optical fibres not only due to their high non-linearity and refractive index but also to their relatively good thermomechanical and chemical properties. The versatile behaviour of these materials makes us select this composition and study the effect of Sb in corporation in physical properties of Ge-Te-Se glass.. The addition of metallic impurity to glass alloy increases the conductivity and is very suitable for device fabrication [7, 8]. |
| The absence of long–range order of chalcogenide glassy semiconductors allows the modification of their optical properties to a specific technological application by continuously changing their chemical composition. Hence the study of the dependence of the optical properties on composition is important to improve technological Application. Te–based glasses find applications at longer wavelength in IR region such as CO2 infrared sensing at 15 μm and outer space life detection [9]. Te based glasses are suitable for integrated optics and optical storage due to high refractive index, photosensitivity and rapid amorphous– to–crystalline transformation [10]. |
| Another aspect in the studies of Ge–Sb–Se–Te alloys is the proximity of Sb and Te in the periodic table, which is the reason for Te and Sb to resemble each other. One has to be very careful in modelling because the small difference between Sb and Te sometimes cannot be distinguished. This problem represents still another reason to perform a systematic study across a family of alloys and to avoid basing conclusions on distinguishing between these atoms. In recent years the number of papers dealing with telluride glasses from systems, such as Ge–Sb–Te, Te–Sb–Se [10, 11, 12 ], are reflecting the growing interest in these materials. Nowadays the attention is extended over quaternary systems as possible candidates for optoelectronic applications. |
II. IONIC CHARACTER OF COVALENT BOND |
| According to Philips – Thorpe bond constraint theory for coordination number Z=2.4 all bonds are absolutely covalent. But for any other value of Z the covalent bonds have some ionic character .that is molecule becomes polar. The ionicity introduces a tendency towards ordering because of the non-directional character. Ionicity of a bond is calculated using the Pauling formula [13]. |
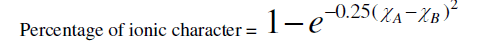 |
| where (χA-χB) is the difference in the electro negativities of atoms A and B. That, there should be a direct connection between bond strength and the glass formations was recognized by a number of investigators [14, 15]. High value of bond strength increases the glass forming tendency. Since chalcogenide glasses are made from materials such as sulphur, selenium, arsenic, germanium, and tellurium, which have predominantly covalent bonds, the degree of covalency in the bond of amorphous glass under investigation can be calculated by using the Pauling relationship as |
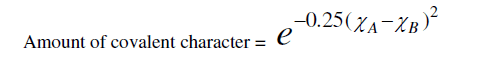 |
| Elements with more than 90% covalent character are more promising for glass formation. The chemical bonding related atomic parameters such as electro negativity and ionicity provides a mean for classify and understand many basic properties of materials [Table 1]. |
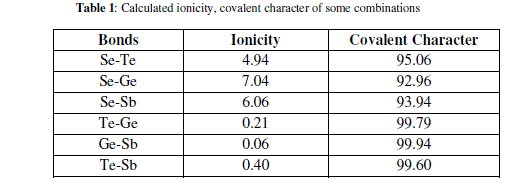 |
| Electro negativity has been defined differently by different investigators. Pauling defined electro negativity as the power of an atom or molecule to attract electron to it. Electro negativity of a composition is defined as the geometric mean of all the constituents forming a compound. The presence of Sb makes the alloy ionic in character. It is clear from the fig. 1 that values of electro negativity decreases from 2.405 to 2.397 with increase in concentration of Sb from 3 to 18 at %. |
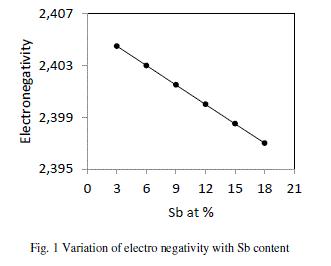 |
III. AVERAGE COORDINATION NUMBER |
| J. C. Phillips gave the mechanical-constraint counting algorithms to explain glass forming tendencies [16, 17]. The strongest covalent forces between nearest neighbours serve as Lagrangian (mechanical) constraints defining the elements of local structure (building blocks). Constraints associated with the weaker forces of more distant neighbours must be intrinsically broken leading to the absence of long-range order. The well known Phillips–Thorpe approach is based on comparing the number of atomic degrees of freedom with the number of inter-atomic force field constraints. If the number of degrees of freedom is greater than the number of constraints, the network is “floppy”; conversely, if the network becomes over-constrained, stressed-rigid structures will percolate throughout the entire network. According to Phillips, the tendency of glass formation would be maximum when the number of degrees of freedom exactly equals the number of constraints. For the composition Se70 Ge10Te20-xSbx (x = 3, 6, 9, 12, 15, 18), the average coordination number (Z) was calculated by using the standard method [18] |
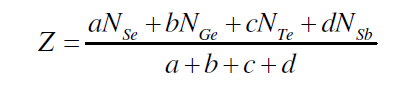 |
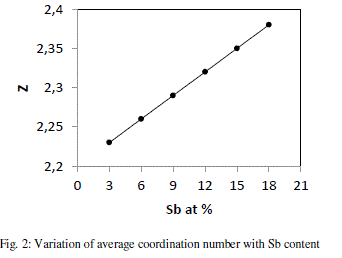
| where a, b,c and d are the at. % of Se, Ge, Te and Sb respectively and NSe(2), NGe(4), NTe(2) and NSb (3)are their respective coordination number [18]. The calculated values of average coordination number for system Se70 Ge10Te20- xSbx (x = 3, 6, 9, 12, 15, 18) are shown in fig. 2, from where it is clear that values of Z increase from 2.23 to 2.38 with increase in concentration of Sb from 3 to 18 at %. |
 |
IV. DEVIATION FROM THE STOICHIOMETERY OF COMPOSITION |
| The parameter R that determines the deviation from stoichiometry is expressed by the ratio of content bond possibilities of chalcogen atoms to that of non-chalcogen atoms. Se70 Ge10Te20-xSbx (x = 3, 6, 9, 12, 15, 18) system, the parameter R is given by [19, 20]. |
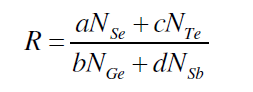 |
| where a, b, c, d are atomic frictions of Se, Ge, Te, and Sb respectively. The threshold at R=1 (the point of existence of only heteropolar bonds) marks the minimum selenium content at which a chemically ordered network is possible without metal–metal bond formation. For R>1, the system is chalcogen rich and for R<1, the system is chalcogen poor. |
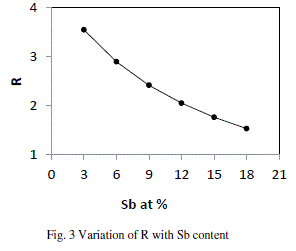 |
| From fig. 3, it is clear that our system is chalcogen rich and turning towards less chalcogen rich with the increase in content of Sb in the system, but still far away from being chalcogen poor. As the material is chalcogen rich and so having the high energy lone pair electrons leads to qualitative different electronic densities of state. The valence band is then non bonding and does not significantly contribute to the cohesive energy. The major limitation of this approach is that it does not account for molecular interactions, which play a vital role in the relaxation process in the glass transition region. |
V. COHESIVE ENERGY, AVERAGE HEAT OF ATOMIZATION AND ENERGY GAP |
| The cohesive energy of the system, defined as the stabilization energy of an infinitely large cluster of material per atom, has been calculated using the Chemical Bond Approach (CBA) [21]. According to CBA, atoms combine more favorably with atoms of different kind until all the available valences of the atom are filled. Bonds are always formed in the sequence of decreasing bond energies, which are assumed to be additive in nature. The heteropolar bond energies can be calculated by the relation [22], |
| where EA-A and EB-B are the homopolar bond energies and χ A and χ B are corresponding electro negativities. |
| The cohesive energy can be calculated using the relation [22], |
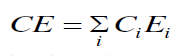 |
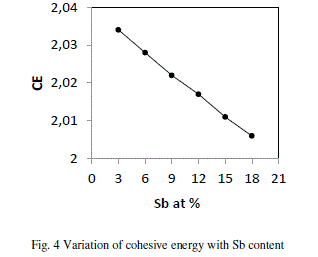
| where Ci is the distribution of the chemical bonds and Ei is the energy associated with the corresponding bonds From fig 4 it is evident that CE decreases with increase in Sb at. % from 3 to 18. Se atoms are strongly bonded to the Ge atoms and fill the available valences of the Te and Sb atoms respectively. But, still there are unsaturated Se atoms which appear as excess Se- Se bonds in the system. With increase in Sb (Bond energy 1.97 eV), Te decreases (bond energy 2.131 eV) so, Te-Se bonds concentration decreases Thus, the overall bond energy of the system decreases and hence the value of CE. |
 |
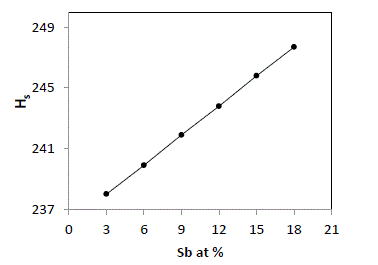
| The average heat of atomization, Hs, is defined as a direct measure of cohesive energy and can be calculated, in kcal/g/atom, for the quaternary system The average heat of atomization, Hs, is defined as a direct measure of cohesive energy and can be calculated, in kcal/g/atom, for the quaternary system Se70 Ge10Te20-xSbx [23]. The values of Hs were found to be increased from 238 to 247.7 with increase in concentration of Sb from 3 to 18, as depicted in fig. 5. |
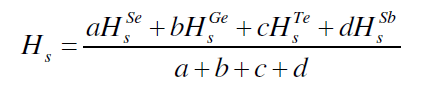 |
| Where a, b, c and d are the atomic % of Se, Ge, Te and Sb respectively. |
 |
| The band gap values may be correlated to the bond strength of the system. Average single bond energy (Hs/z) specifies the bond strength and it decreases with an increase in the Sb at. %. This decreases the bond strength of the system. The band gap values have been calculated using Shimakawa’s relation as [24], |
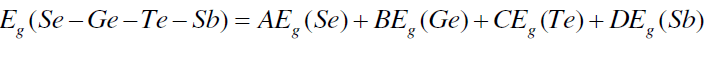 |
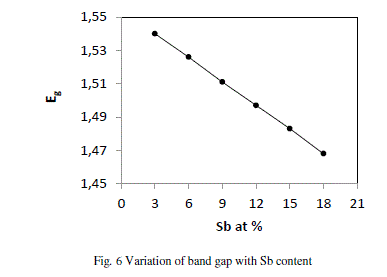
| where A, B, C, D are the volume fractions and Eg (Sb) = 0.101 eV, Eg (Se) = 1.95, Eg (Ge) = 0.95 eV and Eg (Te) = 0.65 eV are the energy gaps of Sb, Se, Ge and Te respectively. The variation of Eg with increase in content of Sb follows from the above discussion. Fig. 6 shows that values of Eg decrease from 1.540 to 1.468 with increase in concentration of Sb from 3 to 18 at %. |
 |
VI. CONCLUSIONS |
| The physical interpretations and their results make the composition Se70 Ge10Te20-xSbx as the most cross linked and a suitable one. The coordination number and heat of atomization increases because coordination number and heat of atomization of Sb are greater than that of Te. The stoichiometry R decreases due to decrease in contents of chalcogen Te and hence increases in content of Sb. It is concluded that an increase in antimony content decreases the electro negativity, stoichiometry (R), cohesive energy and optical band gap but increases the heat of atomization. |
References |
|