ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Sikander Azam*1, Wilayat khan1, Saleem Ayaz Khan1, A. H. Reshak1,2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The thermoelectric properties of Cu2ZnSnS4 and Cu2ZnSnSe4 are calculated by means of the semi-classical Boltzmann transport theory. The average values of electrical conductivity, thermal conductivity and Seebeck coefficient with two constant temperatures verses chemical potential are reported and discussed in detail. The Seebeck coefficient value recommends that both compounds are good for thermoelectric applications. We also investigated the electrical conductivity, thermal conductivity, Seebeck coefficient, power factor and the resistivity verses variable temperature. In which the maximum power factors are evaluated, suggesting that the compounds have good thermoelectric properties
Keywords |
| Effective mass, electrical conductivity, thermal conductivity and Seebeck coefficient |
INTRODUCTION |
| To decrease the use of fossil fuels, other energy sources such as solar energy should be developed. Solar cells are an interesting power source, because they do not generate harmful emissions. Among some solar cell components, the Sibased solar cell is the most broadly used worldwide. Although, it is necessary to develop non-Si-based solar cells due to a need of highly pure Si sources. Thus, we are developing new type of solar cell material, Cu2ZnSnS4 (CZTS) slim films [1,2]. CZTS thin films first formed the heterostructure apparatus by Ito [3]. CZTS thin films are an ideal material for reduced cost solar units because neither low metals nor harmful components are needed. Although the alteration efficiency of a CZTS solar cell is a few per hundred, which is lower than that of Si-based solar units (∼20%), there is an opportunity to advance the efficiency by better envisage of the materials. Along the advancement of growing high-quality complex materials, the group I2-II-IV-VI4 quaternary semiconductors have promptly been of wide interest due to numerous prospects in unpredictable the chemical composition, and thus optimizing the material utility. Particularly Cu2ZnSnS4 has obtained much consideration as being a promising nominee as absorber level in solar cell technologies [4-9], and devices have already come to a alteration efficiency of 6.7% (April 2008) [7]. Two primary thin film technologies founded on CdTe and Cu(In,Ga)(Se,S)2 (CIGS) have emerged in the past decades. The light-to-electricity conversion efficiencies of these devices have come to a grade close to 15%, which are nearly comparable to their Si counterparts [10]. Competence of thin film solar units prepared per year is about hundreds of MW. Although, the cost and shortage of In and Te, as well as the toxicity of Cd, will become foremost issues of their expansion to a GW scale [10]. Quaternary and quinary kesterites created of Cu- Zn-Sn S (Cu2ZnSnS4 (CZTS)), Cu-Zn-Sn-Se (Cu2ZnSnSe4 (CZTSe)), and their blended compound (Cu2ZnSn(S,Se)4 (CZTSSe)) are referents of the CIGS chalcopyrite compound, which are got by refurbishing trivalent indium (In) and gallium (Ga) with divalent zinc (Zn) and tetravalent tin (Sn). These direct band-gap p-type semiconductors have received much attention as promising candidates for reduced cost and non-toxic absorber layers for thin film solar cell [11]. So far, the best effectiveness of 11.1 % has been described for the CZTSSe-based solar cell made-up by spin-coating of hydrazine-based precutsor solutions pursued by annealing. This outcome illustrates the exciting potential of these kesterites for future functional applications. The thin film outcomes are very stimulating they may be most appropriate for small-scale electrical devices and optoelectrical devices applications where small heat burdens or low grades of power generation are more appropriate. To address large-scale refrigeration (home refrigerators) or power generation (automotive or developed applications) requirements, then higher performance bulk materials will have to be developed. For increasing the effectiveness of the thermoelectric energy alteration and the significance of a materials’ dimensionless figure of merit, ZT=ïÃÂóS2T/ïÃÂëïÃâ¬Ã¬Ã¯Ãâ¬Ã has been the most important ambition in energy research in the past decade, where the notation σ, S, T and ïÃÂë are the electrical conductivity, Seebeck coefficient, temperature and thermal conductivity, respectively. These possessions are frequently consistent which constrains the optimization of each component and of ZT. For instance, a high electric conductivity generally directs to reduced Seebeck coefficient and a high electrical devices contribution to a high thermal conductivity, both of which are detrimental for thermoelectric applications. From the last twenty years, newfangled stratagem have appeared on technology electrons and phonons to boost ZT such as through bigger remuneration from electron quantum incarceration and from phonon dispersion in nanostructures. The lattice thermal conductivity decrease has been illustrated in many nanostructured thermoelectric components. Though, augmentation of the thermoelectric power component or the electrical devices part of ZT remains a challenge. To the best of our acquaintance there is no inclusive work (experimental or theoretical) on the thermoelectric properties of Cu2ZnSnS4 and Cu2ZnSnSe4 has been accounted in the literatures. As a result, we contemplate that it would be valuable to execute such calculations using the full potential linear augmented plane wave (FP-LAPW) method within the modified Becke-Johnson exchange correlation potential to explore the thermoelectric properties. The FP-LAPW has been proven to be one of the most accurate methods for the computation of thermoelectric properties of solid within density functional theory (DFT). |
II. METHODOLGY |
| The calculations of band structure are carried out with a self consistent scheme by solving Kohn–Sham equations using the full potential linearized augmented plane wave (FP-LAPW) method within the modified Becke Johnson (MBJ) [12] potential in the framework of density functional theory (DFT) [13] using Wien2k codes [14]. For the transport calculations, non-shifted mesh with 3000 k points are used. The Kmax = 7/RMT (R is the smallest muffin-tin radius and Kmax is the cutoff for the plane wave) is the convergence parameter in which calculations stabilize and converge in terms of the desired charge e.g. less than 0.001e between steps. The values of other parameters are Gmax = 12 (magnitude of the largest vector in charge density Fourier expansion or the plane wave cut-off) and muffin-tin radii for Cu2ZnSnS4 (Cu2ZnSnSe4), which is nearly 2.29 (2.38) for Cu, 2.35 (2.46) for Zn, 2.31 (2.44) for Sn and 2.03 (2.11) for S (Se) a.u. The band structure was fitted using the semi classical theory of the Boltzman package [15], in sequence to attain the thermoelectric properties of Cu2ZnSnS4 (Cu2ZnSnSe4) compounds. In this package the transport properties are rooted in the rigid band approach to conductivity. The other calculated transport properties i.e. Seebeck coefficient, electrical conductivity, thermal conductivity, power factor and resistivity have been calculated verses the temperature. |
III. RESULTS AND DISCUSSION |
EFFECTIVE MASS |
| The effective mass is an amount that is utilized to simplify band structure by constructing an analogy to the behavior of a free element with that mass. For some reasons and some materials, the productive mass can be considered to be a simple constant of a material. In general, although, the value of effective mass depends on the purpose for which it is utilized, and can vary depending on a number of components. As it simplifies the more general band used, the electrical devices effective mass can be seen as a significant basic parameter that leverages discernable properties of a solid, encompassing everything from the efficiency of a solar cell to the pace of an integrated circuit. The performance of the electrical transport is furthermore evaluated based on the quasi-classical approach of effective mass approximation, where the mobility of the charge carriers is taken to be inversely proportional to their effective mass, such as electron effective mass or hole (heavy hole and light hole) effective mass. The primary aim of the current exertion is to compute the thermoelectric properties of Cu2ZnSnS4 and Cu2ZnSnSe4 and its disparity with carrier concentration. It is obligatory to approximate the effective masses of the carriers in assorted electron and hole pockets to accomplish this task. We have premeditated the mean effective mass of the carriers at the conduction and valence band edges by fitting the energy of the respective bands to a quadratic polynomial in the reciprocal lattice vector k ïÃÂò . The effective mass obtained from the band structure called effective band mass, was estimated in the one-bandapproximation from the curvature band at extreme points in k-space (usually Γ point); or in other words, parts of the band mass, i.e. conduction band minimum (CBM) or valence band maximum (VBM), were fitted by parabolic curves as |
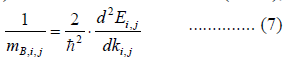 |
| Electron effective mass for Cu2ZnSnS4 (Cu2ZnSnSe4), is obtained from the curvature of the conduction band at Γ point of Brillouin zone. We have enlarged the band structures of Cu2ZnSnS4 (Cu2ZnSnSe4) as illustrated in Fig. 2. The intended effective masses for Cu2ZnSnS4 (Cu2ZnSnSe4) structure in some discerning directions of the Brillouin zone are given below. It is to certain extent apparent that the bands are less dispersive in the Cu2ZnSnSe4 structure approximately in all the high symmetry directions. This would entail large effective mass for the carriers belonging to these bands and hence a high thermopower. However, presence of carriers with large mobility is required for obtaining a higher electrical conductivity. Thus there is a opportunity of acquiring large ZT factor in materials possessing multiple pockets of carriers with large and small effective masses with the Cu2ZnSnSe4 one leading to large S, and the Cu2ZnSnS4 enhancing 0.0082 electron effective mass ratio. It is attention-grabbing to note that the electronic structure of both the Cu2ZnSnS4 (Cu2ZnSnSe4) structure exposes existence of multiple carrier pockets with significantly dissimilar effective masses thereby suggesting that they may be having good thermoelectric properties. The value of calculated electron effective mass ratio m*/me for Cu2ZnSnS4 (Cu2ZnSnSe4) in Γ direction is 0.0082 (0.0057). We also calculated effective mass ratio of the heavy holes mhh*/me for Cu2ZnSnS4 (Cu2ZnSnSe4) 0.0193 (0.0152) and light holes mlh*/me for Cu2ZnSnS4 (Cu2ZnSnSe4) 0.0147 (0.0141) for the investigated compound in Γ directions. THERMOELECTRIC PROPERTIES The difference in temperature between dissimilar materials induces thermoelectric voltage. In the Seebeck effect, this temperature difference produces a voltage of several microvolts per Kelvin between two materials. The Seebeck coefficient (SC) is expressed in units of (V/K). The sign of the thermo-power can determine the charged carriers which dominate the electric transport in the material. The SC is calculated from the following relation: |
| A larger induced thermoelectric voltage, for a given temperature gradient, will lead to a higher efficiency. Ideally, one would like very large thermopower values since only a small amount of heat is necessary to create a large voltage. A high quality thermoelectric material should have elevated electrical conductivity to minimize the Joule heating, small thermal conductivity to avoid thermal shorting, and elevated SC for greatest conversion of heat to electrical power. Semiconductors are ideal thermoelectric devices because of their band structure and electronic properties at high temperatures. Fig. 1 illustrates the transport properties versus chemical potential at two different temperatures. While the magnitude of the Seebeck coefficient (Fig. 1b) is reduced with increasing temperature at a certain chemical potential, the electrical conductivity over relaxation time (σ/τ) (Fig. 1b) is decreasing while the electronic thermal conductivity over relaxation time (kÃÂä /τâÃâÃâ) (Fig. 1c) increases with increasing temperature in the displayed chemical potential range. To calculate systematically the temperature dependent properties a series of transport properties verses chemical potential curves were calculated by varying the temperature by 400 K increments. After obtaining the chemical potential at a specific temperature from eq. (1), one can determine the values of S, σ/τ and kÃÂä /τâÃâÃâ at that temperature from the corresponding curve. Thermoelectric properties are capable of converting heat directly into electricity. They are based on the Seebeck effect discovered by Thomas Johann Seebeck in 1821. In Fig. 1b, the calculated Seebeck coefficients are plotted. The chemical potential dependence on the electrical transport properties of Cu2ZnSnS4 (Cu2ZnSnSe4) compounds was calculated at two different temperatures 300 k and 700 k as shown in the Fig. 1b. Within the rigid-band shift model, the chemical potential μ determine the carrier concentration of the compound. The Seebeck coefficients are positive in both compounds in the investigated temperature range, signifying hole-type carriers to the heat transport in these materials. As we increased the temperature from 300 K to 700 K the peaks of the Seebeck coefficient increases, whereas when we substitute S by Se all the peaks of Seebeck coefficient are decreases. Within the framework of the Boltzmann transport equation the electrical conductivity (σ) is expressed in the form of the ratio σ/τ, where (τ) is the relaxation time approximation. To calculate the electrical conductivity σ, we must determine the relaxation time τ. We assume that the relaxation time τ is direction independent, and treat relaxation time as a constant at a certain specific temperature and carrier concentration. Fig. 1a shows the calculated electrical conductivity. The results follow the trend that the electrical conductivity increases with increasing temperature but when we replace S by Se the conductivity decreases which exhibits metal-like behavior. To obtain σ and kÃÂä , âÃâÃâone needs to know the relaxation time τ. From σ/τ values, we obtained a set of the temperature dependent relaxation time as shown in Fig. 1a. The relaxation time shows that the increasing (decreasing) trend with increasing the temperature due to the increases (reduction) of mobility at the higher temperature. As we see that by increasing the temperature the conductivity of the investigated material increases (decreases). In metals thermal conductivity approximately tracks electrical conductivity according to the Wiedemann-Franz law [16], the freely moving valance electron is not only transferring the electric current but also heat energy. However, the general correlation between electrical and thermal conductance does not hold for other materials, due to the increased importance of phonon carriers for heat in non-metals. Thermal conductivity is imperative in material science, research, electronics, building insulation and related fields, particularly where high operating temperatures are achieved. High energy generation rates within electronics or turbines require the use of materials with high thermal conductivity. The thermal conductivity, ïÃâ¬Ã¨k ïÃâ¬Ã©, indicates the ability of a material to conduct heat for both; electronic and lattice contributions. So the thermal conductivity of a material is the sum of its electronic and the corresponding lattice thermal conductivities. In Fig. 1, we show the observed thermal conductivity ïÃâ¬Ã¨k ïÃâ¬Ã© for the studied Cu2ZnSnS4 (Cu2ZnSnSe4) compounds. The temperature characteristic of thermal conductivity of Cu2ZnSnS4 (Cu2ZnSnSe4) compounds exhibits the most peculiar features in all measured thermoelectric properties. Fig.1, shows that as we increase the temperature from 300 K to 700 K the thermal conductivity increases. This shows that the investigated material has not good electrical properties. Correspondingly materials of high thermal conductivity are widely used in heat sink applications and materials of low thermal conductivity are used as thermal insulation. Thermal conductivity of materials is temperature dependent. |
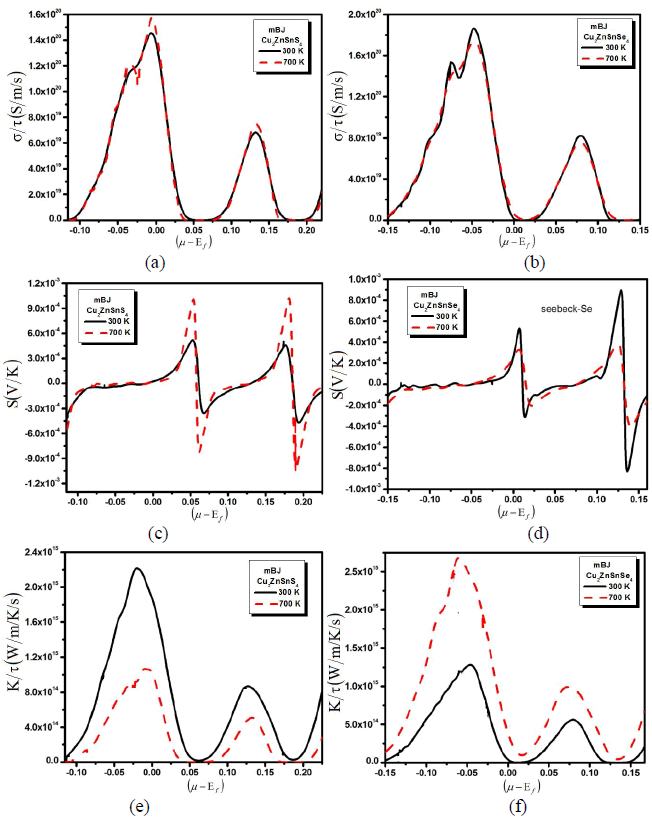 |
| Fig. 1: (a) Electrical conductivity, (b) seebeck beck coefficient and (c) thermal conductivity verses chemical potential with two constant temperatures. |
| We also calculated the transport properties verse the variable temperature in Fig. 2 (a,b,c,d and e). The calculated electrical conductivity verses temperature for both compounds has been plotted in Fig. 2a. The calculated spectra show that with the increase in temperature the conductivity of the material also increased and reaches to its maximum at 800 K. The increase in the electrical conductivity means that there are greater concentrations of carriers. |
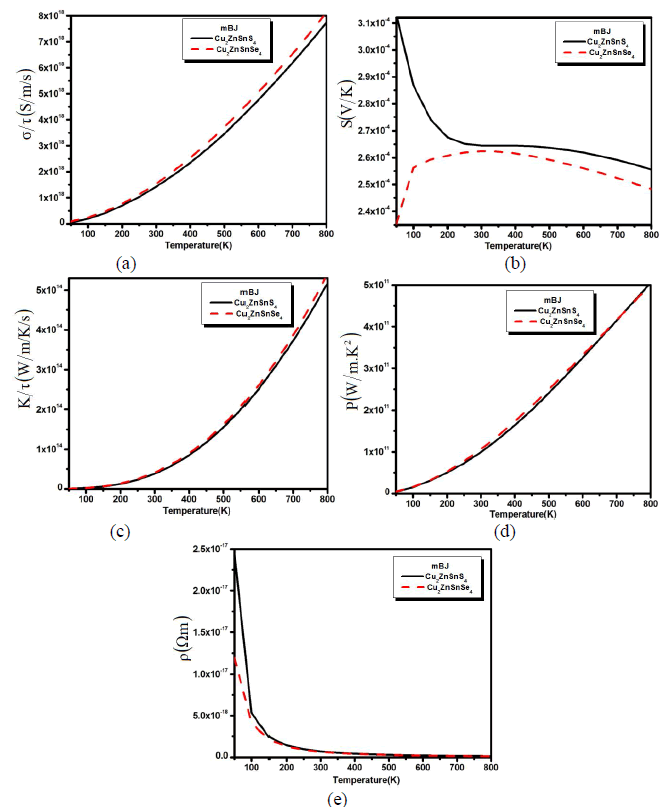 |
| Fig. 2: (a) Electrical conductivity, (b) thermal conductivity and (c) seebeck beck coefficient (d) power factor and (e) resistivity verses temperature. From Fig.2a we confirmed that the electrical conductivity is greater at higher temperatures, which shows that the electron is thermally excited to the conduction bands. The calculated Seebeck coefficient (S) of Cu2ZnSnS4 and Cu2ZnSnSe4 as a function of temperature is shown in Fig. 2b. This has a large p-type Seebeck coefficient. The magnitude of the Seebeck coefficient decrease up to 250 K and then maintains an equilibrium state till the 500 K and beyond the 500 K there is also a little decrease. But when we substitute S by Se, the behave of Seebeck coefficient curve for Cu2ZnSnSe4 becomes the reverse of Cu2ZnSnS4 curve (Fig. 2b). One can see that the Seebeck coefficient increases for Cu2ZnSnSe4 compound and decreases for Cu2ZnSnS4 with increasing the temperature till 300 K. Then above 300 K (450 K) the Seebeck coefficient of Cu2ZnSnSe4 (Cu2ZnSnS4) decreasing with increasing the temperature. This gradual decrease (increase) of the Seebeck coefficient is due to the thermal excitation (de-excitation) of electrons across the band gap. Holes are being the majority carriers are consistent with their higher mobility and smaller effective mass than the electron carriers. However, it is visible from Fig. 2b that the S falls rapidly than σ (see Fig. 2a), which illustrates the bipolar effect which take place when many bands contribute to carrier transport and is mostly strong in electron and hole band. This conduction (holes) radically reduces the Seebeck coefficient because the holes carry the opposite charge from electrons. This effect will also increase the thermal conductivity spectra which have been also calculated for Cu2ZnSnS4 (Cu2ZnSnSe4) as plotted in Fig. 2c. The Seebeck coefficient is not the only number that determines the usefulness of a material in a thermoelectric generator or a thermoelectric cooler. Under a given temperature coolness, the ability of a material to produce useful electrical power is quantified by its power factor, PF=S2ïÃÂóïÃâ¬Ã¬Ã¯Ãâ¬Ã where S is Seebeck coefficient and σ is the electrical conductivity. Material with high power factor is able to generate more energy in a space-constrained application, but they are not necessarily efficient. Fig. 2d shows the temperature dependent power factor which increases monotonically within the whole temperature range. The value increases rapidly above 300 K and followed with an almost linear increase till 800 k. The large power factor was obtained in the cases of low electrical resistivity. From the PF spectra it is clear that both materials shows good thermoelectric behavior at higher temperature. The calculated spectra for the resistivity have also been calculated as shown in Fig. 2e. The resistivity for both the compounds drops rapidly with increasing temperature below 300 K indicating a semiconducting behavior. At low temperature Cu2ZnSnS4 has greater resistivity than Cu2ZnSnSe4. |
IV. CONCLUSION |
| We investigate the transport properties of Cu2ZnSnS4 and Cu2ZnSnSe4. The transport properties were calculated using the Boltzmann transport theory within full potential linear augmented plane wave (FPLAPW) method based on DFT. The exchange correlation energy was solved with modified Becke Johnson. The average value of tensor components of electrical conductivity, thermal conductivity and Seebeck coefficient were conversed in detail. The gradual decrease (increase) of the Seebeck coefficient is due to the thermal excitation (de-excitation) of electrons across the band gap. Holes are being the majority carriers are consistent with their higher mobility and smaller effective mass than the electron carriers. The spectra of S falls rapidly than σ which illustrates the bipolar effect which take place when many bands contribute to carrier transport and is mostly strong in electron and hole band. From the power factor study we confirm that that both materials shows good thermoelectric behavior at higher temperature. |
ACKNOWLEDGMENT |
| The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, co-funded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI programme. |
References |
|