ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R.Thamaraiselvan1, S.Gopikrishnan2, V.Pavithra Devi3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Local algorithms determine the status (forwarding/non forwarding) of each node proactively based on local topology information and a globally known priority function. In this paper, we first show that local broadcast algorithms based on the static approach cannot achieve a good approximation factor to the optimum solution (an NPhard problem). However, we show that a constant approximation factor is achievable if position information is available. In the dynamic approach, local algorithms determine the status of each node “on-the-fly” based on local topology information and broadcast state information. Using the dynamic approach, it was recently shown that local broadcast algorithms can achieve a constant approximation factor to the optimum solution when (approximate) position information is available. However, using position information can simplify the problem. In some applications it may not be practical to have position information. Therefore, we wish to know whether local broadcast algorithms based on the dynamic approach can achieve a constant approximation factor without using position information.
Keywords |
| Local Broadcast Algorithm, CDS, Static approach, Dynamic approach. |
INTRODUCTION |
| Wireless ad hoc networks have emerged to support applications, in which it is required/desire to have wireless communications among a variety of devices without relying on any infrastructure or central management. In ad hoc networks, wireless devices, simply called nodes, have limited transmission range. Therefore, each node can directly communicate with only those within its transmission range and requires other nodes to act as routers in order to communicate with out-of-range destinations. One of the fundamental operations in wireless ad hoc networks is broadcasting, where a node disseminates a message to all other nodes in the network. . This can be achieved through flooding. Not every node is required to forward/transmit the message in order to deliver it to all nodes in the network. A set of nodes form a Dominating Set (DS) if every node in the network is either in the set or has a neighbour in the set. A DS is called a Connected Dominating Set (CDS) if the sub graph induced by its nodes is connected. Clearly, the forwarding nodes, together with the source node, form a CDS. On the other hand, any CDS can be used for broadcasting a message (only nodes in the set are required to forward). In this paper we show that, using only local topology information and a globally known priority function, the local broadcast algorithms based on the static approach are not able to guarantee a good approximation factor to the optimum solution (i.e., MCDS). On the other hand, we show that local algorithms based on the static approach can achieve interesting results such as a constant approximation factor and shortest path preservation if the nodes are provided with position information. In the dynamic approach, the status of each node (hence the CDS) is determined “on-the-fly” during the broadcast process. |
II. SYSTEM MODEL AND ASSUMPTIONS |
| We assume that the network consists of a set of nodes V, |V| = N. Each node is equipped with Omni directional antennas. Every node u ∈ V has a unique id, denoted id (u), and every packet is stamped by the id of its source node and a nonce, a randomly generated number by the source node. For simplicity, we assume that all nodes are located in two dimensional space .However, all the results presented in this paper can be readily extended to three-dimensional ad hoc networks. To model the network, we assume two different nodes u ∈ V and v ∈ V are connected by an edge if and only if |uv|=R, where |uv| denotes the Euclidean distance between nodes u and v and R is the transmission range of the nodes. Thus, we can represent the communication graph by G (V,R),where V is the set of nodes and R is the transmission range. This model is, up to scaling, identical to the unit disk graph model, which is a typical model for two-dimensional ad hoc networks. In reality, however, the transmission range can be of arbitrary shape as the wireless signal propagation can be affected by many unpredictable factors. Finally, we assume that the network is connected and static during the broadcast and that there is no loss at the MAC/PHY layer. These assumptions are necessary in order to prove whether or not a broadcast algorithm can guarantee full delivery. |
III. BROADCASTING USING THE STATIC APPROACH |
| Let the k-neighbourhood of a node u, denoted G(u),be the sub graph induced by u and nodes at most k hops away from u. Suppose each node is given a globally Pr(id(w),Gh(w)) which gets a nodeâÃâ¬ÃŸs id , id(w), and its local topology information, Gh(w) as inputs and returns a real number that determines the priority of w. For example, priority of a node can be determined by its id , by its degree (i.e. the number of its 1-hop neighbours) or by its neighbour connectivity ratio (i.e. ratio of pairs of neighbours that are not directly connected to all possible pairs of neighbours). In local broadcast algorithms based on the static approach, the status (forwarding/non-forwarding)of each node u, Stat(u), is a function of id(u), Gh(u) and Pr(id(v),G (v)), where v ∈ Gh(u) and the parameters h and hâÃâ¬ÃŸ. Note that the status of each node does not depend on that of other nodes. Therefore, any local topology change can only affect the status of the nodes in the vicinity. In designing local broadcast algorithms, we are looking for status functions that not only guarantee constructing a CDS (hence full delivery) but also ensure that the constructed CDS has small size, preferably within a constant factor of the optimum. In the following, we show that no such status function exists. The idea is to Gh(.), and the relative priority of the nodes in Gh(.) are the same. Without loss of generality, we can assume R =1. |
 |
| The approach of network partitioning to use geographical information has been used for different purposes including saving energy in sensor networks, and handling mobility in broadcast algorithms for ad hoc networks. In the primary work by Xu , the authors propose an algorithm that partitions the network area into square cells. To save energy, at each time, the algorithm selects one node in each cell as active and puts other nodes in the cell to sleep. The set of active nodes must form a CDS in order to maintain network connectivity and coverage. To guarantee this, the proposed algorithm in assumes that the side length of each square cell is R/√5, where R is the radio transmission range. . In this section, we show under what conditions the set of nodes constructed by selecting one node in each non-empty set form a CDS. We also show that these conditions can be relaxed at the price of selecting more than one yet a constant number of nodes in some non-empty cells. Therefore, the result of this section can be used to extend the work in to the case where some cells may contain no (working) sensor due to, for example, a non-uniform distribution of sensors, sensor mobility or sensor failure. Authors use a network partitioning approach in designing broadcast protocols for dense mobile ad hoc networks. To handle mobility, the proposed broadcast protocols in rely on the distribution of nodes as opposed to the majority of existing broadcast protocols that rely on the frequently changing communication topology. In this section, we focus on reducing the number of transmissions in a general static ad hoc network. Readers may refer to for a discussion on how to handle mobility when network partitioning is used. Theorem 1: Let α>0 and m ≥1 be constant numbers. Let S be a CDS. Suppose there are at most m nodes of S in any square of size αR× αR. |
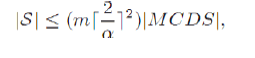 |
| Let α be a positive real number. Let Ssq(α) denoted a set constructed by dividing the network area into small square cells of size αR × αR and selecting exactly one node in each non-empty cell. As explained earlier, Let a be a positive real number. the set Ssq(α) is a dominating set (DS) if α ≤√2/2. Therefore, we use the notation DSsq(α) instead of Ssq(α),wherever α≤ √2/2. In general, the graph induced by DSsq (α) is not connected even for small values of α. Nevertheless, it can be proven that the graph induced by DSsq(α) is connected . if the network satisfies any of the two conditions that we call high-connectivity condition and high-transmission condition. Theorem 2: Let α, 0 <α≤1-c/2√2, be a real number. Note that α ≤√2/2.Let DSsq(α) be a constructed DS by selecting one node in each non-empty set. If G (V,cR) is connected, then DSsq(α) is a CDS whose size is at most [2/α]2|MCDS|. Theorem 3: Let α, 0 <α≤ min (2,c)/2√2, and c>0 be real numbers. Note that α≤√2/2. .Let DSsq(α) be a constructed DS by selecting one node in each non-empty set. If every node in DSsq(α) increases its transmission range to at least (1 + c)R, then DSsq(α) will be CDS whose size is at most[2/α]2 |MCDS| There are optimization techniques to further reduce the size of a constructed DSsq(α) or to relax the requirement of transmitting at higher power for many selected nodes. For example, suppose that node us is the selected node in cell Ci. The node us is not required to increase its transmission power if every node v within transmission range of any node u ∈ Ci within the transmission range of either us . |
 |
IV. BROADCASTING USING THE DYNAMIC APPROACH |
| Using the dynamic approach, the status (forwarding/non forwarding) of each node is determined “on-the-fly” as the broadcasting message propagates in the network. A. The Proposed Local Broadcast Algorithm Suppose each node has a list of its 2-hop neighbours this can be achieved in two rounds of information exchange. The proposed broadcast algorithm is a hybrid algorithm; hence every node that broadcasts the message may select some of its neighbours to forward the message. In our proposed broadcast algorithm, every broadcasting node selects at most one of its neighbours. A node has to broadcast the message if it is selected to forward. Other nodes that are not selected have to decide whether or not to broadcast on their own. This decision is made based on a self-pruning condition called the coverage condition. Algorithm 1: The proposed hybrid algorithm executed by u |
 |
 |
| B. Analysis of the Proposed Broadcast Algorithm Theorem 4: Algorithm 1 guarantees full delivery. Proof: Every node broadcasts a message at most once. Therefore, the broadcast process eventually terminates. By contradiction, assume that node d has not received the message by the broadcast termination. Since the network is connected, there is a path from the source node s (the node that initiates the broadcast) to node d. clearly ,We can find two nodes u and v on this path such that u and v are neighbours has received the message and v has not received it. The node u has not broadcast the message since v has not received it. Therefore, u has not been selected to broadcast; thus the coverage condition must have been satisfied for u. As the result, v must have a neighbour w, which has broadcast the message or selected to broadcast. Note that all the selected nodes will eventually broadcast the message. This is a contradiction as, based on the assumption, v cannot have a broadcasting neighbour. C. The Strong Coverage Condition As proven, the proposed broadcast algorithm guarantees that the total number of transmissions is always within a constant factor of the minimum number of required ones. However, the number of transmissions may be further reduced by slightly modifying the broadcast algorithm. As explained earlier, in the proposed algorithm, a selected node has to broadcast the message even if its coverage condition is satisfied. For example, a selected node u can abort transmission (by removing the message from the queue) at time t if by time t and based on its collected information, all its neighbours have received the message. D. Extending the Network Model The results presented in the paper can be extended to the case where the nodes are distributed in three-dimensional space. In other words, when the nodes are distributed in three dimensions it can be shown that local broadcast algorithms based on the static approach can provide a constant approximation if nodes have their position information. By replacing circles with balls, it can be similarly shown that Algorithm 1 can provide both full delivery and a constant approximation to the optimum solution. |
V. EXPERIMENTAL RESULTS |
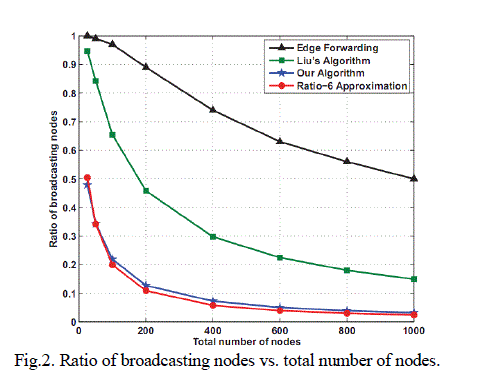
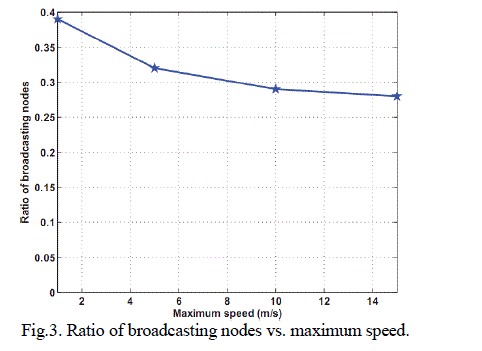
| One of the major contributions of this work is the design of a local broadcast algorithm based on the dynamic approach (Algorithm 1) that can achieve both full delivery and a constant approximation factor to the optimum solution without using position information. To confirm the analytical results, we implemented Algorithm 1, LiuâÃâ¬ÃŸs algorithm (a neighbour designating algorithm) [4], edge forwarding algorithm (a self pruning algorithm) [2] and According in the network simulator ns-2 and evaluated the ratio of broadcasting nodes (i.e., number of broadcasting nodes/total number of nodes) and end-to-end delay for each algorithm. Table I summarizes the parameters used in the ns-2 simulator. We also implemented the Wan-Alzoubi-Frieder algorithm [5] in C++ and used it as an approximation of the minimum number of broadcasting nodes required. Note that the Wan-Alzoubi-Frieder algorithm (referred to as ratio-6 approximation algorithm) is not a local algorithm and is only used as a benchmark as it has an approximation factor of at most 6 [7]. To compute the number of broadcasting nodes, we uniformly distributed the nodes in a square of size 1000×1000m2. We allowed only one network-wide broadcast at each simulation run, selected the next forwarding node randomly, and used the strong coverage condition in Algorithm 1 to further reduce the total number of transmissions. Fig 2 and 3 shows the average ratio of broadcasting nodes for over 500 runs for each given value of the input (i.e., the total number of nodes or the transmission range). To get the results shown in Figure 3, we set the transmission range to 250m and varied the total number of nodes from 25 to 1000. In Figure 4, the number of nodes was fixed to 1000 and the transmission range was varied from 50m to 300m. The transmission range and the total number of nodes were selected from a large interval so that the simulation covers very sparse and very dense networks as well as the networks with large diameters. |
 |
 |
VI. CONCLUSIONS |
| Local broadcast algorithms based on the static approach cannot guarantee a small sized CDS if the position information is not available. So we can introduced hybrid algorithm in dynamic approach using this algorithm we reduced number of transmissions and each node do self pruning so we reduced data redundancy so broadcast buffering time also reduced so compare to other algorithm our algorithm reduced the time complexity. The results presented in the paper can be extended o the case where nodes are distributed in three dimensional spaces. |
References |
|