Web Log Clustering using FCM and Swarm Intelligence Based Algorithms

Abstract

Clustering is the approach in which it groups data items having similar properties or behavior. This paper describes most representative techniques such as fuzzy c-means, FCM ant colony optimization as well as FCM particle swarm optimization for accurate results to overcome the limitations of traditional clustering techniques. The experimental result shows how these techniques are accurate and effective to search better cluster centers in Web usage mining.

Keywords

Fuzzy C-means, Particle swarm optimization, Ant colony optimization, clustering

INTRODUCTION

Data clustering is the process of finding similarities in data and putting similar data into groups and dissimilar data items into another group. Clustering is helpful whenever there is huge amount of data. Several clustering techniques are used on web log data but a traditional clustering technique has lot of limitations. Our paper shows how fuzzy c-means (FCM), FCM- Ant colony optimization (ACO), FCM-Particle swarm optimization (PSO) are better.

In the traditional clustering the samples are classified in the unique cluster which is hard clustering. One main limitation of classical clustering algorithm is that the numbers of clusters are known. However this is unsupervised clustering algorithm in which the number of clusters may not be known .Its aim is to determine the correct number of clusters without any prior knowledge about it. Although the fuzzy c- means algorithm produces good results still it is difficult to find optimal number of clusters within the dataset. The most widely used fuzzy clustering algorithm is fuzzy c-means introduced by Dunn in 1973 and later in 1981 by Bezdek. It uses iterative process that repeatedly iterates the cluster centres to exact location within data set. It is based on the initial centroids selected means all data points are calculated as the centroids of a cluster and assigns weightht by their degree corresponding to the clusters [1]. Particle swarm optimization (PSO) was introduced by Eberhart and Kennedy. PSO is based on social behaviour of birds, bees or school of fishes.

The main aim of our work is to form clusters with high accuracy. The proposed work involves grouping of IP address, session, user, date, time and page on web log data.

II. CENTROID BASED CLSTERING

The center based clustering is more efficient for clustering large datasets. In this each data item is placed in the cluster whose corresponding cluster center is shorter or closer. Center is nothing but it is representative of a clusters. K-means, Fuzzy c-means are most popular methods of centroids based clustering.

A. Fuzzy c- means

Fuzzy c-means is a method of clustering which allows one piece of data to belong to two or more clusters. It is based on minimization of objective function. Fuzzy c-means clustering involves two processes: the calculation of cluster centers and the assignment of points to these centers using a form of Euclidian distance. This process is repeated until the cluster centers stabilize.[4]. It assigns a membership value to the data items for the clusters within a range of 0 to 1. So it incorporates fuzzy set?s concepts of partial membership and forms overlapping clusters to support it.The algorithm calculates the membership value μ with the formula,

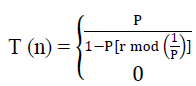Where,

μj(xi):is membership of xi in the jth cluster

dji :is the distance of xi in cluster cj

m: is the fuzzification parameter

p: is the number of specified cluster

dki: is the distance of xi in cluster ck

The new cluster centres are calculated with these membership values using the expression (4) as shown below

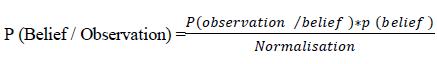Where,

cj: is the centre of the jth cluster

xi: is the ith data point

μj: is the function which returns membership value

m: is the fuzzification parameter

B. Fuzzy C-Means Algorithm

Initialize p=number of cluster

Initialize m=fuzzication parameter

Initialize Cj (Cluster centers)

Repeat

For i=1 to n: Update μj(xi) applying (3)

For j=1 to p: Update Cj with (4) with current μj(xi)

Until Cj estimate stabilize

This is a special form of weighted average. We modify the degree of fuzziness in xi?s current membership and multiply this by xi. The product obtained is divided by the sum of the fuzzified membership. The first loop of the algorithm calculates membership values for the data points in clusters and the second loop recalculates the cluster centres using these membership values. When the cluster centre stabilizes (when there is no change) the algorithm ends.

III. SWARM INTELLIGENCE

A. Ant Colony Optimization

ACO is proposed by Macro Dorigo in 1992. ACO is probabilistic technique which is inspired by the behavior of ants in finding paths from colony to food. The ACO is meta-heuristic inspired by the behavior of some special of ants that are able to find optimal path.

B. Fuzzy Ant Colony Optimization Algorithm

Step 1: Normalize feature values between 0 and 1

Step 2: Initialize the ants with random values with random two directions as positive and negative. When ants move from 0 to 1 then there is positive direction and when ants move from 1 to 0 in feature space then it consider as negative direction.

Step 3: For every „n? iterations, for all ants with probability Prest the ant reset for n iterations.

Step 4: If ant is not resetting then with a probability Pcontinue the ants continue in the same direction in feature space otherwise it changes its direction.

Step 5: If current partition is better than any of previous partition in ant memory then ant remembers current partition

Step 6: Else the ant with given probability goes back to better partition or continues from current partition.

After fixed number of iterations the ants stop.

C. Partical Swarm Optimization

Particle Swarm Optimization (PSO) is an evolutionary computation technique introduced by Kennedy and Eberhart in 1995. This algorithm is initialized with a population of random solutions known as particles. Each particle moves in feature space with a velocity that is dynamically adjusted. These dynamic adjustments are based on the historical behaviors of itself and other particles in the population. Each particle keeps track of its coordinates in the feature space which is associated with the best solution (fitness) it has achieved known as pbest. Another best value is tracked called gbest value. Fitness of all instances of generated clusters is calculated as lbest.

D. Particle Swarm Optimization Algorithm

P x: Dataset to be clustered

N: Number of clusters

S: Small positive valued constant

V: Random Velocity

Step 1: For dataset x, set initial random cluster vector <C1, C2,…..Cn> and random velocity V=<V1, V2 ,.. Vn >

Step 2: Determine Euclidian distance from all clusters to all instances of Dataset.

Step 3: Determine fitness of all instances (Fi) of clusters.

Step 4: Choose instance having highest fitness in each cluster is chosen as gbest of that cluster. Generate n number of gbest.

Step 5: Compute new velocity, lbest, gbest.

Step 6: Update position of all cluster centers with new velocity Vnew and generate Cnew.

Step 7: if Euclidian distance <= S then repeat from step 3 otherwise display result with final clusters.

IV. EXPERIMENTS AND RESULTS

This section presents the experimental clustering results using FCM, Fuzzy ACO and Fuzzy PSO on Web log files of Makhanlal Chaturvedi University. A little change in cluster center vector has significant effect of total fitness of cluster. Fitness comparison of proposed clustering algorithms and a simulation result is demonstrated on Table I and fig. 1 as shown, cluster formation by using FCM algorithm and fig. 2 and fig.3 shows result obtained after FCM ACO and FCM PSO clustering algorithms respectively.

Figure 1 shows formation of clusters on web log data of Makhanlal Chaturvedi University on fields IP address, Session, User, Date, Time and Page. It also indicates outliers with the different colors.

Figure 2 shows formation of cluster with accurate result on the same dataset using FCM ACO algorithm with computed result values more accurately as in Table I.

Figure 3 shows better and accurate results obtained after FCM PSO than FCM and FCM ACO. It shows god clustering on web log data. It shows how the numbers of errors are reduced as mentioned in Table-I in FCM PSO.

V. CONCLUSION

This paper describes comparison in proposed clustering algorithms with respective parameters as Iterations, Computed error; Standard Deviation .A good clustering algorithm produces higher quality clusters. The fuzzy c-mean algorithm is sensitive to initialization. On other hand the two Swarm intelligence techniques (ACO and PSO) with fuzzy solve various function optimization problems. It overcomes the shortcoming of the fuzzy c- means. The experimental results over web log data shows that the proposed methods are efficient.

Tables at a glance

Table 1

Figures at a glance

Figure 1 Figure 2 Figure 3 Figure 4

References

1. K. Suresh ,R .Madana Mohana, A. Rama Mohan Reddy, A. Subrmanayam, ”Improved FCM algorithm for Clustering on Web usage Mining” ,IEEE 2011.
2. Bighnaraj Naik, Sarita Mahapatra, “Cooperative Swarm Intelligence based Evolutionary Approach to find Optimal Cluster Center in Cluster Analysis”, Journal of Theoretical and Applied information Technology, 15 Aug 2012, Vol. 42, No. 1.
3. Parag M. Kanade ,Lawrence O. Hall, “ Fuzzy Ant Clustering by Centroids Positioning “
4. Zahid Ansari, A. VinayaBabuy, Waseem Ahmed and Mohammad Fazle Azeem, “A Fuzzy Set Theoretic Approach to Discover User Sessions from Web Navigational Data”, IEEE, 2011.