Software development involves number of interrelated factors which has its effect on development and productivity of the software project. Software effort estimation is one of the important activities of software development. The precision and reliability of the effort estimation is very important for software industry because both overestimates and underestimates of the software effort are harmful to software companies. Main objective of this paper is to reduce the relative error rate and to improve the accuracy of the effort estimation by using the software effort estimation models. To estimate the effort for the software project, both algorithmic and Non-algorithmic models has been used. Results from the comparison of algorithmic COCOMO and non algorithmic Trapezoidal membership functions of fuzzy logic have been analysed.
Keywords |
| Software Effort Estimation, Software Effort Estimation models, Fuzzy logic membership functions |
INTRODUCTION |
| Accurate estimation of software development effort in reality has major implications for the management of
software development. As a result, many software effort models [2] for estimating software development effort have
been proposed and are in use. There are several techniques in software effort estimation. Each software project uses its
required effort estimation model. Depending upon the inputs and the specification needed software model is chosen. |
| • Algorithmic Model |
| • Expert Judgment Method |
| • Estimation by Analogy |
| • Non Algorithmic Model |
EFFORT ESTIMATION USING COCOMO MODEL |
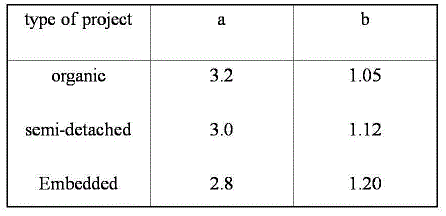
| In the COCOMO model effort estimation[1] input has been given in the form of size. The size is in the form of
Lines of code in direct approach and Function point in indirect approach. The effort required has been calculated for the
two kinds of size using the COCOMO model which is the Algorithmic approach. In the similar way Non-Algorithmic
approach has been applied to the Function point. Using fuzzy logic membership functions such as and Trapezoidal
methods effort is calculated. Then the obtained result has been analysed from these techniques based on relative error.
Software project managers are responsible for controlling project budgets so, they must be able to make estimates of
how much a software development is going to cost. The principal components of project costs are: |
| • Hardware costs. |
| • Travel and training costs. |
| • Effort costs (the costs of paying software engineers).
The dominant cost is the effort cost. This effort can be calculated by using |
| • SLOC |
| • Function point |
| COCOMO estimates are more objective and repeatable than estimates made by methods relying on proprietary
models. The most fundamental calculation in the COCOMO model is the use of the Effort Equation to estimate the
number of Person-Months required to develop a project. COCOMO has cost drivers that assess the project,
development environment, and team to set each cost driver. The cost drivers are multiplicative factors that determine
the effort required to complete your software project. Effort is calculated by, |
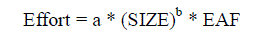 |
| Where 'a' and 'b' are empirically determined constants. Size is calculated as function point |
| The Effort Adjustment Factor in the effort equation is simply the product of the effort multipliers
corresponding to each of the cost drivers. The COCOMO schedule equation predicts the number of months required to
complete your software project[4]. The duration of a project is based on the effort predicted by the effort equation: |
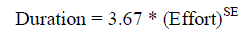 |
| Where Effort is the effort from the COCOMO II effort equation SE Is the schedule equation exponent derived from the
cost Drivers. |
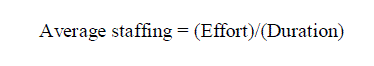 |
| 2.1 Function point calculation: |
| In the model caliberation, initially loc has been given as the input to calculate the effort[3]. Then the function
point has been converted into loc and that has been used in the calculation. In the function point calculation initial
function point has been calculated with the help of data functions and transactional functions. The initial function point
is the unadjusted function point. |
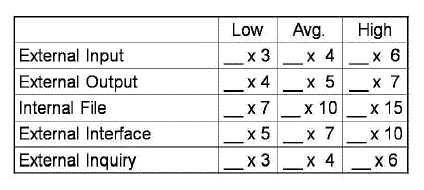
| The data functions are: |
| • Internal Logical File(ILF) |
| • External Interface File (EIF) |
| The transactional functions are: |
| • External Input(EI) |
| • External Output(EO) |
| • External Inquiry(EI) |
| Each function is classified according to its relative functional complexity as low, average or high. The data
functions relative functional complexity is based on the number of data element types (DETs) and the number of record element types (RETs). The transactional functions are classified according to the number of file types referenced
(FTRs) and the number of DETs. The number of FTRs is the sum of the number of ILFs and the number of EIFs
updated or queried during an elementary process. The actual calculation process consists of three steps: |
| • Determination of unadjusted function points(UFP) |
| • Calculation of value of adjustment factor(VAF) |
| • Calculation of final adjusted functional points. |
| Function points can be converted to Effort in Person Hours[5]. Numbers of studies have attempted to relate LOC
and FP metrics. The average number of source code statements per function point has been derived from historical data
for numerous programming languages. Languages have been classified into different levels according to the
relationship between LOC and FP. Programming language levels and Average numbers of source code statements per
function point are given by Complexity matrix. The unadjusted Functional points are evaluated in the following
manner: |
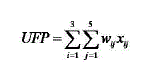 |
| After the calculation of initial fp then the value adjustment factor (VAF) has to be calculated. The VAF
calculation is based on the complexities and rating of factor(r). |
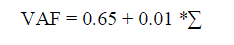 |
| The final fp is calculated using the Unadjusted fp and the VAF which gives the adjusted function point. It is
calculated as |
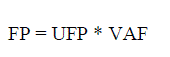 |
| This FP has been converted into corresponding LOC by observing the number of FP per LOC. Then the converted
SIZE has been given as the input to calculation of effort in COCOMO model. |
FUZZY LOGIC |
| Fuzzy logic is a methodology, to solve problems which are too complex to be understood quantitatively,
based on fuzzy set theory. Use of fuzzy sets in logical expression is known as fuzzy logic. A fuzzy set is characterized
by a membership function, which associates with each point in the fuzzy set a real number in the interval [1], called
degree or grade of membership[6]. |
MEMBERSHIP FUNCTIONS OF FUZZY LOGIC |
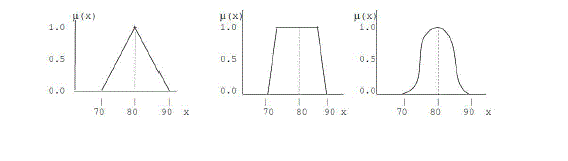
| Triangular, trapezoidal, parabolic etc. are the membership functions. Fuzzy numbers are special convex and
normal fuzzy sets[9], usually with single modal value, representing uncertain quantitative information. Each numerical
value of the domain is assigned a specific value and 0 represents the smallest possible value of the membership
function, while the largest possible value is 1.In many respects fuzzy numbers depict the physical world more
realistically than single valued numbers. Suppose that we are driving along a highway where the speed limit is
80km/hr, we try to hold the speed at exactly 80km/hr, but our car lacks cruise control, so the speed varies from moment
to moment. If we note the instantaneous speed over a period of several minutes and then plot the result in rectangular
coordinates, we may get a curve that looks like one of the curves shown below. |
MODULES OF TRAPEZOIDAL MEMBERSHIP FUNCTION |
| Software Effort Estimation is calculated based on the modules of fuzzy logic membership functions. Membership
functions are modularised as follows: |
| • Fuzzification |
| • Defuzzification |
| • Optimization |
FUZZIFICATION |
| TPMF gives more continuous transition from one interval to another. μA (x) = Trapezoidal (x, a, b, c,
d).Defined by its lower limit a, its upper limit d, and the lower and upper limits of its nucleus or Kernel b and c
respectively: |
DEFUZZIFICATION |
| The fuzzy results generated cannot be used as such hence it is necessary to convert the fuzzy quantities into
crisp quantities for further processing. This can be achieved by using defuzzification process. Defuzzification is the
process of producing a quantifiable result in fuzzy logic, given fuzzy sets and corresponding membership degrees. It
will have a number of rules that transform a number of variables into a fuzzy result, that is, the result is described in
terms of membership in fuzzy sets. The defuzzification is applied to the value that had been obtained from the
fuzzification process[7]. The fuzzified output has to be defuzzified into the real number so that it will give the effort
that has been needed for the effort estimation. |
OPTIMIZATION |
| There are 4 important criterions for assessment of software cost estimation models: |
| 1. VAF (Variance Accounted For): |
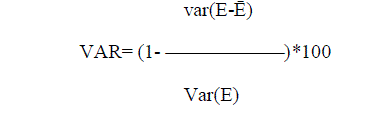 |
| 2. Mean absolute Relative Error : |
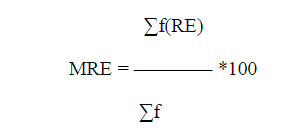 |
| 3. Variance Absolute Relative Error : |
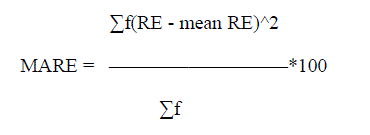 |
| 4. Variance Absolute Relative Error : |
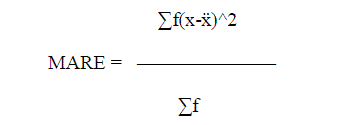 |
| Where x = mean x ,E = actual effort, E = estimated effort, f = frequency |
| The validation results of the experiments are to be assessed by Mean Absolute Relative Error (MARE) for estimation
accuracy. MARE is defined as: for n projects. PRED(N) is the third criteria used for comparison and this reports the
average percentage of estimates that were within N percent of the actual values. Prediction at level n ((Pred (n))is
defined as the percent of projects that have absolute relative error under n. A model which gives lower Mean absolute
Relative Error and higher pred (n) is better than that which gives higher Mean absolute Relative Error and lower
pred(n).A model which gives higher VAF is better than that which gives lower VAF. A model which gives higher pred
(n) is better than that which gives lower pred(n). A model which gives lower Variance Absolute Relative Error is better
than that which gives higher Variance Absolute Relative Error. |
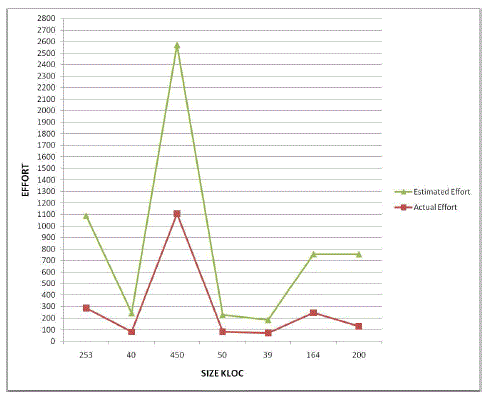
COMPARISON OF EFFORT ESTIMATIONS |
RESULTS AND COMPARISON OF EFFORT ESTIMATION |
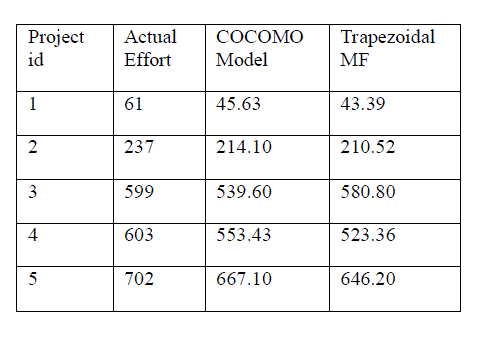 |
CONCLUSION AND FUTURE WORK |
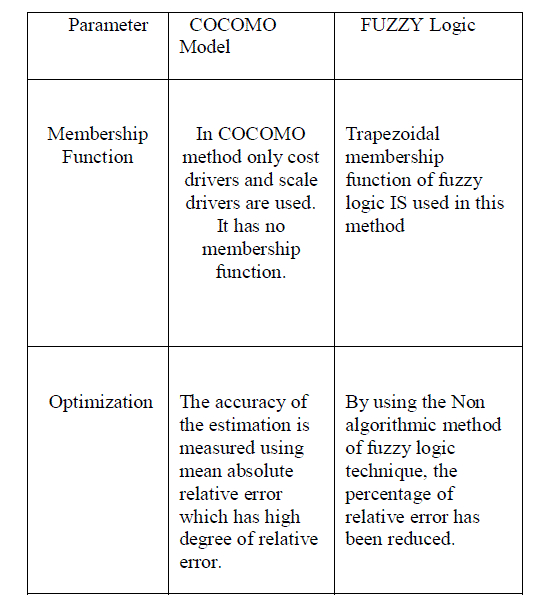 |
| This paper has presented software effort estimation using Fuzzy Logic. By using the Non algorithmic method,
the percentage of relative error has been reduced. It is observed that no method or model of estimation should be
preferred over all others. The key consists in using a variety of methods and tools in combination, new paradigms offer
new implementations over different software projects. By using this extended approach with the standard COCOMO
model and fuzzy membership function we can take advantage of the features of neural network, such as learning ability
and good interpretability. This study can be extended by integrating with neural networks like neuro-fuzzy approach. |
Figures at a glance |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
 |
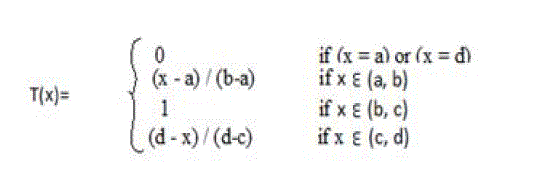 |
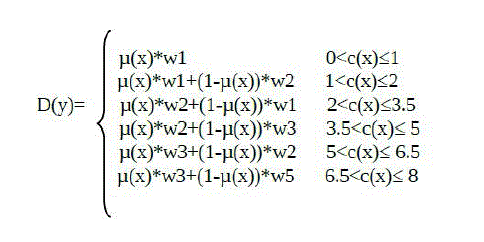 |
| Figure 4 |
Figure 5 |
Figure 6 |
|
References |
- O. Benediktsson, D. Dalcher, K. Reed, and M. Woodman, "COCOMO based effort estimation for iterative and incremental software development", Software Quality Journalvol. 11, pp. 265-281, 2003.
- T. Menzies, D. Port, Z. Chen, J. Hihn, and S. Stukes, "Validation Methods for calibrating software effort models", ICSE '05:Proceedings of the 27th international conference on Software engineering, p.587-595, ACM Press, 2005
- Alaa f. sheta," Estimation of the COCOMO Model Parameters Using Genetic Algorithm for NASA Software Projects", Journal of Computer Science ,vol.7,2(2):118-123,2006
- Ali Idri, alainAbran and LailaKijri, "COCOMO cost modeling using Fuzzy Logic", International conference on Fuzzy Theory and technology, Atlantic, 7New Jersy, March 2000
- IFPUG. Function Point Counting Practices Manual: Release 4.0. International Function Point Users Group, Princeton Junction, NJ, 1994.
- .A. ZADEH, "Fuzzy Sets, Information and Control", Communication of the ACM ,pp.8, 338-353, 1965.
- Roger S. Pressman, Software Engineering; A practitioner Approach, Mc Graw-Hill International Edition, Sixth Edition, 2005
- Baiely,j.wBasili,"A Meta model for Software Development ResourceExpenditure", Proc. Intl. Conference Software Egg.,pp : 107-115,1981
- Musilek, P., Pedrycz, W., Succi, G., Reformat, M., "Software Cost Estimation with Fuzzy Models". ACM SIGAPP Applied Computing Review, pp.8(2), 24-29, 2000.
- L.A. ZADEH., ., "From Computing with numbers to computing with words-from manipulation of measurements to manipulation of perceptions", Int. J. Appl. Math. Computer Sci., , Vol.12, No.3, 307-324., 2002.
|