A Flux Formula For Weighted Manifolds

Abstract

In this article, we derive a flux formula in a weighted manifold, using the weighted Newton transformations and introducing the notion of weighted higher order mean curvature, this formula generalizes. Reilly’s original formula and the flux formula obtained by Alias, Lopez and Malcarne [1]. In particular, we obtain a similar balancing formula obtained by Rosenberg. Finally, we give some special cases of our formula.

Keywords

Weighted manifolds, Weighted, Newton transformation, rth mean curvature, Weighted mean curvature

Introduction

Most of the useful integral formulas in Riemannian geometry are obtain by computing the divergence of certain vector fields and then apply the divergence theorem. In the authors gave a flux formula. In particular, they derive a similar balancing formula given by Rosenberg [2]. As an application to this flux formula they gave an estimation of the higher order mean curvature H_r of a hypersurface in space forms by the geometry of its boundary [1]. Motivated by the work of these authors, we give in this work a flux formula in the case of weighted manifolds. Recall that a weighted manifold (called also a manifold with density) is a Riemannian manifold M endowed with a smooth positive density e^-f with respect to the Riemannian measure. We proof the following proposition.

Proposition 1

Let 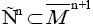an oriented connexion sub-manifold of 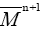and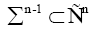 a compact hyper-surface of Pⁿ . 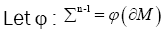a compact oriented hyper-surface of boundary 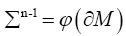Denoting by N the global vector fields normal to Mⁿ, and ν the outpointing vector normal to 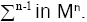Then for 1 ≤ k ≤ n and for every conformal vector field 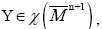we have

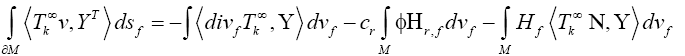
Where 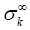is the weighted Newton transformations, and H_r,f is the weighted higher order mean curvature.

As a consequence of this proposition, we obtain some special cases. In particular, we obtain a balancing formula for 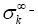minimal hyper-surface in space forms. The paper is organized as follows. Section 2 provides some preliminaries. The main results of the paper are contained in Section 3. Throughout the paper everything (manifolds, metrics, etc.) is assumed to be C^∞ -differentiable and oriented [3-5].

Preliminaries

In this section we introduce the basic notations used in the paper. we will recall some definitions and properties of the weighted symmetric functions and the weighted Newton transformations. For more details see [3],[7].

Let be a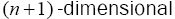 Riemannian manifold. Let 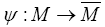be an isometrically immersed hypersurface. Denoting by 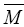and 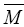the Levi civita connections of 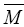and 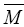respectively. Then, the Weingarten formulae of the hypersurface is written as

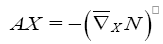
Where ^Τ is the shape operator of the hypersurface M with respect to the Guass map N, and ^Τ denotes the orthogonal projection on the vector bundle tangent to M,

It is well know that A is a linear self adjoint operator. At each point p∈M, its eigenvalues μ₁,..., μ_n are the principales curvatures of M [6,7].

Associate to the shape operator A , define the weighted elementary symmetric fucntions 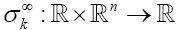recursively by:

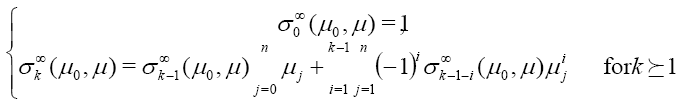
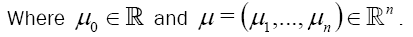
In particular 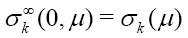is nothing but the classical elementary symmetric functions define in [8].

Definition

The weighted Newton transformations (W.N.T) 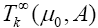are define inductively form A by

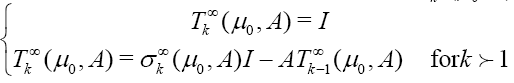
Where 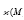denote the identity of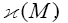

Or equivalentely by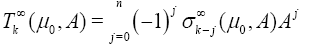

Where 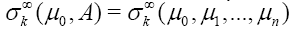and n μ ,...,μ 1 are the eigenvalues of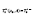

We denote to simplify 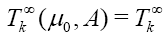and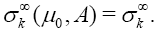

In particular 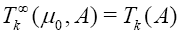is the classical Newton transformations introduced in [8]

These two quantities has the same proprietes of the classical symmetric functions and Newton transformations [3].

Proposition 2

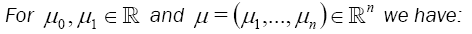
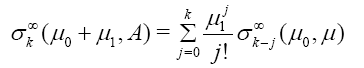
In particular 1,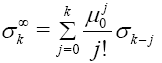

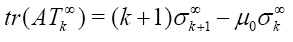
And the 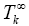eigenvalue of 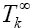is equal to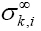

Where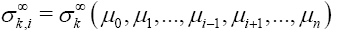

Definition 1: The weighted r^th mean curvature H_r,f is given by:

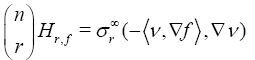
Where ν is the outpointing vectors field normal to M in

In particular for r =1, we have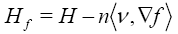

Is the weighted mean curvature of the hypersurface M

Definition 2: We say that an hypersurface M of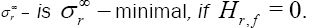

In particular; M is f −minimal, if H_f= 0 . Or equivalentely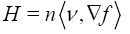

Definition 3: The weighted divergence of the weighted Newton transformations is define by:

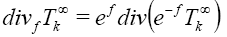
Where

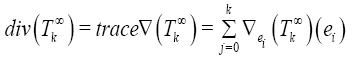
And {e₁,…,e_n} is an orthonormale basis of the tangent space of M.

In particular, if f vanish identiqualy and μ=0, then we obtain the classical difinition of the divergence of the Newton tranformations.

I found here some isoperimetrics inequalities. Now I am trying to find a variational formula for the wighted higher order mean curvature [9].

Conclusion

In conclusion, my steps are:

1. Calculate the divergence 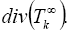(The fact that we calculate this quantity is to use it in the two last steps by using the divergence theorem for the weighte Newton transformation).

2. Compare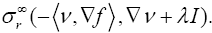

3. Find variation (critical point) for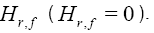

4. Minimise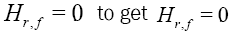

Forn the two first points, I found the way.

I think the two last ones are equivalent to the study of the variation

If you have an idea about how we study the two last points, because if we can find such

realtion, this result gives a geometric interpretation of our quantity ( H _r,f ).

References

1. Alías LJ, et al. Constant higher-order mean curvature hypersurfaces in Riemannian spaces. J the Instof MathJussieu.2006; 5: 527-562.
2. BarbosaJL and EarpRS. Prescribed mean curvature hypersurfaces in Hn+1(-1) with convex planar boundary I. GeometriaeDedicata. 1998; 71: 61-74.
3. CaseJS. A notion of the weighted for manifolds with sk-curvature density.AR-XIV. 2016; 2: 1409-4455.
4. CastroK and RosalesK. Free boundary stable hyper-surfaces in manifolds with density and rigidity results. AR-XIV: 1: 1311-1952.
5. EspinarJM. Manifolds with density, applications and gradient Schrodinger operators.AR-XIV. 6: 1209.6162.
6. KoisoM. Symmetry of hypersurfaces of constant mean curvature with symmetric boundary. Math Z. 1986; 191; 567-574.
7. MorganF. Manifolds with density. NoticesAmer Math Soc.2005; 52:853-858.
8. ReillyRC.Variational properties of functions of the mean curvature for hyper-surfaces in space forms. J Differential Geom 1973; 8: 465-477.
9. RosenbergH. Hypersurfaces of constant curvature in space forms. BullSc Math.1993; 117: 211-239.