Keywords
|
| Association rule mining, Data mining, Support, Confidence, Frequent Itemsets, Algorithms |
INTRODUCTION
|
| The size of the database has been increasing in a rapid manner in the modern years. This leads to the development of tools which is capable in the automatic extraction of knowledge from the data. The term data mining deals with the automatic discovery of hidden information within the databases. In the major areas of datamining ,the discovery of frequent items is a difficult task. It was formulated by Agrawal et al in the year 1993 and is known as market basket problem. In this problem, a large collection of transactions is given with large set of items. The task is to find association between the various items within these baskets. The discovery of association rule is dependent on the discovery of frequent sets. Frequent item plays a major role in data mining task. Association rules describe how often items are purchased together. For example , a rule “bread => Jam” 80% states that eight out of ten customers who bought bread also bought jam. These such rules are useful for decision making in various areas. These areas includes product pricings, inventory management, sales promotion strategies etc. Here, we explain the concept of frequent item sets , association rule mining problems and an algorithm to find the frequent items. |
PROBLEM DEFINITION
|
| Let A = {A1, A 2,..., Am} be a set of itemset. Let D be a set of database transactions where each transaction T is a nonempty itemset such that T ⊆ A. Each transaction is connected with an identifier, called a TID. Let X be a set of items. A transaction T is said to contain in X if X ⊆ T. An association rule is an implication of the form X⇒ Y, where X⊂ I, Y ⊂ I, X ≠∅, Y≠ ∅, and X ∩Y = φ. The rule X ⇒ Y holds in the transaction set D with support s.Here s denotes the percentage of transactions in D that contain X ∪Y (i.e., the union of sets X and Y say, or, both X and Y). This is taken to be the probability, P(X ∪Y). The rule X ⇒ Y has confidence c in the transaction set D.Here c denotes the percentage of transactions in D containing X that also contain Y. This is taken as the conditional probability, P(Y|X). support(X⇒Y) =P(X ∪Y) confidence(X⇒Y) =P(Y|X). |
PROBLEM DECOMPOSITION
|
| The problem of deriving association rules can be decomposed in to two sub divisions: |
| 1. Find all sets of items (item sets) whose support is greater than the user-mentioned minimum support. Such item sets are called frequent item sets[1]. |
| 2. Use the obtained frequent item sets to generate the possible rules. |
| Downward Closure Property: A set which is a subset of frequent set is also a frequent set. |
| Upward Closure Property: A set which is a superset of infrequent set is also a infrequent set. |
| Maximal Frequent set: A frequent set is a maximal frequent set if it is a frequent set and no superset of this is a frequent set. |
| Border set: An item set is a border set if it is not a frequent set, but all its proper subsets are frequent sets[1]. |
LITERATURE REVIEW
|
| C.K.S. Leung and Q.I. Khan In this paper with advances in technology, a flood of data can be produced in many applications such as sensor networks and Web click streams. This calls for efficient techniques for extracting useful information from streams of data. In this paper, we propose a novel tree structure, called DSTree (Data Stream Tree), that captures important data from the streams. By exploiting its nice properties, the DSTree can be easily maintained and mined for frequent itemsets as well as various other patterns like constrained itemsets. |
| S.K. Tanbeer, C.F. Ahmed in this paper finding frequent patterns in a continuous stream of transactions is critical for many applications such as retail market data analysis, network monitoring, web usage mining, and stock market prediction. Even though numerous frequent pattern mining algorithms have been developed over the past decade, new solutions for handling stream data are still required due to the continuous, unbounded, and ordered sequence of data elements generated at a rapid rate in a data stream. Therefore, extracting frequent patterns from more recent data can enhance the analysis of stream data. In this paper, we propose an efficient technique to discover the complete set of recent frequent patterns from a high-speed data stream over a sliding window. We develop a Compact Pattern Stream tree (CPS-tree) to capture the recent stream data content and efficiently remove the obsolete, old stream data content. We also introduce the concept of dynamic tree restructuring in our CPS-tree to produce a highly compact frequency-descending tree structure at runtime. The complete set of recent frequent patterns is obtained from the CPS-tree of the current window using an FP-growth mining technique. Extensive experimental analyses show that our CPS-tree is highly efficient in terms of memory and time complexity when finding recent frequent patterns from a high-speed data stream. |
| C. Giannella, J. Han, J. Pei Although frequent-pattern mining has been widely studied and used, it is challenging to extend it to data streams. Compared to mining from a static transaction data set, the streaming case has far more information to track and far greater complexity to manage. Infrequent items can become frequent later on and hence cannot be ignored. The storage structure needs to be dynamically adjusted to reflect the evolution of itemset frequencies over time. |
| P.S.M. Tsai Association rule mining is an important research topic in the data mining community. There are two difficulties occurring in mining association rules. First, the user must specify a minimum support for mining. Typically it may require tuning the value of the minimum support many times before a set of useful association rules could be obtained. However, it is not easy for the user to find an appropriate minimum support. Secondly, there are usually a lot of frequent itemsets generated in the mining result. It will result in the generation of a large number of association rules, giving rise to difficulties of applications. In this paper, we consider mining top-k frequent closed itemsets from data streams using a sliding window technique. A single pass algorithm, called FCI_max, is developed for the generation of top-k frequent closed itemsets of length no more than max_l. Our method can efficiently resolve the mentioned two difficulties in association rule mining, which promotes the usability of the mining result in practice. |
ITEMSET MINING
|
| A. Frequent Itemset Mining |
| Frequent itemsets are the items that appears repeatedly in the transactions. The main goal of frequent itemset mining is to identify all the itemsets in the transaction data set, which are frequently purchased. The Apriori algorithm is the initial solution for the frequent pattern mining problem.To overcomes the problems of Aprori, which generates more candidate sets and require more scans of database FP-Growth has been proposed. Uses FP-Tree data structure without any candidate generation and using only two database scans. In the framework of frequent itemsets mining the importance of an item are not considered. |
| B. Weighted Frequent Itemset Mining |
| In this, the importance of the items is represented in the form of weights.The weight of a pattern p is the ratio of the sum of all its weight to the length of p. The relative importance of an item is not measured in the case of frequent itemset mining. The weighted association rule mining is introduced to address this problem. Here weights are given to items to represent the importance of an item to the users. Where this weight indicates the importance of itemset. |
| C. High Utility Itemset Mining |
| In the data mining field Utility mining is an essential one for finding the items with high profits. Utility Mining focuses the frequency of the itemsets as well as the utility associated with the itemsets. In High Utility Itemset Mining the purpose is to identify itemsets that have utility values beyond the given utility threshold. Utility of an itemset is defined as the cross product of its external utility and its internal utility. |
NEED FOR THE STUDY
|
| Nowadays,large amount of data is produced in all fields. The produced data are in the form of data streams .These streaming data is continous and not in bounded manner .The streaming data is also not uniformly distributed. It is difficult to find frequent items from the data streams because streaming data has to be scanned multiple times . Once the streams flow through, we lose them. Hence, we need some techniques to process and capture the important contents of the streams and ensure that the captured data can fit into memory. Moreover, as data distributions in the streams are usually changing with time, a currently infrequent itemset may become frequent in the future and vice versa. So,pruning of the infrequent items at the early stage should be avoided. Or else, the complete information such as frequencies of some itemsets (as it is impossible to recall those pruned itemsets) cannot be obtained. Numerous algorithms have been proposed to mine FIs from streams.So we propose a new algorithm to find frequent items using damped window model which is not fixed size window.It give importance to previous batch data and also current data. |
ALGORITHM
|
| Here, we propose array based tail node based algorithm for mining frequent itemsets using damped window model. The proposed algorithm UDS-FIM mainly consists of three procedures: (1) Damped window initialization (2) creating a global UDS-Tree; (3) mining frequent itemsets from the global UDS-Tree; |
| A. DAMPED WINDOW INITIALIZATION |
| The damped window initialization phase is initiated while the number of transactions generated so far in a transaction data stream is less than or equal to a user-predefined window size w (batch). In this phase, each item of the new incoming transaction is transformed into its global UP table. |
| In general, after w batches of streaming data arrive, the proposed algorithm would traverse all O (N) nodes w−1 times and updated O(w2N) older expected support values (i.e., O(w2N) multiplications). After w=3 batches of streaming |
| data arrived, the damped algorithm traversed N=9 nodes twice and updated 27 older expected support values (involving 27 multiplications: 9 after B2 arrived and 18 after B3 arrived). To reduce the update cost, we propose an improved algorithm. Instead of updating older expected support values and appending the new values, our improved algorithm just appends the new expected support values to the list. Then, when computing the expected support of X in the data stream (of w batches so far, i.e., B1:w ≡ B1 Bw), the improved algorithm uses the following equation instead: |
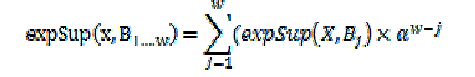 |
| where (X,Bj) is the expected support of X stored in the j-th position of the list (representing Bj of streaming data) and α ∈ (0, 1] is the fading factor. By doing so, we avoid O(w2N) multiplications during the update process. The computation of expected support using Equation (2) involves only O(wN) multiplications on O(N) FIs. |
| B. PARAMETERS OF UDS TREE |
| Let itemset X = {x1, x2, x3… xu} be a sorted itemset, and the item xu is called Array tail-item of X. When the itemset X is added into a tree T in accordance with its order, the node on the tree that represents this array tail-item is called as a array tail-node; a node that has no children is called as a leaf node; a node that is neither a array tail-node nor a leafnode is called as a normal node. |
| Before a transaction itemset is added into a UDS-Tree, its corresponding probability values are appended to the table. |
| C. ALGORITHM |
| Input: A Damped Tail Node Tree T, a global itemsets header table H, and a minimum expected support number minExpSN. |
| Output: FIs (frequent itemsets) |
| (1) First computing the expected support of X in the data stream (of w batches), |
| (2) Add the batch information on info field on each leaf-node to the field addInfo; |
| (3) For each item x in H (from the last item) do |
| (4) If(x.esnT≥minthreshold ) //x.esnT is from the header table H |
| (5) Generate an itemset X = x ; |
| (6) Copy X into FIs; |
| (7) Create a sub header table Hx for X; |
| (8) If(Hx is not empty) |
| (9) Create a prefix UDS-Tree Tx for X; |
| (10) Call SubMining(Tx, Hx, X) |
| (11) Pruning non frequent itemsets |
| (12) End if |
| (13) End if |
| (14) Pass the information of addInfo field to parent nodes; |
| (15) End for |
| (16) Return FIs. |
| SubProcedure SubMining (Tx, Hx, X) |
| (17) For each item y in Hx (from the last item) do |
| (18) Generate an itemset Y= X∪ ; |
| (19) Copy Y into FIs; |
| (20) Create a header table Hy for Y; |
| (21) If (Hy is not empty) |
| (22) Create a prefix UDS-Tree Ty for Y; |
| (23) Call SubMining(Ty, Hy, Y) |
| (24) End if |
| (25) Pass the information of info list field to parent nodes; |
| (26) End for |
CONCLUSION
|
| In this paper, we proposed tail node tree-based mining algorithms that use a damped window model to mine dynamic streams of uncertain data for frequent itemsets. The UDS-FIM maintains the frequent items in the UDS tree with preminsup to find frequent itemsets.The mined items are then stored in the stream structure with the expected support values.When the next batch arrives,it updates the UDS-stream structure. The improved algorithm reduces the costs by just appending the expected support values of recent data.The UDS FIM keeps only one support value for each itemset.The UDS FIM requires shortest less amount amount of time to find frequent itemsets when compared with other algorithms.. |
Figures at a glance
|
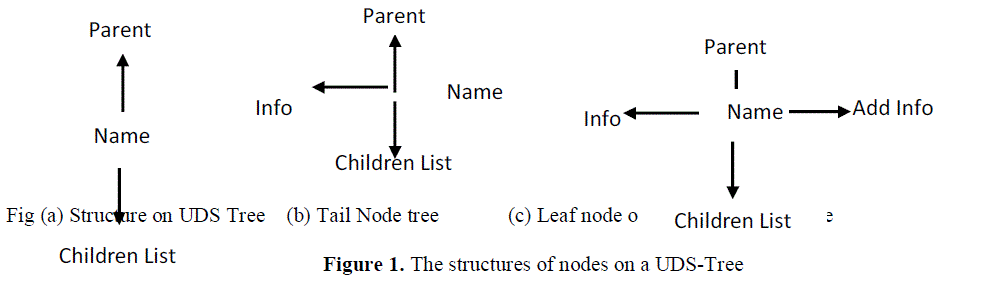 |
| Figure 1 |
|
References
|
- K.Jothimani and Dr.AntonySelvadossThanamami,”EDS-FI:Efficient Data Structure for Mining Frequent Itemsets”,under InformationandCommunication Technology including computer Science(ICT)from ISCA(Indian Science Congress Association),Kolkatta 3rd -7th January,2013.
- K.Jothimani and Dr.AntonySelvadossThanamami ,”Determining the factors for mining Frequent Itemsets in Data SDtreams”,NCCICT held at VELTECH Dr.RR& SR Technical University,Avadi during 12th -13th August,2011,pp-127-130,ISBN 978-93-80624-43-3.
- C.W. Lin and T.P. Hong, "A new mining approach for uncertain databases using CUFP trees," Expert Systems with Applications, Vol.39, no.4,pp.4084-4093, 2011.
- G. Liao, L. Wu, C. Wan, and N. Xiong, A practice probability frequent pattern mining method over transactional uncertain data streams, in 8thInternational Conference on Ubiquitous Intelligence and Computing. 2011, pp.563-575.
- C.C. Aggarwal and P.S. Yu, "A survey of uncertain data algorithms and applications," IEEE Transactions on Knowledge and Data Engineering,Vol.21, no.5, pp.609-623, 2009.
- C.K. Leung, M.A.F. Mateo and D.A. Brajczuk, A tree-based approach for frequent pattern mining from uncertain data, in 12th Pacific-AsiaConference on Knowledge Discovery and Data Mining (PAKDD 2008). 2008, pp.653-661.
- K.Jothimani and Dr.AntonySelvadossThanamami,” CB Based Approach for Mining Frequent Itemsets”, International Journal of Modern EngineeringResearch (IJMER), ISSN: 2249-6645, Vol.2, Issue.4, July-Aug. 2012 pp-2508-2511.
- X. Sun, L. Lim and S. Wang, "An approximation algorithm of mining frequent itemsets from uncertain dataset," International Journal ofAdvancements in Computing Technology, Vol.4, no.3, pp.42-49, 2012.
- T. Calders, C. Garboni and B. Goethals, Approximation of frequentness probability of itemsets in uncertain data, in IEEE International Conference onData Mining (ICDM 2010). 2010, pp.749-754.
- L. Wang, D.W. Cheung, R. Cheng, S. Lee, and X. Yang, "Efficient Mining of Frequent Itemsets on Large Uncertain Databases," IEEE Transactionson Knowledge and Data Engineering, no.99(PrePrints), 2011.
- C.K. Leung, C.L. Carmichael and B. Hao, Efficient mining of frequent patterns from uncertain data, in International Conference on Data MiningWorkshops (ICDM Workshops 2007). 2007, pp.489-494
- .Q. Zhang, F. Li and K. Yi, Finding frequent items in probabilistic data, in International Conference on Management of Data (ACM SIGMOD). 2008,pp.819-831.
- C.K. Leung and F. Jiang, Frequent itemset mining of uncertain data streams using the damped window model, in 26th Annual ACM Symposium onApplied Computing (SAC 2011). 2011, pp.950-955.
- C.K. Leung and F. Jiang, Frequent pattern mining from time-fading streams of uncertain data, in 13th International Conference on Data Warehousingand Knowledge Discovery (DaWaK 2011). 2011, pp.252-264.
- K.Jothimani and Dr.AntonySelvadossThanamami,” An Efficient Approach for Mining Frequent Itemsets with Large Windows”, InternationalJournal Of Computational Engineering Research, ISSN: 2250–3005, Vol.2, Issue No.3,May-June,2012,pp.923-92
|