A New Infinite Series with Proof of Convergence and Irrational Sum

Abstract

This is a sum of reciprocal squares all the way to infinity that is dealt with in a new alternating fashion of adding and subtracting consecutive terms in the ratio 2:1 respectively.

Keywords

Convergence, Irrational, Reciprocal squares, Infinity.

Introduction

Definition: The series was first stated by the author on the Math forum [1] as “For n=1 to infinity, starting with 1 the next two consecutive terms of 1/n^2 are added, then the next term of 1/n^2 is subtracted, the following two consecutive terms of 1/n^2 are added, the subsequent term of 1/n^2 is subtracted etc... repeating like that all the way to infinity.” The first 10 terms of the series are thus:

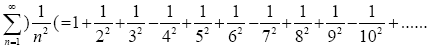(1)

Where the use of the inverted brackets) (denotes “Add together two consecutive terms of this series then minus the next term and repeat this in an alternating fashion”.

The infinite sum of all terms in series (1) became known as the Basel problem and was first solved by Leonhard Euler [2] in the seventeen hundreds. This has been famously proved to converge exactly to π²/6. By algebraic manipulation, the sum of the new alternating series in (1) can be rewritten as a difference of the original sum of reciprocal squares and the new sum expressed as an exact result:-

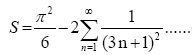(2)

Proof of Convergence

By calculating the first 40 consecutive terms and plotting their cumulative sums on a graph it is clear that the series is convergent and that the limit exists (Figure 1).

Figure 1: Series is convergent

We note an apparently fast rate of convergence and that the sum appears to be tending to a limiting value of around ≈1.4. Convergence can also be proved analytically by using an appropriate test. The comparison test in particular is used in this paper as follows. The first term in (2) is a constant, so all we need to prove is that the sum in the second term converges. This can be compared with the similar p-series for the special case of p=2 (Riemann Zeta 2).

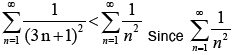
Since converges absolutely, so the new series invented in this paper also converges absolutely.

Proof of Irrational Sum

Inputting the series into Wolfram Alpha [3] the sum value at infinity is computed to be approximately 1.4014680389755... This limiting value was found by calculating up to 10 million terms. This in fact is an irrational number that can be proved to be irrational by a comparison test to sums of other very similar series.

From (2) if we let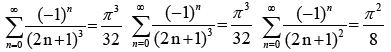

The following series have been proved to have irrational sums expressed in terms of π:

Conclusion

Because x is intrinsically of a similar construct to the above series and their sums converge to irrational numbers, it follows that the overall sum of the new series in (2) is equally irrational.

References

1. Ahad A.Proofs of my new infinite alternating series. Google Groups. sci.math.2017.
2. Eremenko A.How Euler found the sum of reciprocal squares.2013.
3. https://www.wolframalpha.com/examples/Math.