Keywords
|
| Ensemble-methods, Classification, Data stream, Random Forest, Rotation Forest, Decision Trees, Principal component analysis |
INTRODUCTION
|
| Combining classifiers is a very popular research area known under different names in the literature such as committees of learners, mixture of experts, classifier ensembles, multiple classifier systems, and consensus theory [1]. The basic idea is to use more than one classifier, hoping that the overall accuracy will be better. Ensemble performances depend on two main properties: the individual accuracy and diversity [14]. |
| Principal component analysis (PCA) is a technique that is useful for the compression and classification of data. The purpose is to reduce the dimensionality of a data set (sample) by finding a new set of variables, smaller than the original set of variables, that nonetheless retains most of the sample's information. By information we mean the variation present in the sample, given by the correlations between the original variables [2] [15]. The new variables, called principal components (PCs), are uncorrelated, and are ordered by the fraction of the total information each retains. |
| Decision tree is a predictive model that uses a set of binary rules applied to calculate a target value and it can be used for classification (categorical variables) or regression (continuous variables) applications. Rules are developed using software available in many statistics packages. In decision tree different algorithms are used to determine the “best” split at a node. It is easy to interpret the decision rules and it is nonparametric so it is easy to incorporate a range of numeric or categorical data layers and there is no need to select unimodel data and classification is fast once rules are developed [3] [13]. |
| Random Forest (RF) is a classification and regression method based on the aggregation of a large number of decision trees. Specifically, it is an ensemble of trees constructed from a training data set and internally validated to yield a prediction of the response given the predictors for future observations [6]. There are several variants of RF which are characterized by 1) the way each individual tree is constructed, 2) the procedure used to generate the modified data sets on which each individual tree is constructed, 3) the way the predictions of each individual tree are aggregated to produce a unique consensus prediction [4]. |
| Rotation Forest is an ensemble classifier using many decision tree models and it can be used for classification or Regression. It was first proposed by Rodriguez and Alonso [10]. Each base learner is trained with a slightly rotated original training data set. The rotation matrix is calculated differently for each base learner by bootstrapping from the training data and from the classes. This method works with only numeric features. If the data set has other types of features, they are transformed to numeric representation [12]. The results of the base learners are combined using majority voting for all of the methods. Accuracy and variable importance information is provided with the results. A different subset of the training data is selected with replacement, to train each tree and the remaining data are used to estimate error and variable importance [11]. |
| In Extended Space Forest the training sets used in the training of the base learners of an ensemble are generated by adding new features to the original ones. For each base learner, a different extended training set is generated. The extended training sets are generated by adding new features obtained from the original features. So each base learner is trained with a different training set. The extended space method is a general framework that can be used with any ensemble algorithm [8] [5]. For example, if bagging is chosen as ensemble algorithm (ENS), the training data for each base learner (Li) would be obtained from a random sample, with replacement, from Ei data set. If random subspace is chosen as ensemble algorithm, the base learner would be trained with the randomly selected features of Ei data set. |
LITERATURE REVIEW
|
| In this section an empirical review on Decision tree, Principal Component Analysis, Rotation Forest and Random Subspaces are explained. |
| J.J. Rodriguez et al., (2004) described a new method for ensemble generation is presented. It is based on grouping the attributes in different subgroups, and to apply, for each group, an axis rotation, using Principal Component Analysis. If the used method for the induction of the classifiers is not invariant to rotations in the data set, the generated classifier can be very different. Hence, once of the objectives aimed when generating ensembles is achieved, that the different classifiers were rather diverse. The majority of ensemble methods eliminate some information (e.g., instances or attributes) of the data set for obtaining this diversity. The proposed ensemble method transforms the data set in a way such as all the information is preserved. The experimental validation, using decision trees as base classifiers, is favorable to rotation based ensembles when comparing to Bagging, Random Forests and the most well-known version of Boosting. |
| C.-X. Zhang et al., (2009) described a novel ensemble classifier generation method by integrating the ideas of bootstrap aggregation and Principal Component Analysis (PCA). To create each individual member of an ensemble classifier, PCA is applied to every out-of-bag sample and the computed coefficients of all principal components are stored, and then the principal components calculated on the corresponding bootstrap sample are taken as additional elements of the original feature set. A classifier is trained with the bootstrap sample and some features randomly selected from the new feature set. The final ensemble classifier is constructed by majority voting of the trained base classifiers. The results obtained by empirical experiments and statistical tests demonstrate that the proposed method performs better than or as well as several other ensemble methods on some benchmark data sets publicly available from the UCI repository. Furthermore, the diversity-accuracy patterns of the ensemble classifiers are investigated by kappaerror diagrams. |
| T.K. Ho et al., (2008) explained about decision trees that focus on the splitting criteria and optimization of tree sizes. The dilemma between over fitting and achieving maximum accuracy is seldom resolved. A method to construct a decision tree based classifier is proposed that maintains highest accuracy on training data and improves on generalization accuracy as it grows in complexity. The classifier consists of multiple trees constructed systematically by pseudo randomly selecting subsets of components of the feature vector, that is, trees constructed in randomly chosen subspaces. |
| L.I. Kuncheva et al., (2007) described that Rotation Forest is a recently proposed method for building classifier ensembles using independently trained decision trees. It was found to be more accurate than bagging, Ada Boost and Random Forest ensembles across a collection of benchmark data sets. This paper carries out a lesion study on Rotation Forest in order to find out which of the parameters and the randomization heuristics are responsible for the good performance. Contrary to common intuition, the features extracted through PCA gave the best results compared to those extracted through non-parametric discriminate analysis (NDA) or random projections. The only ensemble method whose accuracy was statistically indistinguishable from that of Rotation Forest was LogitBoost although it gave slightly inferior results on 20 out of the 32 benchmark data sets. It appeared that the main factor for the success of Rotation Forest is that the transformation matrix employed to calculate the (linear) extracted features is sparse. |
| C.-X. Zhang et al., (2010) explained about Rotation Forest, an effective ensemble classifier generation technique, works by using principal component analysis (PCA) to rotate the original feature axes so that different training sets for learning base classifiers can be formed. This paper presents a variant of Rotation Forest, which can be viewed as a combination of Bagging and Rotation Forest. Bagging is used here to inject more randomness into Rotation Forest in order to increase the diversity among the ensemble membership. The experiments conducted with 33 benchmark classification data sets available from the UCI repository, among which a classification tree is adopted as the base learning algorithm, demonstrate that the proposed method generally produces ensemble classifiers with lower error than Bagging, Ada Boost and Rotation Forest. The bias–variance analysis of error performance shows that the proposed method improves the prediction error of a single classifier by reducing much more variance term than the other considered ensemble procedures. Furthermore, the results computed on the data sets with artificial classification noise indicate that the new method is more robust to noise and kappa-error diagrams are employed to investigate the diversity–accuracy patterns of the ensemble classifiers. |
PROPOSED WORK
|
| A. Ensembles of Classifiers: |
| Ensembles of classifiers mimic the human nature to seek advice from several people before making a decision where the underlying assumption is that combining the opinions will produce a decision that is better than each individual opinion. Several classifiers (ensemble members) are constructed and their outputs are combined usually by voting or an averaged weighting scheme to yield the final classification. In order for this approach to be effective, two criteria must be met: accuracy and diversity. Accuracy requires each individual classifier to be as accurate as possible i.e. individually minimize the generalization error. Diversity requires minimizing the correlation among the generalization errors of the classifiers. Proposed system focuses on ensemble classifiers that use a single induction algorithm, for example the nearest neighbor inducer. This ensemble construction approach achieves its diversity by manipulating the training set. Several training sets are constructed by applying bootstrap sampling (each sample may be drawn more than once) to the original training set. Each training set is used to construct a different classifier where the repetitions fortify different training instances. This method is simple yet effective and has been successfully applied to a variety of problems such as medical dataset and analysis of gene expressions. |
| Fast Rotation Forest is one of the current state-of-the-art ensemble classifiers. This method constructs different versions of the training set by employing the following steps: First, the feature set is divided into disjoint sets on which the original training set is projected. Next, a random sample of classes is eliminated and a bootstrap sample is selected from every projection result. Principal Component Analysis is then used to rotate each obtained subsample. Finally, the principal components are rearranged to form the dataset that is used to train a single ensemble member. The first two steps provide the required diversity of the constructed ensemble. |
| B. Fast Rotation Forests: |
| A classical Rotation Forest induction procedure grows trees independently from one another. Hence, each new tree is arbitrarily added to the forest. One can therefore wonder if all those trees contribute to the performance improvement. By using classical RF induction algorithms, some trees make the ensemble performance decrease, and that a well selected subset of trees can outperform the initial forest [15]. Figure 1 illustrates this statement by showing the evolution of error rates obtained with a sequential tree selection process called SFS (Sequential Forward Search) applied on an existing 300-trees forest built with Breiman's RF. |
| Figure 1 states that selection technique starts with an empty set and iteratively adds a classifier according to a given criterion (e.g. the error rate obtained on a validation dataset). At each iteration of the SFS process, each classifier in the pool of candidate classifiers is evaluated and the one that optimizes the performance of the ensemble is kept. The results presented show that there always exists at least one sub-forest that significantly outperforms the initial one, sometimes with ten times less trees. The performance of the RF could therefore be improved by removing from the ensemble well selected trees. The idea with FRF is to avoid the induction of trees that could make the forest performance decrease, by forcing the algorithm to grow only trees that would suit to the ensemble already grown. |
| In this proposed system that the FRF induction could benefit from adopting a parallel approach, that is to say by making the tree induction dependent of the ensemble under construction. For that purpose, it is necessary to guide the tree induction by bringing to the process some "information" from the sub-forest already built. To do so, the idea behind the Fast Random Forest (FRF) algorithm is to perform a resampling of the training data that is halfway between bagging and boosting : proceed first to a random sampling with replacement of N instances, where N stands for the initial number of training instances (bagging), and then reweight the data (some kind of boosting). The reason for this choice is to keep using the two efficient randomization processes (i.e. bagging and Random Feature Selection) of Breiman's RF, and to improve RF accuracy by using the adaptive resampling principle of boosting. |
| Principal Component Analysis is then used to rotate each obtained subsample. Finally, the principal components are rearranged to form the dataset that is used to train a single ensemble member. The first two steps provide the required diversity of the constructed ensemble. |
| A tree can be "learned" by splitting the source set into subsets based on an attribute value test. This process is repeated on each derived subset in a recursive manner called recursive partitioning. The recursion is completed when the subset at a node has all the same value of the target variable, or when splitting no longer adds value to the Employing dimensionality reduction to a training set has the following advantages: |
| • It reduces noise and de-correlates the data. |
| • It reduces the computational complexity of the classifier construction and consequently the complexity of the classification. |
| • It can alleviate over-fitting by constructing combinations of the variables. These points meet the accuracy and diversity criteria which are required to construct an effective ensemble classifier and thus render dimensionality reduction a technique which is tailored for the construction of ensemble classifiers. |
| Figure 1 states that selection technique starts with an empty set and iteratively adds a classifier according to a given criterion (e.g. the error rate obtained on a validation dataset). At each iteration of the SFS process, each classifier in the pool of candidate classifiers is evaluated and the one that optimizes the performance of the ensemble is kept. The results presented show that there always exists at least one sub-forest that significantly outperforms the initial one, sometimes with ten times less trees. The performance of the RF could therefore be improved by removing from the ensemble well selected trees. The idea with FRF is to avoid the induction of trees that could make the forest performance decrease, by forcing the algorithm to grow only trees that would suit to the ensemble already grown. |
| In this proposed system that the FRF induction could benefit from adopting a parallel approach, that is to say by making the tree induction dependent of the ensemble under construction. For that purpose, it is necessary to guide the tree induction by bringing to the process some "information" from the sub-forest already built. To do so, the idea behind the Fast Random Forest (FRF) algorithm is to perform a resampling of the training data that is halfway between bagging and boosting : proceed first to a random sampling with replacement of N instances, where N stands for the initial number of training instances (bagging), and then reweight the data (some kind of boosting). The reason for this choice is to keep using the two efficient randomization processes (i.e. bagging and Random Feature Selection) of Breiman's RF, and to improve RF accuracy by using the adaptive resampling principle of boosting. |
| Principal Component Analysis is then used to rotate each obtained subsample. Finally, the principal components are rearranged to form the dataset that is used to train a single ensemble member. The first two steps provide the required diversity of the constructed ensemble. |
| A tree can be "learned" by splitting the source set into subsets based on an attribute value test. This process is repeated on each derived subset in a recursive manner called recursive partitioning. The recursion is completed when the subset at a node has all the same value of the target variable, or when splitting no longer adds value to the |
| Employing dimensionality reduction to a training set has the following advantages: |
| • It reduces noise and de-correlates the data. |
| • It reduces the computational complexity of the classifier construction and consequently the complexity of the classification. |
| • It can alleviate over-fitting by constructing combinations of the variables. |
| These points meet the accuracy and diversity criteria which are required to construct an effective ensemble classifier and thus render dimensionality reduction a technique which is tailored for the construction of ensemble classifiers. |
RESULTS AND DISCUSSIONS
|
| A. Experimental Results: |
| In order to evaluate the proposed approach, WEKA framework is used. Proposed approach is tested on3 datasets from the UCI repository which contains benchmark datasets that are commonly used to evaluate machine learning algorithms. |
| B. Performance Metrics: |
| The performances of ensembles are related to the individual accuracy of the base learning algorithms. Comparing ensemble algorithms over these concepts gives us deep understanding of the dynamics of the algorithms compared. The measures to be used for this purpose are as follows: |
| • Kappa value |
| • AUC ( Area under the concentration-time curve) |
| • Time |
Kappa value:
|
| Average Kappa Value of Base Learners (KP). Margineantu and Dietterich suggested a pair wise diversity measure called Kappa. Pair wise diversity was chosen because “diversity” is well defined for two base classifier decisions. Kappa evaluates the level of agreement between two classifier outputs while correcting for chance. |
| For c class labels, Kappa (K) is defined on the c confusion matrix M [11]. The value Mks represents the number of samples with which one of the classifiers predicts sample labels as k, while the other predicts them as s. The value N is the total number of samples. The agreement between two classifier outputs is given by. In the proposed work, the diversity of each base learner is found as |
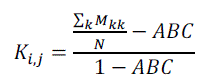 |
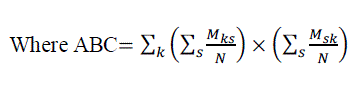 |
| Because the definition of diversity is defined for only two classifiers, one of the classifiers is accepted as one base learner, and the other one is accepted as the majority voted decision of all the base learners except the used one. So for each base learner, the diversity is defined in terms of the difference from all other base learners in means of their decisions. The averaged kappa value of base learners in an ensemble (KP) is the kappa value of the ensemble. The higher KP values show lower diversity because Kappa evaluates the level of agreement between classifier outputs in an ensemble. |
AUC (Area under the concentration-time curve)
|
| Average Individual Accuracy of Base Learners (AIA). To measure base learners’ accuracy, out of bag samples are used. The bagging size is equal to the training size. Each base learner is trained with a different data set and then tested with out of bag samples. For an ensemble having T base learners, the mean value of these T accuracy values is used as the average individual accuracy of base learners. Accuracy of Ensemble (AE). The accuracy of ensembles is calculated with 5 2 cross validation. |
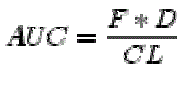 |
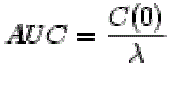 |
| AUC= Area under the concentration-time curve. F = bioavailability, D = dose, CL= clearance, C(0) = extrapolated plasma concentration at time 0, λ = elimination rate constant = CL/Vd. |
| The average of these values is used as an accuracy of ensembles. If an ensemble algorithm generates very similar training sets for its base learners, the average accuracy of base learners may be high. The average accuracy of base learners is indirectly proportional to the diversity of an ensemble. The success of an ensemble is related to these two concepts. None of them can alone guarantee the success of an ensemble. The numerical evidences on these relations are given in succeeding sections. |
CONCLUSION
|
| In this paper a new method has been proposed for inducing Random Forest (RF) classifiers, named Fast Random Forest (FRF). It is based on a sequential procedure that builds an ensemble of random trees by making each of them dependent on the previous ones. This fast aspect of the FRF algorithm is inspired by the adaptive resampling process of boosting. The FRF algorithm exploits the same idea and combines it with the randomization processes used in "classical" RF induction algorithms. A novel method for generating ensembles of classifiers has been proposed. It consists in splitting the feature set into K subsets, running principal component analysis (PCA) separately on each subset and then reassembling a new extracted feature set while keeping all the components. The data is transformed linearly into the new features. A decision tree classifier is trained with this data set. Different splits of the feature set will lead to different rotations and finally accuracy is calculated. Thus high level of accuracy is obtained by using Fast Rotation Forest. |
| |
Tables at a glance
|
 |
 |
 |
 |
| Table 1 |
Table 2 |
Table 3 |
Table 4 |
|
| |
Figures at a glance
|
 |
| Figure 1 |
|
| |
References
|
- L.I. Kuncheva and C.J. Whitaker, “Measures of Diversity in Classifier Ensembles and Their Relationship with the Ensemble Accuracy,” Machine Learning, vol. 51, no. 2, pp. 181-207, 2003.
- Shlens, Jonathon. "A tutorial on principal component analysis." arXiv preprint arXiv:1404.1100 (2014)..
- Barros, Rodrigo Coelho, et al. "A survey of evolutionary algorithms for decision-tree induction." Systems, Man, and Cybernetics, Part C: Applications and Reviews, IEEE Transactions on 42.3 (2012): 291-312.
- Yang, Jing, et al. "Predicting Disease Risks Using Feature Selection Based on Random Forest and Support Vector Machine."Bioinformatics Research and Applications.Springer International Publishing, 2014. 1-11..
- T.K. Ho, “The Random Subspace Method for Constructing Decision Forests,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 20, no. 8, pp. 832-844, Aug. 1998.
- L. Breiman, “Random Forests,” Machine Learning, vol. 45, no. 1, pp. 5-32, 2001.
- J.J. Rodriguez and C.J. Alonso, “Rotation-Based Ensembles,” Proc. 10th Conf. Spanish Assoc. Artificial Intelligence, pp. 498-506, 2004.
- Amasyali, M. Fatih, and Okan K. Ersoy."Classifier Ensembles with the Extended Space Forest." IEEE Transactions on Knowledge and Data Engineering 26.3 (2014): 549-562.
- L. Rokach, “Taxonomy for Characterizing Ensemble Methods in Classification Tasks: A Review and Annotated Bibliography,” Computational Statistics & Data Analysis, vol. 53, no. 12, pp. 4046- 4072, 2009.
- J.J. Rodriguez, C.J. Alonso, and O.J. Prieto, “Bias and Variance of Rotation-Based Ensembles,” Proc. Eighth Int’l Conf. Artificial Neural Networks: Computational Intelligence and Bioinspired Systems, pp. 779-786, 2005.
- J.J. Rodriguez, L.I. Kuncheva, and C.J. Alonso, “Rotation Forest: A New Classifier Ensemble Method,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 28, no. 10, pp. 1619-1630, Oct. 2006.
- L.I. Kuncheva and J.J. Rodr?´guez, “An Experimental Study on Rotation Forest Ensembles,” Proc. Seventh Int’l Conf. Multiple Classifier Systems, pp. 459-468, 2007.
- Tsang, Smith, et al. "Decision trees for uncertain data." Knowledge and Data Engineering, IEEE Transactions on 23.1 (2011): 64-78.
- C.-X. Zhang and J.-S.Zhang, “A Novel Method for Constructing Ensemble Classifiers,” statistics and Computing, vol. 19, no. 3, pp. 317-327, 2009.
- Abdi, Hervé, and Lynne J. Williams. "Principal component analysis." Wiley Interdisciplinary Reviews: Computational Statistics 2.4 (2010): 433-459..
|