INTRODUCTION
|
| While automated conversation recognition has become useful and realistic in everyday life as well as an essential enabler for other modern,technological,innovation,conversation,recognition,precision is far from adequate to assurance a constant efficiency. It can be seriously deteriorated when speech is exposed to preservative appears to be. Though conversation may experience various kinds of appears to be, the work described in this thesis issues one of the most challenging problems in robust speech recognition: crime by an interfering conversation indication with only one direction of information. This issue is especially challenging because the acoustical features of the desired conversation indication are easily puzzled with those of the interfering covering up indication, and because useful details associated with the place of the audio resources is not available with only one direction. The objective of this thesis is to restore the focus on part of conversation combined with interfering conversation, and to enhance the recognition precision that is acquired using the recovered conversation indication. While we will achieve this by mixing several kinds of temporal features, the major novel strategy will be to manipulate immediate frequency to expose the actual harmonic components of a complicated listening to field. The proposed algorithm ingredients immediate regularity from each narrow-band regularity direction using short-time Fourier research. Pair- sensible cross-channel connections depending on instantaneous frequency are acquired for each period of your energy and effort, and groups of regularity elements that are considered to be part of a typical resource are originally identified on the basis of their mutual crosscorrelation. In the thesis, several techniques are mentioned to be able to obtain better reports of immediate regularity. Traditional and graph-cut algorithms are confirmed to gather effectively the design used to recognize the actual harmonic structures. As a supporting means to increase the greatest efficiency, a computationally efficient test for voicing is recommended. Presenter recognition and message recognition are also presented to improve further the greatest efficiency. |
| An calculate of the focus on indication is eventually acquired by renovation using inverse short-time Fourier research depending on chosen elements of the combined alerts. The recognition precision acquired in circumstances of speech-on-speech covering up is evaluated and compared to the corresponding efficiency of conversation recognition systems using previous approaches. The significance of reverberation to the outcome is reliant upon the program of the criteria. For programs such as ASR, the resulting distortions may be unwanted because many conversation databases are not qualified on reverberant conversation. However, Zurek notes that reverberation makes a significant participation to the timbral and spatial features of a identified audio. Thus reverberation may be essential for programs such as listening to field reconstruction (i.e. the splitting and following adjustment or reconfiguration of spatial listening to objects). With so many potential applications for resource splitting, each with a little bit different specifications, it is essential that the evaluation process continues to be separate of application and maintains a common understanding on which techniques may be in evaluation. Furthermore, when considering reverberant circumstances, it is suitable for a measurement to evaluate the splitting efficiency of the algorithm in the reverberant circumstances, without evaluating the effect of the reverberation on the outcome. A latest study has recommended a measurement for evaluating the separation of reverberated conversation. The measurement, known as direct-path, early reflects, and reverberation of focus on and masker (DERTM), measures the reduction of the immediate audio, beginning insights and late reverberation of both the focus on and interfering appears to be. This is because suppressing delayed reverberation is an essential objective for a binary mask if human efficiency in conversation intelligibility is to be obtained. |
| The metric is shown to be very effective for reverberated conversation, but this limits its program, since conversation is not actually the only signal that might need to be produced (musical device splitting is also a typical task). Furthermore, it symbolizes that intelligibility is the greatest objective for resource splitting, which, as mentioned above, may or may not be the case. A typical objective for resource splitting algorithms—and the goal proposed for computational listening to field research (CASA) by Wang —is to calculate the IBM. |
EXISTING METHOD
|
| Adopting the IBM as the computational objective, we can describe precisely sound splitting as binary category. Recommended an beginning monitored category strategy for IBM evaluation although the strategy used binaural features for conversation splitting. Many research implement binary classification for IBM evaluation in the monaural sector. Handled the recognition of disturbance elements in a spectrogram as a Bayesian category issue for robust automatic conversation recognition. Weiss and Ellis utilized relevant vector gadgets to categorize T-F designs. Jin and Wang qualified multilayer perceptrons (MLP) to categorize T-F units using pitch-based features. Their program acquires good separation results in reverberant circumstances. Kim et al. [20] used Gaussian combination designs (GMM) to understand the submission of amplitude modulation variety (AMS) features for target-dominant and interference-dominant designs and then categorized T-F units by Bayesian category. Their classifier led to speech intelligibility developments for normal-hearing audience. Kim and Loizou further recommended an step-by-step training procedure to enhance conversation intelligibility, which begins from a small initial design and up-dates the design factors as more data become available. We recommended a assistance vector machine (SVM) centered program and used both pitch-based and AMS features to categorize T-F designs simplest way of design category is binary (or 2 class) design classification. Cognitive stereo represents wi-fi architectures in which a interaction program does not function in a set allocated group, but rather searches and discovers an appropriate group in which to function. This symbolizes a new paradigm for variety usage in which new gadgets can opportunistically feed on groups that are not being used at their moment and place for their main purpose [5]. |
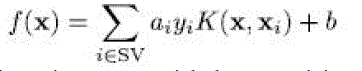 |
| the main program might have a recipient vulnerable to additional disturbance while at the same time the main signals are shadowed enroute to the additional user .However, essential theoretical questions remain as to the actual specifications for engineering a realistic intellectual stereo program so that they do not intervene with the primary users. Presenting the tradeos and difficulties experienced by intellectual receivers can be found . In particular, to ensure non-interference with main customers without being limited to very low transfer abilities, the intellectual stereo program needs to be able to recognize the existence of very poor main alerts, Furthermore, we display that the essential boundaries on moment sensors become hard limits on any possible sensor if the stereo has a limited powerful variety on its feedback.. This paper presents methods that require only a small training corpus and can generalize to unseen conditions. This is inspired by actual dimensions displaying that most of the allocated variety is vastly under utilized . One of the most important factor for any intellectual stereo program is to offer a guarantee that it would not intervene with the main transmitting. To be able to provide such a assurance it is apparent that a intellectual stereo program should be able to recognize the presence of the main indication, to which it might be seriously shadowed. This is a edition of the invisible international airport issue. |
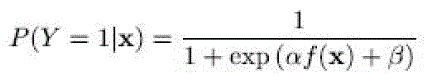 |
| Proposed separating method 2.1 Sinusoidal model Each presenter let is denoted by sj(n) with j [1, 2] and their combination is shown by z(n) with n = 0,1 . . . ,N − 1 as time example catalog where N is the window duration in examples. The sinusoidal design of conversation in a set indication frame Sinusoidal Modelling and Parameter Estimation We consider two variations on unconstrained sinusoidal design developed. The variations we created are described as follow; 1) the spectral coefficients are converted to Mel range to take into consideration the logarithmic sensitivity of individual hearing program, and 2) at each Mel group, the spectral peak with the biggest plenitude is chosen. By utilizing these two fundamentals as our sinusoidal parameter evaluation concept, we discover one optimum per group and end up with three M × 1 vectors of plenitude, regularity and stage for each speaker signal or their combination. We obtain mixture estimator depending on unconstrained sinusoidal factors of the actual speakers and their combination. The research conducted in the past section demonstrated that analytics depending on SNR cannot offer a regular ranking for a given binary cover up when convolutional disturbances are presented. It is therefore appropriate to discover a measurement that can offer a consistent score for a given binary cover up individually of convolutional disturbances. Hence, if calculating the IBM is the objective of resource separation algorithms that utilize binary covers, then a measurement that quantifies the level to which a measured cover up is perfect should be a suitable choice. Furthermore, findings created by Li and Loizou point out that the design of the binary cover up is more essential for speech intelligibility than the regional SNR of each T–F device because the pattern of the cover up may help to their research confirmed a powerful negative correlation between binary cover up mistake and conversation intelligibility. This implies that, at least for anechoic conversation, calculating the binary mask error can estimate the conversation intelligibility of a binary cover up. When evaluating the perfect and measured covers, each T–F unit from the measured cover up can be immediate hearing interest. This indicates that the measurement should consider the design of the cover up without weighting the efforts of each T–F device according to its regional SNR. Such a measurement was suggested by Hu and Wang. Their metric assesses segmentation efficiency and is depending on a measurement proposed by Machine etal.For evaluating picture segmentation. Hu and Wang’s measurement analyzes perfect sections with measured |
| Sections. Consequently, in their strategy there are several results of the comparison; sections can be recognized as: |
| Correct: The measured and perfect sections considerably overlap |
| Under-segmented: A measured section includes two or more ideal segments |
| Over-segmented: An perfect section includes two or more calculated segments |
| Mismatch: The measured section considerably includes a T–F region from the perfect qualifications. |
| Missing: The measured section absolutely includes a T–F region belonging to the perfect qualifications. |
| However, not all methods utilize segmentation in this way and hence this measurement may not be employable by all methods. The above mentioned research conducted by Li and Loizou demonstrated the consequences on conversations intelligibility of binary cover-up mistake i.e, the either appropriate (if it suits the corresponding device in the perfect mask) or wrong in one of two methods. Cases where the perfect focus on is wrongly recognized may, in a worst situation situation, outcome in an essential focus on resource device not contributing to the outcome. Situations where the perfect qualifications is incorrectly recognized may outcome, in a most severe situation, in masking of the resource by the interferer or other disturbance. Li and Loizou discover that for conversation intelligibility incorrect alert mistakes are more detrimental than skip mistakes. |
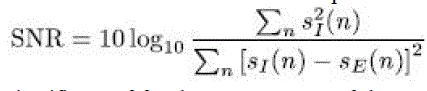 |
| Scientific proof for the consequences of these two mistake kinds in other programs has not been discovered but the comparative importance of each mistake kind may well be application– specific, with skip mistakes being more essential in some applications where conversation intelligibility is not the main objective. Therefore to determine the measurement, and to maintain its freedom of program, both mistakes are here calculated similarly. Observe that this could be adapted to fit a particular program by modifying the mistake weighting to be more delicate to either mistake kind. Consequently, the perfect binary cover up rate (IBMR) is suggested as a measurement for evaluating resource separating methods that utilize binary masks. IBMR is an tailored and generalized way of binary mask error or labelling precision. IBMR provides an intuitive score in the period [0,1] for a cover up, depending on its correspondence to the IBM, rather than evaluating the resynthesised outcome. |
PROPOSED METHOD
|
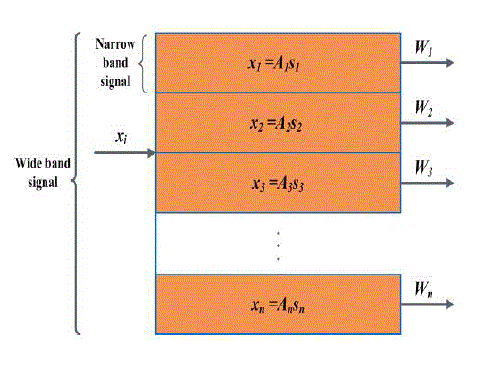
| INDEPENDENT COMPONENT ANALYSIS (ICA): Independent Component Analysis (ICA) was originally proposed to solve the blind signal or source separation problem of recovering independent source signals (e.g., music, speech, different voice and noise sources) after they are linearly mixed by an unknown matrix, A (Figure 1).There are only N dissimilar recorded mixtures but nothing is known about the mixing process or about sources. The task is to recover a version, S, identical save for scaling and permutation, U, of the original sources by finding a square matrix, W, specifying spatial filters that linearly invert the mixing process, i.e. U=WX. Bell and Sejnowski (1995) have proposed a simple neural network algorithm by using infomax the mixtures of independent sources are blindly separated.They show that maximizing the joint entropy, H(y), of the output of a neural processor minimizes the mutual information among the output components. Following their notations, each input vector, x(t), represents an observable vectors recorded from all the input channels at time t. Hence maximization of joint entropy is executed . |
ICA applied to speech signals :
|
| Independent Component Analysis tries to decompose a multivariate signal into no of independent non-Gaussian signals. As an example, sound is usually a signal that is composed of the numerical addition, at each time t, of signals from several sources. The main problem arises that whether it is possible to separate these contributing sources from the observed total signal. When the statistical independence assumption is correct, blind source of ICA separation of original and noise signals which are combined and provides very desirable results. It is also used for signals that are not supposed to be generated by a mixing for analysis purposes. A important application of ICA is the cocktail party problem when two or more persons talking simultaneously in a room if inorder to find out the individual speech cleanly by eliminating the unseen noise. Meanwhile by supposing the no echoes or time delays the problem can be simplified. An important annotation is to consider is that if N sources are present, at least N observations (e.g. microphones) are needed to recover the original signals. This constitutes the square case (J = D, where J is the dimension of the model and D is the input dimension of the data). Other cases of underdetermined (J > D) and over determined (J < D) have been investigated. |
| Hence that the ICA separation of combined signals which are the combination of original and noise speech gives very fair results are depending upon two assumptions that are to be made 1).The source signals must be independent of each other.2)The values in each source signal have non-Gaussian distributions. |
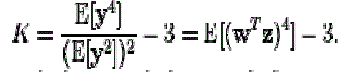 |
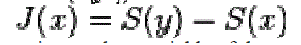 |
| y is a Gaussian random variable of the same covariance matrix as x |
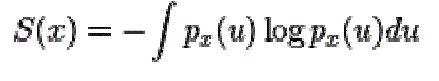 |
| An approximation for negentropy is |
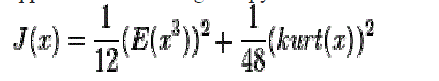 |
| A proof can be found on page 131 in the book Independent Component Analysis written by signal.(They contribute great works to ICA).This approximation also suffers the same problem as kurtosis (sensitive to outliers). Other approaches were developed. |
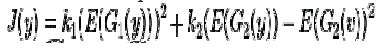 |
| A choice G1 of and G2 are |
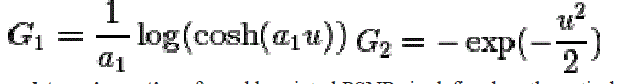 |
| Peak signal-to-noise ratio, often abbreviated PSNR, is defined as the ratio between the maximum possible power of a signal and the power of corrupting noise which affects the fidelity of its representation. Normally, PSNR is denoted in terms of logarithmic decibal scale |
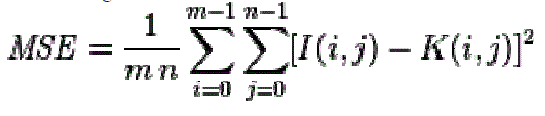 |
| The PSNR (in dB) is defined as: |
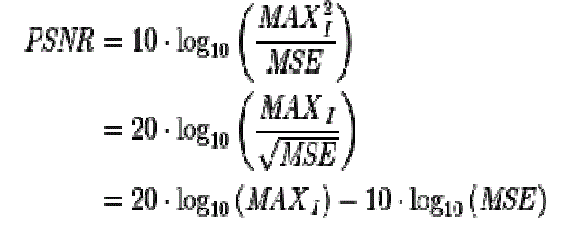 |
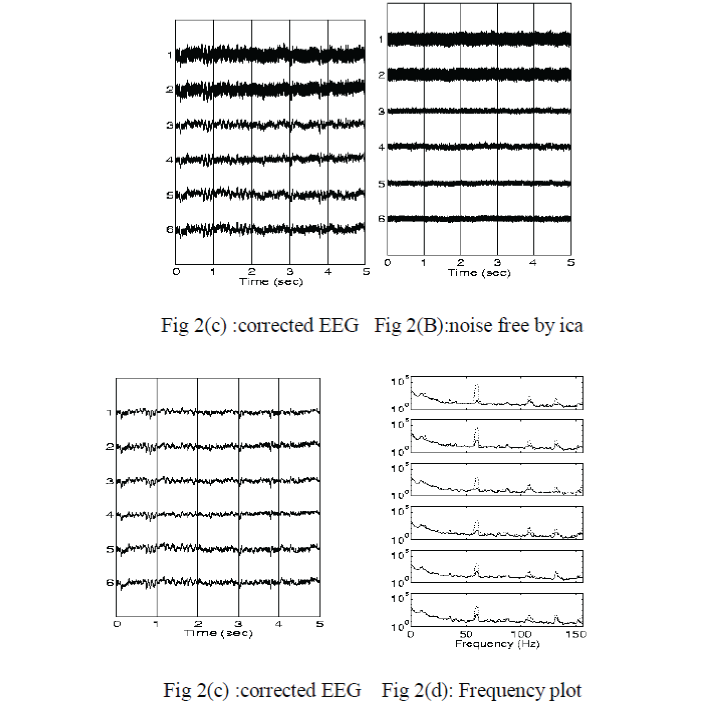
| ICA applied to EEG signals: |
| ICA solves a different problem from brain activation localization,as the method provides information on when a nueral source is active, not on where it is loated.the ICA method does ,however, provide a scalp distribution of the stationary electric field produced by each neural source(Makeig et al,1997). |
EXPERIMENTAL RESULTS
|
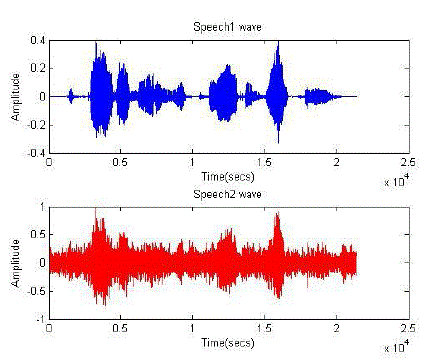 |
| Fig1: original speech |
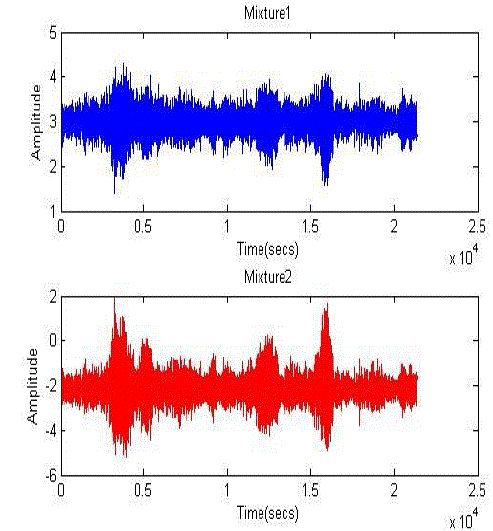 |
| F ig2: Mixed speech |
 |
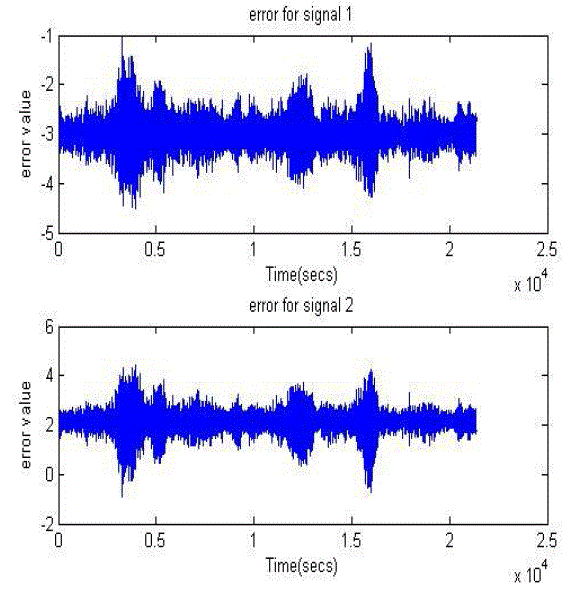
| Fig 3: Error signal |
 |
| Fig 4: ICA output speech |
COMPARISION
|
| It has been observed that the proposed method ICA improves the peak signal to noise ratio(PSNR) compared to general one. Hence SNR is improved by 10 db to 15 db when compared to the previous method. |
CONCLUSION
|
| This paper presents a fully scalable heterogeneous building for the acceleration of the ICA classification. Here the proposed scheme increases the SNR value and clean output speech can be obtained under unseen noise conditions. Additionally, SNR is improved by 10db to 15 db by our proposed method and hence a better peak signal to noise ratio(PSNR) can be obtained by using the ICA classification. Hence the technique is evaluated for different type of mixture signals which showed that original speech signal is obtained by eliminating the noise. |
Figures at a glance
|
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
|
References
|
- Shilton, M. Palaniswami, D. Ralph and A. C. Tsoi. Incremental Training of Support Vector Machines. IEEE Transactions on Neural etworks, vol. 16, no. 1, page 114{131, Jan 2005.
- Shilton, D. Lai and M. Palaniswami. A Monomial SV Method For Regression. Submitted to PAMI, 2004.CONFERENCE PROCEEDINGS.
- Shilton, M. Palaniswami, D. Ralph and A. C. Tsoi. Incremental Training of Support Vector Machines.Proceedings of International Joint Conference on Neural Networks, IJCNN'01 (CD version), 2001.
- Shilton and M. Palaniswami. A Modi_ed _-SV Method for Simpli_ed Regression. Proceedings of the International Conference on Intelligent Sensing and Information Processing, page 422{427, 2004.
- M. Palaniswami, A. Shilton, D. Ralph and B. D. Owen. Machine Learning using Support Vector Machines.Proceedings of International Conference on Artificial Intelligence in Science and Technology, AISAT2000, 2000.
- M. Palaniswami and A. Shilton. Adaptive Support Vector Machines for Regression. Proceedings of the 9th International Conference on Neural Information Processing, vol. 2, page 1043{1049, November 2000.
- D. Lai, A. Shilton, N. Mani and M. Palaniswami. A Convergence Rate Estimate for the SVM Decomposition Method. Proceedings of the International Joint Conference on Neural Networks, IJCNN05, page 931{936, August 2005.
- S. Challa, M. Palaniswami and A. Shilton, Distributed data fusion using Support Vector Machines. Proceedings of the Fifth International Conference on Information Fusion, vol. 2, page 881{885, July 2002.
|