Keywords
|
| Quantum Computing, Quantum Error Correction, Quantum Model, BQSM |
INTRODUCTION
|
| Quantum computation means the study of the information processing tasks that can be accomplished using quantum mechanical systems. This quantum security model is planned to explore error correction in quantum based systems. Next generation computers are expected to start popularizing the use of quantum logic circuits and quantum algorithms by bringing out desktop systems that use quantum logic. ln this context it is necessary to have schemes that protect quantum information from errors due to de coherence and other quantum noise' This quantum error correction is also essential to achieve fault-tolerant quantum computation (essential for quantum based security schemes) that can deal not only with noise on stored quantum information, but also with faulty quantum gates, faulty quantum preparation and faulty measurements. ln classical error correction redundancy exists. The typical reported way is to store the information multiple times, and if these copies are later found to disagree (similar to a majority vote) then the error is detected'. This approach is effective for single bit errors rather than multiple bit errors. However, in the case of quantum information copying is prohibited due to the no-cloning theorem and this presents an obstacle to formulating a theory of quantum error correction. It is planned to explore the concept of spreading the information of one qubit onto a highly-entangled state of several (physical) qubits. Thus, a quantum error correcting code by storing the information of one qubit onto a highly-entangled state of multiple qubits is to be explored. ln this way, a quantum error correcting code protects quantum information against errors of a limited form. |
| One opportunity to create unconditionally secure quantum commitment and quantum oblivious transfer (OT) protocols is to use the bounded quantum storage model (BQSM). In this model, we assume that the amount of quantum data that an adversary can store is limited by some known constant Q. To inflict any limit on the amount of classical (i.e., nonquantum storage model) data the adversary may store. In the BQSM, one can build commitment and oblivious transfer protocols. The underlying idea is the following: The protocol parties exchange more than Q quantum bits (qubits). Since even a dishonest party cannot store all that information (the quantum memory of the adversary is limited to Q qubits), a large part of the data will have to be either measured or discarded. Forcing dishonest parties to measure a large part of the data allows circumventing the impossibility result by Mayers commitment and oblivious transfer protocols can now be implemented. |
| The advantage of the BQSM is that the assumption that the adversary's quantum memory is limited is quite realistic. With today's technology, storing even a single qubit reliably over a sufficiently long time is difficult. An extension of the BQSM is the noisy-storage model introduced by Wehner, Schaffner and Terha.Instead of considering an upper bound on the physical size of the adversary's quantum memory, an adversary is allowed to use imperfect quantum storage devices of arbitrary size. The level of imperfection is modelled by noisy quantum channels. For high enough noise levels, the same primitives as in the BQSM can be achieved and the BQSM forms a special case of the noisystorage model. |
RELATED WORK
|
| The theory of quantum mechanics was prompted by the failure of classical physics in explaining a number of microphysical phenomena that were observed at the end of nineteenth and early twentieth centuries . Now, quantum mechanics is vital for understanding the physics of solids, lasers, semiconductor and superconductor devices, plasmas, etc. In recent years, quantum mechanics has been connected with computer science, information theory in communication and digital signal processing. For example, Shor has showed that integer factoring could be done in polynomial time on a quantum computer. One of major applications of Shor’s quantum factorization algorithm is to break RSA public key cryptosystems. Thus, developing new computing methods and signal processing algorithms by borrowing from the principle of quantum mechanics is a very interesting and new research topic. Quantum computing is a new approach to computation that has the possibility to revolutionize the field of computer science. The late Nobel Prize winning physicist Richard Feynman, who was interested in using a computer to simulate quantum systems. |
| Measurement: A measuring apparatus determines properties of a quantum system by interacting with it in some way. Consequently, it is impossible to treat either the system or the apparatus as isolated, at least during the crucial time period when they interact. Instead, one should regard both together as constituting a single combined and isolated quantum system to which the corresponding unitary time development operators application. |
| Quantum information types: Since the world (so far as we know) is quantum mechanical, “classical” information must be some sort of “quantum information. Species of quantum information which represents at least one way of seeing how quantum information theory is connected to classical information theory as developed by Shannon and his successors, and in what way new phenomena arise when quantum effects are taken into account. |
| Quantum error correction was developed in analogy with classical error correcting codes, but in the quantum case one needs a few additional tricks. Classical error correction is based on redundancy making several copies of information in different signals or different physical objects, so that if one or a few of these are lost or corrupted, The original information can be recovered from the ones that remain. Quantum error correction is based on the same general principle, but simply copying the information in the classical sense will not work, in view of no-cloning arguments. |
| Dense Coding: The phenomenon of “dense coding” is based on the observation that given some state belonging to the Bell basis. There are local unitaries on Ha which will map it onto any of the other states belonging to the basis, apart from an overall phase. There are similar unitaries on Hb. |
EXISTING METHODOLOGY
|
| A single bit errors are store the information multiple times, later found to disagree (similar to a majority vote) then the error is detected' and multiple bit errors are case of quantum information copying is prohibited due to the no-cloning theorem. An information of one qubit onto a highly-entangled state of several (physical) qubits and protects quantum information against errors of a limited form. |
PROPOSED METHODOLOGY
|
| Quantum security model is proposed a new methodology is classical error correcting scheme a syndrome measurement is planned to diagnose which error corrupts an encoded state. The corrective operation is then applied using a reversible operation to retrieve the true information. A multi-qubit measurement that does not disturb the quantum information in the encoded state but retrieves information about the error is to be done. A syndrome measurement can determine whether a qubit has been corrupted, and if so, which one. lt is required that the outcome of this operation (the syndrome) should reveal not only which physical qubit was affected, but also, in which of several possible ways it was affected. A qubit (or Quantum BIT) is a standard 'bit' - it is a memory element. It can hold not only the states '0' and '1' but a linear superposition of both states, Advantage of Quantum computation model first one is called as bit flip is referred in quantum as x-measurement and second is sign flip is referred in quantum as z-measurement and finally combination of bit flip and sign flip. |
ARCHITECTURE OF QUANTUM COMPUTING MODEL
|
| Quantum computer architecture has much to learn from classical computer architecture, it is difficult to tease apart the intertwined issues of the workload for a system, and the design of the system itself. In fact, workload, technology, error correction and architecture must all comes together to create a complete system. Most of us have been using Shor’s algorithm as a benchmark, both for its importance and clarity, and because the arithmetic and quantum Fourier transform on which it is founded are valuable building blocks for other algorithms, as well. |
| An initiation of quantum error correction, many researchers believed that these problems were insurmountable or at least limited the range of problems to which quantum computing can be applied.Without error correction (both theory and practice), the machines cannot run for any useful length of time. At the “bottom” of the stack lie the qubit storage, which are providing useful proving grounds for quantum theory itself, but are of interest here primarily as the foundation for building large-scale quantum computers. Both the top and bottom of this stack are heavily populated with brilliant, dedicated researchers. |
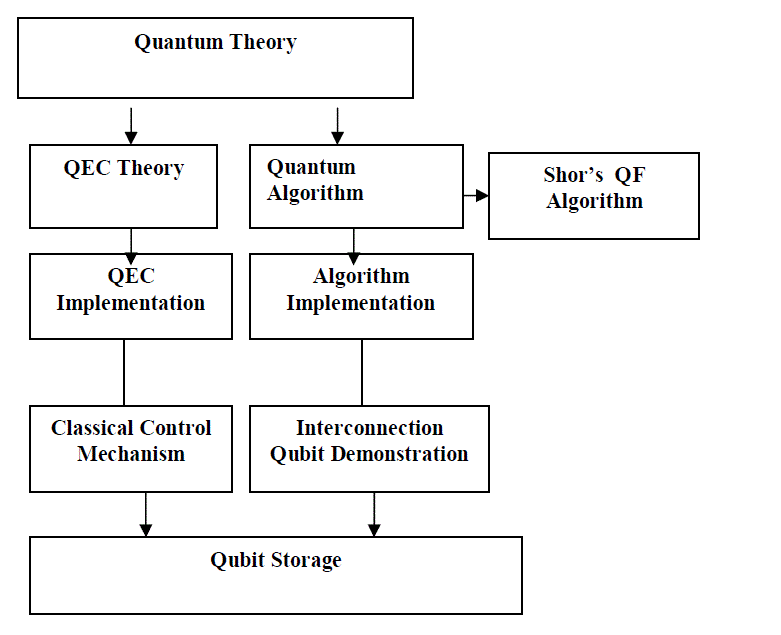
| The figure 1.shows constituting the realm of quantum computing architecture, are less heavily populated. Designing architecture is the process of choosing the metrics for success, defining the desired performance and the costs for components so that they may be balanced as desired. Functionality is divided into subsystems, and the interfaces between subsystems defined, along with corresponding promises and assumptions about behavior or conditions maintained. Likewise quantum computers will be much more than simply uniform collections of qubits. |
| In classical systems, we frequently use multiple levels of error correction. The same principle can be applied in quantum systems, in a manner called concatenation. In a concatenated system, physical qubits are grouped to encode a logical qubit, and a group of logical qubits is further encoded (using the same or a different code) to provide greater protection against errors. |
| Quantum algorithms initiate by placing one input register in this superposition. This effect allows a quantum computer to calculate a function on all possible inputs at the same time, in a single pass. Shor’s Algorithm is an algorithm consists of both classical and quantum portions, with the quantum portion being a period-finding method based on the QFT and arithmetic to calculate the modular exponentiation of two integers.A quantum algorithm for integer factorization. Given an integer N, find its prime factors. On a quantum computer to factor an integer N, Shor's algorithm runs in polynomial time (the time taken is polynomial in log N, which is the size of the input). Specifically it takes time O((log N)3), demonstrating that the integer factorization problem can be efficiently solved on a quantum computer. This is significantly faster than the most efficient known classical factoring algorithm. The efficiency of Shor's algorithm is due to the efficiency of the Quantum Fourier Transform(QFT), and modular exponentiation by repeated squarings. Shor's algorithm shows that factoring is efficient on an ideal quantum computer. |
| Shor's Factoring Algorithm contains two parts: |
| 1. A reduction, which can be done on a classical computer, of the factoring problem to the problem of orderfinding. |
| 2. A quantum algorithm to solve the order-finding problem. |
| Algorithm: |
| 1. Pick a random number a < N. |
| 2. Compute gcd(a, N). This may be done using the Euclidean algorithm. |
| 3. If gcd(a, N) ≠ 1, then there is a nontrivial factor of N, so we are done. |
| 4. Otherwise, use the period-finding subroutine (below) to find r, the period of the following function: f(x) = ax mod N. i.e. the order r of ain (ZN)X , which is the smallest positive integer r for which f(x+r)=f(x) or f(x+r)=ax+r, mod N= ax mod N. |
| 5. If r is odd, go back to step 1. |
| 6. If ar/2 ≡ −1 (mod N), go back to step 1. |
| 7. gcd(ar/2 ± 1, N) is a nontrivial factor of N. We are done. |
CONCLUSION AND FUTURE SCOPE
|
| Quantum technologies will play a very important role in the future and already to date, several companies are commercializing quantum communication systems. In the future [a quantum computer] could do all sorts of things. A quantum computer [would have] massive processing power because it can do computational tasks in parallel and can solve problems which are virtually intractable using an ordinary computer. Quantum computers are very good at search problems and also for finding the primes of large numbers, which is an important area for cryptography. Also this is going to be one of the great discoveries of the 21st century as these computers will use the techniques of Quantum mechanics and Quantum computing, which will provide more security to the renders for message or information sharing. The proposed method may be implemented in real time applications as it is very simple and the cost may also very less when quantum computer exists. |
| |
Figures at a glance
|
 |
| Figure 1 |
|
| |
References
|
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, 2000.
- Galindo and M. A. Martin -Delgado, Information and computation: Classical and Quantum aspects,” Reviews of Modern Physics, vol.74, April 2002.
- Marinesu ,D.C. and G .M. Marinesu, 2004 . Approaching Quantum Computing.Prentice Hall, Upper Saddle River, NJ.
- Vishal, S., 2007.Quantum Computing.Tata McGraw Hill, Delhi.
- S. Abramsky, High-level methods for quantum computation and information, in: Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science, pp. 410–414.
- Rodney Doyle Van Meter III. Architecture of a Quantum Multicomputer Optimized for Shor’s Factoring Algorithm.PhD thesis, Keio University, 2006. available as a rXiv:quant-ph/0607065
- W. D ¨ur and H.J. Briegel. Entanglement purification and quantum error correction.Rep.Prog. Phys., 70:1381–1424, 2007
|