Keywords
|
| Block Truncation, Digital Halftoning, Dot Diffusion, Error Diffusion. |
INTRODUCTION
|
| Block truncation coding (BTC) was first proposed by Delp and Mitchell in 1989. Block truncation coding is a lossy type of image compression. In block truncation coding (BTC), the original image is divided into fixed-size non overlapping blocks of size M×N. The block size chosen is usually small to avoid the edge blurring and blocking effect. Each block is independently coded using a two level (1-bit) quantizer. The two values preserve the first and the second moment characteristic of the original block. BTC does not provide a higher gain than any of the modern image compressing algorithms like JPEG or JPEG-2000, but it is much lesser complex. |
| Digital Halftoning is a technology of converting a continuous tone image to a two tone image. A continuous tone image and a halftoning image are similar when the low-pass nature of the Human Visual System (HVS) is the perceived device. There are many kinds of halftoning techniques, including ordered dithering, error diffusion, and dot diffusion. |
BLOCK TRUNCATION CODING
|
| Block truncation coding (BTC) was first proposed by Delp and Mitchell in 1989 [1]. As stated earlier, given an image of size P X Q, BTC divides the original image into non overlapped blocks of size M X N. These blocks are processed independently and coded using a two-level quantizer. Thus each block will be transmitted as a set of two values. The first- and second-moment of the block are calculated as |
 eq. (1) eq. (1) |
 eq. (2) eq. (2) |
| The corresponding variance is obtained by |
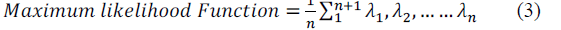 eq. (3) eq. (3) |
| where the variable xij represents the pixel values in the block. BTC is a 1-bit quantizer with threshold, therefore, the bitmap is calculated as |
 eq. (4) eq. (4) |
| and the reconstructed result is given by |
 eq. (5) eq. (5) |
| The variables a and b are given by: |
 eq. (6) eq. (6) |
| and |
 eq. (7) eq. (7) |
| where m = M x N, q denotes the number of pixels greater than and is the number of pixels less than . |
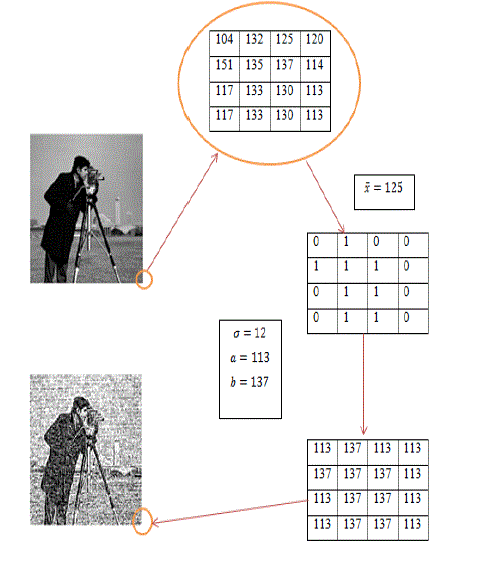 |
| The above figure shows the processing of a block in BTC. The mean is calculated for each block and each pixel in a block is compared to the mean. If the pixel value is greater than the mean, it is recorded as a “1” and if the value is smaller than the mean, it is recorded as a “0” in the bitmap. While converting the bitmap into the final compressed image; for a “0” in the bitmap, it is replaced by the value of “a” which is calculated using eq. 6 and for a “1” in the bitmap, it is replaced by the value of “b” which is calculated using eq. 7. |
BLOCK TRUNCATION CODING USING DIGITAL HALFTONING
|
| Many endeavors have been addressed in the literature to improve the computational complexity, compression ratio, and image quality of the BTC. In [2], the author used the error diffusion technique. Error diffusion enjoys the benefit of diffusing the quantised error into the neighbouring pixels. The error diffusion can effectively diffuse the error between the neighboring pixels and then maintains the average grayscale in a local region. |
| The original image is first divided into M x N blocks. The average value of the block is given by eq. 1. The maximum and minimum are given by: |
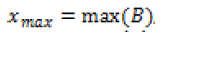 eq. (8) eq. (8) |
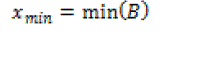 eq. (9) eq. (9) |
| where the B denotes the divided original block. |
| The pixels are processed according to the equations given below: |
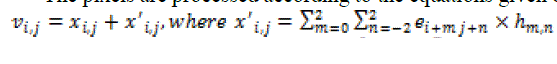 eq. (10) eq. (10) |
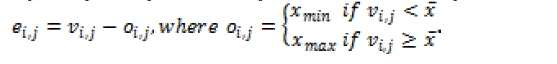 eq. (11) eq. (11) |
| The variable denotes the current input pixel value, and denotes the diffused error sum added up from the neighboring processed pixels. The variable denotes the binary output in position and the error kernel is used to diffuse the error caused by the difference, between the output binary value and the input grey level value. The variable denotes the modified value. EDBTC uses a threshold of 128. |
| In [3], the authors used the void and cluster dithering approach. Using the void-and-cluster halftoning, the image quality is improved when operated in high coding gain applications. The dither array in order dithering is employed to substitute the fixed average threshold in BTC, and the extreme pixel values in a block are adopted to substitute the high mean and low mean. |
| Consider an image of size P x Q ODBTC will divide the image into blocks of size M x N The maximum and minimum values of the block are given by equations 8 and 9 respectively. The size of the dither array is M x N, which the same as the divided block in BTC. ODBTC can be written as |
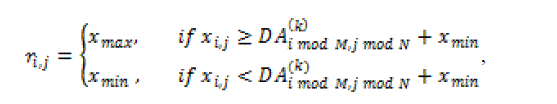 eq. (12) eq. (12) |
where represents the ODBTC result; represents the original image, and 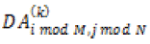 represents void-andcluster dither array, and represents void-andcluster dither array, and 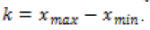 |
| A significant feature of the ODBTC is the dither array lookup table (LUT), where each specific size dither array has its corresponding 255 different scaling versions. The 255 scaling versions are obtained by |
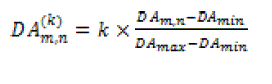 |
where 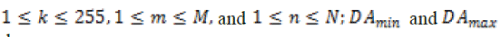 represent the minimum and maximum values in dithered array. represent the minimum and maximum values in dithered array. |
| The dot diffusion method for halftoning, is an attractive method which attempts to retain the good features of error diffusion while offering substantial parallelism. The dot diffusion method for halftoning has only one design parameter, called the class matrix C. It determines the order in which the pixels are processed. Thus, the pixel positions (n1, n2) of an image are divided into IJ classes For example, if we use a class matrix of size I = J = 8, then there will be 64 class members in that class matrix. We then look at the eight neighbours (n1, n2) of and replace each constant tone pixel with an adjusted version for those neighbours which have a higher class number (i.e., those neighbours that have not been processed yet) [4]. |
| DDBTC algorithm [5] is similar to the traditional BTC algorithm with a few changes. This algorithm has two main differences to that of the traditional BTC: |
| 1. The high mean and low mean are replaced by the maximum xmax and xmin minimum in a block. |
| 2. The bitmap generation is done using the dot-diffused halftoning. |
| The maximum and minimum values of the block are given by equations 8 and 9 respectively. Consider an image of size P x Q DDBTC will divide the image into blocks of size M x N These blocks are then independently coded. The order of processing of a pixel in a block is predefined by a class matrix. Each divided block corresponds to the same class matrix. |
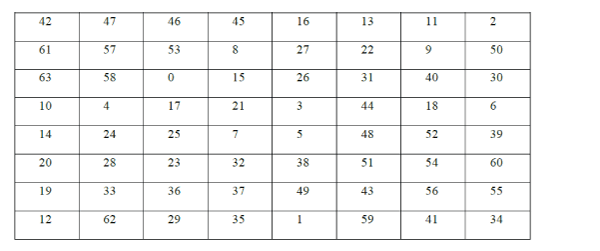 |
| The above table is the class matrix for an 8×8 block which determines the order of processing of pixels which was generated by Guo and Liu in their paper for optimized dot diffusion [5].The pixels numbered “0” will be processed first. |
| The pixels in a block are processed according to the equations given below: |
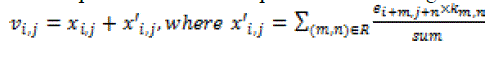 eq. (14) eq. (14) |
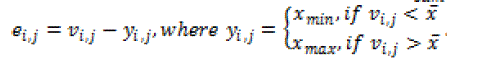 eq. (15) eq. (15) |
| Where the variables , , and are given by equations 1, 8 and 9 respectively. is the input original image pixel, is the diffused error accumulated from the neighboring pixels, and the variable is the processed output pixel. The variable denotes the binary output in the bitmap, and variable denotes the difference between the modified grayscale output and the binary output . The variable denotes the diffused weighting, and denotes the support region [6]. |
| The variable sum is given by: |
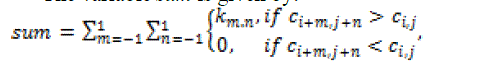 eq. (16) eq. (16) |
| where the variable denotes the coefficient value in the class matrix. |
EXPERIMENTAL RESULTS
|
| The test was conducted on a set of three grayscale images: Cameraman, Tire and Coins. The simulation was carried in MatlabTM. |
| The following figure shows the cropped results of the test images. The images are compressed by both BTC and DDBTC algorithms and the results are displayed for comparison |
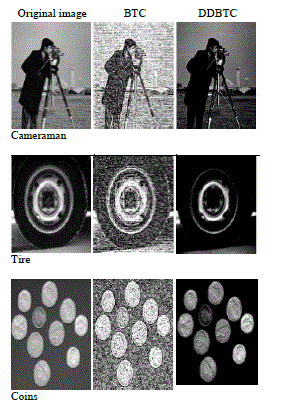 |
| The first column in the above figure shows the thumbnails of the original images, the second column shows the thumbnails of these images compressed by the BTC algorithm, and the third column shows the thumbnails of the same images compressed by the DDBTC algorithm. |
CONCLUSION
|
| This study presented various digital halftoning-based BTC image compression techniques which can provide an excellent image quality and artifact-free results (inherent blocking effect and false contour artifacts of the traditional BTC) simultaneously. |
| Two algorithms were selected namely, the original block truncation coding (BTC) and Dot Diffused Block Truncation Coding (DDBTC) to generate the experimental results. The two algorithms are based on dividing the image into non overlapping blocks. The two techniques were applied to different grey level test image each containing 256×256 pixels. |
| As is evident from the experimental results, the image quality of the DDBTC is superior to BTC. The performance can be attributed to parallel processing of the blocks in the dot diffusion. |
| |
References
|
- E. J. Delp and O. R. Mitchell, “Image compression using block truncation coding,” IEEE Trans. Communications, vol. 27, no. 9, pp. 1335-1342, Sept. 1979.
- J. M. Guo “Improved block truncation coding using modified error diffusion,” Electronics Letters, vol. 44, no.7, pp. 462-464, Mar. 2008.
- Guo and Wu, “Improved Block Truncation Coding based on the Void and Cluster Dithering Approach,” IEEE Transactions on image processing, vol. 18, no. 1, pp. 211-213, Jan. 2009.
- M. Mese and P. P. Vaidyanathan, “Optimized halftoning using dot diffusion and methods for inverse halftoning,” IEEE Trans. ImageProcessing, vol. 9, pp. 691–709, Apr. 2000.
- Guo and liu, “Improved Block Truncation Coding using Optimized Dot Diffusion,” IEEE Trans. Image Processing (To be published in a forthcoming issue of IEEE).
- D. E. Knuth, “Digital halftones by dot diffusion,” ACM Trans. Graph., vol. 6, no. 4, Oct. 1987.
|