Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Self-Learning Optimization Approach to Single Image Super-Resolution using Kernel ridge regression model

Ms. Dharani S
 PG Student (CSE), Sri Krishna College of Engineering and Technology, Anna University, Chennai, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Learning-based approaches for image super-resolution (SR) have attracted the attention from researchers in the past few years. We present a novel self-learning approach with multiple kernel learning for adaptive kernel selection for SR. The Multiple Kernel Learning is theoretically and technically very attractive, because it learns the kernel weights and the classifier simultaneously based on the margin criterion. With theoretical supports of kernel matching search method and Optimization approach (Gradient) are proposed our SR framework learns and selects the optimal Kernel ridge regression model when producing an SR image, which results in the minimum SR reconstruction error. We evaluate our method on a variety of images, and obtain very promising SR results. In most cases, our method quantitatively and qualitatively outperforms bi-cubic interpolation and state-of-the-art learning based SR approaches.

INTRODUCTION
Super Resolution (SR) has been an active research topic in the areas of image processing and computer vision. It is a process to produce a high-resolution (HR) image from one or several low-resolution (LR) images. Conventional methods are based on the reconstruction of multiple LR images, and they approach SR as solving an inverse problem, i.e., they recover the HR image as a linear operation of multiple LR patches. Recently, learning-based SR approaches which focus on modeling the relationship between training low and high-resolution images have also attracted researchers, while the existence of the aforementioned relationship is typically seen in natural images [1], [2]. However, the difficulty of learningbased SR methods lies on the selection of proper training data and proper learning models for SR from an unseen target image.
In machine learning, support vector regression (SVR) [3] is considered as an extension of support vector machine (SVM), which exhibits excellent generalization ability in predicting functional outputs without any prior knowledge or assumption on the training data (e.g., data distribution, etc.). SVR is capable of fitting data via either linear or nonlinear mapping, and the use of SVR has been applied in applications of data mining, bioinformatics, financial forecasting, etc. Previously, SVR has been shown to address SR problems in [1], [4]; however, these SVR-based SR approaches require the collection of training low and high-resolution image pairs in advance, and this might limit their practical uses. In this paper, we propose a self-learning framework for SR. We not only present quantitative and qualitative SR results to support our method, we will also provide theoretical backgrounds to verify the effectiveness of our learning framework.
The remainder of this paper is organized as follows. Prior SR works are discussed in Section II. Section III details the novel self-learning approach with multiple kernel learning for adaptive kernel selection for SR. Section IV provides empirical results on a variety of images with different magnification factors, including comparisons with several SR methods. Finally, Section V concludes this paper.

RELATED WORK

A. Reconstruction-Based SR
Typically, reconstruction-based SR algorithms require image patches from one or several images (frames) when synthesizing the SR output. This is achieved by registration and alignment of multiple LR image patches of the same scene with sub-pixel level accuracy [5]–[7]. For single-image reconstruction-based SR methods, one needs to exploit self similarity of patches within the target LR image. With this property, one can thus synthesize each patch of the SR image by similar patches in the LR version. However, reconstruction-based methods are known to suffer from ill-conditioned image registration and inappropriate blurring operator assumptions (due to an insufficient number of LR images) [8]. Moreover, when an image does not provide sufficient patch self-similarity, single-image reconstruction based methods are not able to produce satisfying SR results [9]. Although some regularization based approaches [5], [7], [10] were proposed to alleviate the above problems, their SR results will still be degraded if only a limited number of low-resolution images/patches are available or if a larger image magnification factor is needed. According to [8], [11], the magnification factor of reconstruction-based SR approaches is limited to be less than 2 for practical applications. A recent approach proposed in [12] alleviates this limitation by learning image prior models via kernel principal component analysis from multiple image frames. Since single-image SR does not require multiple LR images as inputs, it attracts the interest from researchers and engineers due to practical applications. As discussed above, methods assuming the existence of image patch self-similarity need to search for similar patches from an input image when synthesizing the SR output. However, the assumption of selfsimilarity might not always hold, and the associated SR performance varies with the similarity between different categories of image patches. The nonlocal means (NLM) method [13] is one of the representatives which advocates such a property in image related applications.

B. Learning-Based SR
In the past few years, much attention has been directed to learning (or example) based SR methods (e.g., [1], [14], [15]), which can be considered as single image SR approaches utilizing the information learned/observed from training image data. With the aid of training data consisting of low and high resolution image pairs, learning-based methods focus on modeling the relationship between the images with different resolutions (by observing priors of specific image or context categories). For example, Chang et al. [15] applied the technique of locally linear embedding (LLE) for SR purposes. They collected a training data set with multiple low and high-resolution image pairs. For each patch in an input LR image, they proposed to search for similar patches from LR training images, and they used the corresponding training HR patches to linearly reconstruct the SR output (using the weights determined by LLE). Ni et al. [1] proposed to use support vector regression (SVR) to fit LR image patches and the pixel value of the corresponding HR images in spatial and DCT domains. It is not surprisingly that, however, the performance of typical learning-based methods varies significantly on the training data collected. As a result, in order to achieve better SR results, one needs to carefully/manually select the training data. In such cases, the computation complexity of training and difficulty of training data selection should be both taken into consideration.
Recently, Glasner et al. [2] proposed to integrate both classical and example-based SR approaches for single image SR. Instead of collecting training image data beforehand, they searched for similar image patches across multiple down-scaled versions of the image of interest. It is worth noting that this single image SR method advocates the reoccurrence of similar patches across scales in natural images, so that their approach simply downgrades the resolution of the input image and perform example-based SR. In other words, once similar patches are found in different scaled versions, classical SR methods such as [7], [16], [17] can be applied to synthesize the SR output. Although very promising SR examples were shown in [2], there is no guarantee that self-similarity always exists within or across image scales, and thus this prohibits the generalization of their SR framework for practical problems. Moreover, it is not clear what is the preferable magnification factor when applying their approach (SR images with different magnification factors were presented in [2]).

C. Sparse Representation for SR
Originally applied to signal recovery, sparse coding [18] has shown its success in image related applications such as image de-noising [19], and it was first applied to SR by Yang et al.[20], [21]. They considered the image patch from HR images as a sparse representation with respect to an over-complete dictionary composed of signal-atoms. They suggested that, under mild conditions, the sparse representation of high-resolution images can be recovered from the low-resolution image patches [20], [21]. They used a small set of randomly chosen image patches for training, and implied that their SR method only applies to images with similar statistical nature. Kim and Kwon [22], [23] proposed an example-based single image SR for learning the mapping function between the low and high-resolution images by using sparse regression and natural image priors. However, blurring and ringing effects near the edges exist in their SR results, and additional post-processing techniques are still needed to alleviate this problem. Recently, Yang et al. [24] extended the framework of [2]. Based on the assumption of image patch self-similarity, they concatenated high and low-resolution image pairs from the image pyramid and jointly learned their sparse representation. When super-resolve an LR input patch, they searched for similar patches from the image pyramid and use the associated sparse representation (the HR part) to predict its final SR version.

THE PROPOSED SELF-LEARNING APPROACH TO SINGLE IMAGE SUPER-RESOLUTION

1. Image patch Categorization
In a First step, the input image size is up-scaled into Magnitude factor. The up-scaling can be done by bi-cubic interpolation. To alleviate edge artifacts due to the bi-cubic interpolation, the input image is padded by four pixels on each side by replicating border pixels. The Image patch-based approach (developed at the same time as the texture-based prior presented here) for image-based rendering. For their application the likelihood function was multi-modal, and a prior was needed to help ensure consistency across the output image. For our application, a small image patch around each highresolution image pixel is selected. We can learn a distribution for this central pixel’s intensity value by examining the values at the centers of similar patches from other images.
The central pixel is held back, so that when a match is made between this neighbourhood vector and a new trial patch, the central pixel value can be returned as a prototype for what value we might expect to find associated with the centre of the new patch. The patches in the image are normalized to sum to unity, and centre weighted as in 2-dimensional Gaussian kernel. For simplicity, the patches are always chosen to be squares with an odd number of pixels to a side, and the Gaussian kernel standard deviations are chosen to be equal to the floor of half the width of the square, i.e. a 3×3 patch would use a Gaussian with a standard deviation of 3 pixels.

2. Sparse Representation
Sparse representations are representations that account for most or all information of a signal with a linear combination of a small number of elementary signals called atoms. Super-resolution as sparse representation in dictionary of raw image patches. The technique of finding a representation with a small number of significant coefficients is often referred to as Sparse Coding. Decoding merely requires the summation of the relevant atoms, appropriately weighted, however, unlike a transform coder with its invertible transform, the generation of the sparse representation with an overcomplete dictionary is non-trivial. The image patch self-similarity, they concatenated high and low-resolution image pairs from the image pyramid and jointly learned their sparse representation. The super-resolve an LR input patch, they searched for similar patches from the image pyramid and use the associated sparse representation (the HR part) to predict its final SR version.

3. Support Vector Regression
Support vector regression (SVR) is an extension of support vector machine, which is able to fit the data in a highdimensional feature space without assumptions of data distribution. Similar to SVM, the generalization ability makes the SVR very powerful in predicting unknown outputs, and the use of SVR has been shown to produce effective SR outputs. The observed SVR will be applied to predict the final SR output for a test LR input. our work in first synthesizes the HR version from the test input using bi-cubic interpolation. To refine this HR image into the final SR output, we derive the sparse representation of each patch and update the centered pixel value for each using the learned SVR models. While this refinement process exhibits impressive capability in producing SR images, its need to collect training LR/HR image data in advance is not desirable.

4. Kernel ridge regression of Optimization model
A parameterized combination functions and learns the parameters by solving an optimization problem. This optimization can be integrated to a kernel-based learner or formulated as a different mathematical model for obtaining only the combination parameters. In order to incorporate SVR with KRR (Kernel Ridge Regression), mixture probability should be formulated with SVR outputs Probabilistic output from SVR was done in phase I researches, but they didn’t consider optimization mixture probability. To find mixture probability with SVR in this research distance from Gradient, histograms and interpolation were used in this module.
A Gradient Pyramid approach is obtained by applying a set of 4 directional gradient filters (horizontal, vertical and 2 diagonal) to the Gaussian Pyramid at each level. At each level, these 4 directional Gradient Pyramids are combined together to obtain a combined gradient pyramid that is similar to a Laplacian pyramid. The gradient pyramid solution is therefore the same as the image angle using the Laplacian pyramid method except replacing the Laplacian pyramid with the combined Gradient Pyramid.
A good solution to suppress halos is to apply the scene gradients to adjust the gradient of the synthesized SDR image. The scene gradient information is adaptively captured by setting the different exposure levels, i.e., the scene gradients are captured through the local adaptation to the scene luminance for an window M × M centered at (x, y). Technically, the scene gradient of a point is reflected by the gradient that is perceivable by human eyes, called visible gradient, and that can be measured by counting the number of visible differences of luminance’s between neighboring pixels in the window.
To compute the quantity of the visible gradient ψ(x, y) by
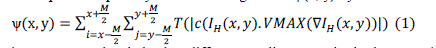image
These exposure levels lead to different gradient magnitudes because the gradient magnitude depends on the image luminances and the image luminance depends on the exposure level. The scene gradient extraction is a process to find gradient G(x, y) which maximizes the quantity of the visible gradient,
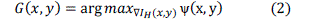image
In this gradient extraction, the pixels positions are estimated along with x-coordinate and y-coordinate. In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest increase rate in the scalar, and in the magnitude. The variation in space of any quantity can be represented (e.g. graphically) by a slope in general. The gradient represents the steepness and direction of the slope.

EXPERIMENTAL RESULTS
We first evaluate our proposed SR method with different magnification factors on several grayscale or color images. Besides presenting the SR images and their PSNR values, we also compare our results with those produced by state-of-the-art learning-based SR methods. We replace bicubic interpolation in our framework by other up-sampling or SR algorithms. This is to verify that our proposed framework is not limited to the use of any specific type of image upsampling techniques when constructing the image pyramids. These two parts of experiments are to verify the effectiveness and robustness of our proposed method, respectively.
Finally, we replace nearest neighbor interpolation by Gaussian blur kernels when down-sampling images in our experiments; this is to confirm that our method applies to practical image processing scenarios. More precisely, to synthesize the input LR images from their ground truth HR versions, we apply Gaussian blur kernels before down-sampling the images. The same down-sampling technique is also applied to construct the image pyramid in our proposed framework for self-learning purposes.

CONCLUSION
This paper proposed a novel in-scale self-learning framework for single image SR.We advanced the learning of multiple kernel learning for adaptive kernel selection and image sparse representation in our SR method, which exhibited excellent generalization in refining an up-sampled image into its SR version. Different from most prior learning-based approaches, our approach is very unique since we do not require training low and high-resolution image data.We do not assume context, edge, etc. priors when synthesizing SR images, nor do we expect reoccurrence of image patches in images as many prior learning-based methods did. Supported by the Bayes decision rule, our method produced excellent SR results on a variety of images, and we achieved a significant improvement in PSNR when comparing with state-of-the-art SR approaches. Moreover, by deploying different types of interpolation or SR techniques to up-sample images at intermediate scales in our framework, we confirmed the robustness and effectiveness of our proposed SR framework.

Tables at a glance
Table icon Table icon
Table 1 Table 2
 

Figures at a glance
Figure 1
Figure 1
 

References

  1. D. Glasner, S. Bagon, and M. Irani, “Super-resolution from a single image,” in Proc. IEEE Int. Conf. Comput. Vision, 2009.

  2. A. J. Smola and B. Schölkopf, A Tutorial on Support Vector Regression Statistics and Computing, 2003.

  3. M.-C. Yang, C.-T. Chu, and Y.-C. F. Wang, “Learning sparse image representation with support vector regression for single-image superresolution,”in Proc. IEEE Int. Conf. Image Processing, 2010.

  4. R. C. Hardie, K. J. Barnard, and E. E. Armstrong, “Joint map registration and high-resolution image estimation using a sequence of undersampledimages,” IEEE Trans. Image Process., vol. 6, no. 12, pp.1621–1633, 1997.

  5. N. Nguyen, P. Milanfar, andG. H. Golub, “A computationally efficient superresolution image reconstruction algorithm,” IEEE Trans. Image Process.,vol. 10, no. 4, pp. 573–583, Apr. 2001.

  6. S. Farsiu, D. Robinson, M. Elad, and P. Milanfar, “Fast and robust multi-frame super-resolution,” IEEE Trans. Image Process., vol. 13, no. 10, pp.1327–1344, Oct. 2004.

  7. S. Baker and T. Kanade, “Limits on super-resolution and how to break them,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 24, no. 9, pp. 1167–1183,Sep. 2002.

  8. J. Sun, J. Zhu, and M. F. Tappen, “Context-constrained hallucination for image super-resolution,” in Proc. IEEE Conf. Comput. Vision and PatternRecognition, 2010.

  9. M. E. Tipping and C. M. Bishop, “Bayesian image super-resolution,”Adv. Neural Inf. Processing Syst., 2002.

  10. H. Y. Shum and Z. C. Lin, “Fundamental limits of reconstruction-based superresolution algorithms under local translation,” IEEE Trans. PatternAnal. Mach. Intell., vol. 26, no. 1, pp. 83–97, Jan. 2004.

  11. A. Chakrabarti, A. N. Rajagopalan, and R. Chellappa, “Super-resolution of face images using kernel PCA-based prior,” IEEE Trans. Multimedia, vol.9, no. 4, pp. 888–892, 2007.

  12. M. Protter and M. Elad, “Image sequence denoising via sparse and redundant representations,” IEEE Trans. Image Process., vol. 18, no.1, pp. 27–35,Jan. 2009.

  13. W. T. Freeman, T. R. Jones, and E. C. Pasztor, “Example-based superresolution,” IEEE Comput. Graph. Appl., 2002.

  14. H. Chang, D.-Y. Yeung, and Y. Xiong, “Super-resolution through neighbor embedding,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognition, 2004.

  15. M. Irani and S. Peleg, “Improving resolution by image registration,” CVGIP: Graph. Models Image Process., vol. 53, no. 3, 1991.

  16. D. Capel, Image Mosaicing and Super-Resolution (Cphc/Bcs Distinguished Dissertations). New York, NY, USA: Springer-Verlag, 2004.

  17. D. L. Donoho, “Compressed sensing,” IEEE Trans. Inf. Theory, vol. 52, no. 4, pp. 1289–1306, 2006.

  18. J. Mairal, F. Bach, J. Ponce, G. Sapiro, and A. Zisserman, “Non-local sparse models for image restoration,” in Proc. ICCV, , pp. 2272–2279.

  19. J. Yang, J. Wright, T. S. Huang, and Y. Ma, “Image super-resolution as sparse representation of raw image patches,” in Proc. IEEE Conf. Comput.Vision and Pattern Recognition, 2008.

  20. J. Yang, J. Wright, T. Huang, and Y. Ma, “Image super-resolution via sparse representation,” IEEE Trans. Image Process., vol. 19, no. 11, pp. 2861–2873, Nov. 2010.

  21. K. I. Kim and Y. Kwon, Example-Based Learning for Single-Image Super-Resolution and jpeg Artifact Removal, Max-Planck-Institute for BiologicalCybernetics, Tübingen, Germany, 2008.

  22. K. I. Kim and Y. Kwon, “Single-image super-resolution using sparse regression and natural image prior,” IEEE Trans. Pattern Anal. Mach. Intell.,vol. 32, no. 6, pp. 1127–1133, Jun. 2010.

  23. C.-Y. Yang, J.-B. Huang, and M.-H. Yang, “Exploiting self-similarities for single frame super-resolution,” in Proc. Asian Conf. Comput. Vision, 2010, pp. 497–510.