Keywords
|
| Image registration, Feature extraction, Image blending, Image mosaicing, FAST, SIFT, SURF, PCA-SIFT. |
INTRODUCTION
|
| Image mosaicing is the stitching of multiple images correlated images to generate single large image with the seamless view. Image mosaicing consist of two basic concepts of image registration and image blending. |
| A. Image Registration |
| Image registration is the establishment of correspondence between the images of same scene. It is a process of aligning two images acquire by same or different sensors, at different time or from different viewpoint. To register images, we need to determine geometric transformation that aligns images with respect to the reference image [1]. |
| Steps involved in the registration process as in [2] are as follow: |
| 1) Feature Detection: Salient and distinctive objects in both reference and sensed images are detected. |
| 2) Feature Matching: The correspondence between the features in the reference and the sensed image established. |
| 3) Transform Model Estimation: The type and parameters of the so-called mapping functions, aligning the sensed image with the reference image, are estimated. |
| 4) Image Resampling: The sensed image is transformed by means of the mapping functions. |
| B. Image Blending |
| It is the final step to blend the pixels colours (or intensity) in the overlapped region to avoid the seams. Simplest available form is to use feathering, which uses weighted averaging colour values to blend the overlapping pixels. |
| Our main focus is on the first step of image registration process of feature detection. Features are the distinct elements in two images that are to be matched. The image mosaicing methods can be loosely classified based on the following classes as given in [3]. |
| ? Algorithms that uses pixel values directly, e.g., correlation methods. |
| ? Algorithms that uses frequency domain, e.g., Fast Fourier transform methods. |
| ? Algorithms that uses low level features like edges and corners detection. |
| ? Algorithms that uses high level features like identified parts of image objects, etc. |
RELATED WORK
|
| A literature review had been carried out for the feature based methods that are used in the process of image mosaicing. Different registration methods was explained by Manjusha Deshmukh and Udhav Bhosle in their survey paper [1]. Also the overview of such registration approaches was given in [2]. Hemlata Joshi and Khomlal Sinha given a survey of image mosaicing techniques with four different methods: Harris Corner, SIFT, FAST and SURF [3]. In paper [4], Annis Fathima, R. Karthik and V. Vaidehi proposed a method of image mosaicing method with SIFT and pre-processing step of finding overlapping region with moment calculation of images. A review of Image Mosaic based on feature technique was explained by Udaykumar B. Patel and Hardik N. Mewada, by using Harris Corner Detection method in [5]. A comprehensive study presented by Hetal M. Patel, Pinal J. Patel and Sandip G. Patel with Harris Corner, SIFT, SUSAN and Forstner Corner feature extraction methods with RANSAC algorithm to calculate homography [6]. Comparison of different feature extraction methods given in [7] by M. M. El-garar, H. Soliman and N. Meky. with five different algorithms. Feature extraction algorithm called SURF (scale and rotation invariant) proposed by Herbert Bay, Tinne Tuytelaars and Luc Van Gool in [8]. Variant of SURF algorithm which is also able to detect point with affine transformation, proposed by Yanwei Pang, Wei Li, Yaan Yuan and Jing Pan in [9]. A distinctive image features which are scale invariant (became SIFT) proposed by David G. Lowe in the paper [10]. PCA-SIFT was presented by Yan ke and Rahul Sukthankar in [11]. A technique of image mosaicing was given with simplified version of SIFT by Li Jin, Wang Yanwei and Liang Hong [12]. Survey of different registration methods was explained in [13] by Barbara Zitova and Jan Flusser. |
FEATURE EXTRACTION TECHNIQUES
|
| Using the image features obtained from the corresponding images taken from different viewpoints, image stitching is achieved. Block matching and feature-point matching are the two basic ways to identify the matching region from the input images. Block matching algorithms calculate the correlation between regular-sized blocks generated in sequential images. Such methods include either Normalized Cross-Correlation or phase correlation using an Fast Fourier Transform. Such methods involve a series of complex calculation and also very sensitive to the slight distinction between images. Feature based methods extract distinctive features from each image and matches these features to establish a global correspondence [4]. |
| A. Harris Corner Detection |
| Harris corner detector is a well-known interest key point detector due to its invariance to rotation, illuminations variation and image noise which has been proposed in 1988. Harris corner are not scale-invariant. It is based on local auto-correlation function of a signal where local auto-correlation function measures the local changes of the signal with patches shifted by a small amount in different directions. Harris promotes a formula that can be calculated out the change of the pixel values in any direction, rather than fixed in the 8 directions [5]. Let the grey of pixel (x, y) be g(x, y), then the grey variation of pixel (x, y) with a shift (p, q) can be described as (1). |
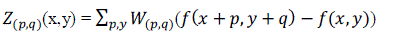 (1) (1) |
| In equation (1), the gray variation can be define using differential operation |
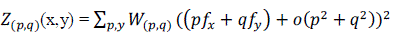 (2) (2) |
| is the first-order gray gradient u, v is Gaussian operator |
| Calculate the auto-correlation matrix |
| To extract the corner, Harris constructed the formula as below |
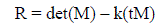 (3) (3) |
| det(M) is the determinant of M and tM is the trace of M, where k is the parameter greater than zero. The feature points that are the pixel value corresponding with the local maximum interest point, are taken into consideration with Harris method [5]. |
| B. SUSAN |
| Smallest Univalue Segment Assimilating Nucleus (SUSAN) places a circular mask or called window over the pixel to be tested. The region of the mask is M. pixel in mask is represented by m. The nucleus is at ??. The brightness of pixel with in mask is compared with that of the nucleus [6]. Every pixel is compared to the nucleus using following function: |
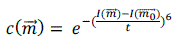 (4) (4) |
| here t represent radius, power of exponent is determined empirically. The area of SUSAN is given by, |
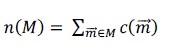 (5) (5) |
| If c is rectangular function, then n is the number of pixels in the mask which are within ? of the nucleus [6]. The response of the SUSAN operator is given by |
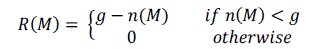 (6) (6) |
| Then after, first, the centroid of the SUSAN is found. A proper corner will have the centroid far from the nucleus. The second is that all points on the line from the nucleus through the centroid out to the edge of the mask are in the SUSAN [6]. |
| C. FAST |
| Trajkovic and Hedley presented a corner detector algorithm in 1998 known as FAST. It is based on SUSAN corner criterion. The detection of corner was prioritized over edges in FAST as corners were found to be the good features to be matched because it shows a two dimensional intensity change, and thus well distinguished from the neighbouring points. According to Trajkovic and Hedley the corner detector should satisfy the following criteria [3], [7]. |
| 1) The detected positions should be consistent, insensitive to the variation of noise, and they should not move when multiple images are acquired of the same scene. |
| 2) Accuracy: Corners should be detected as close as possible to the correct positions. |
| 3) Speed: The corner detector should be fast enough. |
| FAST incremented the computational speed required in the detection of corners. This corner detector uses a corner response function (CRF) that gives a numerical value for the corner strength based on the image intensities in the local neighborhood.CRF was computed over the image and corners which were treated as local maxima of the CRF.A multigrid technique is used to improve the computational speed of the algorithm and also for the suppression of false corners being detected. FAST is an accurate and fast algorithm that yields good localization (positional accuracy) and high point reliability [3]. |
| D. SURF |
| A basic second order Hessian matrix approximation is used for feature point detection. The approximation with box filters is pushed to take place of second-order Gaussian filter. And a very low computational cost is obtained by using integral images. The Hessian-matrix approximation lends itself to the use of integral images, which is a very useful technique. Hence, computation time is reduced drastically [8], [9]. |
| In the construction of scale image pyramid in SURF algorithm, the scale space is divided into octaves, and there are 4 scale levels in each octave. Each octave represents a series of filter response maps obtained by convolving the same in put image with a filter of increasing size. And the minimum scale difference between subsequent scales depends on the length of the positive or negative lobes of the partial second order derivative in the direction of derivation. Do nonmaximum suppression in a 3x3x3 neighbourhood to get the steady feature points and the scale of values. |
| In order to be invariant to image rotation, the Haar wavelet responses are calculated in x and y direction within a circular neighbourhood of radius 6s around the feature point, s is the scale at which the feature point was detected. The Haar wavelet responses are represented as vectors. Then sum all the vector of x and y direction of the Haar wavelet responses within a sliding orientation window covering an angle of size π/3 around the feature point. The two summed response yield a new vector. And the longest vector is the dominant orientation of the feature point. |
| For extraction of the descriptor, construct a square region with a size of 20s and split the interest region up into 4x4 square sub-regions with 5x5 regularly spaced sample points inside. Compute the Haar wavelet response x-direction and the Haar wavelet response y-direction . Weight the response with a Gaussian kernel centered at the interest point. Sum the response over each sub-region for and separately. In order to bring in information about the polarity of the intensity changes, extract the sum of absolute value of the responses. Therefore, each sub-region is formed a 4-dimensional vector, |
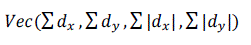 (7) (7) |
| Finally, normalize the vector into unit length for invariance to contrast [8], [9]. |
| E. SIFT |
| Scale Invariant Feature Transform (SIFT) consists of four stages as below: |
| 1) Scale-space extrema detection: The first stage of computation searches over all scales and image locations. It is implemented efficiently by using a difference-of-Gaussian function to identify potential interest points that are invariant to scale and orientation. |
| 2) Keypoint localization: At each candidate location, a detailed model is fit to determine location and scale. Keypoints are selected based on measures of their stability. |
| 3) Orientation assignment: One or more orientations are assigned to each keypoint location based on local image gradient directions. All future operations are performed on image data that has been transformed relative to the assigned orientation, scale, and location for each feature, thereby providing invariance to these transformations. |
| 4) Keypoint descriptor: The local image gradients are measured at the selected scale in the region around each keypoint. These are transformed into a representation that allows for significant levels of local shape distortion and change in illumination. |
| The first stage used difference-of-Gaussian (DOG) function to identify potential interest points, which were invariant to scale and orientation. DOG was used instead of Gaussian to improve the computation speed. |
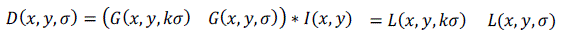 (8) (8) |
| Where * is the convolution operator, G(x, y, ??) is a variable scale Gaussian, I(x, y) is the input image D(x, y, ??) is Difference of Gaussians with scale k times. In the keypoint localization step, they are rejected the low contrast points and eliminated the edge response. Hessian matrix was used to compute the principal curvatures and eliminate the keypoints that have a ratio between the principal curvatures greater than the ratio. An orientation histogram was formed from the gradient orientations of sample points within a region around the keypoint in order to get an orientation assignment. According to experiments, the best results were achieved with a 4x4 array of histograms with 8 orientation bins in each. So the descriptor of SIFT that was used is 4x4x8= 128 dimensions [7], [10], [12]. |
| F. PCA-SIFT |
| Principal Component Analysis (PCA) is a standard technique for dimensionality reduction and has been applied to a broad class of computer vision problems, including feature selection. PCA-SIFT can be summarized in the following steps [11]: |
| 1) Pre-compute an eigenspace to express the gradient images of local patches |
| 2) Given a patch, compute its local image gradient |
| 3) Project the gradient image vector using the eigenspace to derive a compact feature vector |
| The input vector is created by concatenating the horizontal and vertical gradient maps for the 41x41 patch centered at the keypoint. Thus, the input vector has 2x39x39=3042 elements. Then normalize this vector to unit magnitude to minimize the impact of variations in illumination. Projecting the gradient patch onto the low-dimensional space appears to retain the identity related variation while discarding the distortions induced by other effects. |
| Eigenspace can be build by running the first three stages of the SIFT algorithm on a diverse collection of images and collected 21,000 patches. Each was processed as described above to create a 3042-element vector, and PCA was applied to the covariance matrix of these vectors. The matrix consisting of the top n eigenvectors was stored on disk and used as the projection matrix for PCA-SIFT. The images used in building the eigenspace were discarded and not used in any of the matching experiments [11]. |
CONCLUSION
|
| In this paper, we have discussed some commonly used methods of features extraction for image mosaicing application. Harris Corner detection algorithm is rotational invariant and can perform well in the absence of scale difference. SUSAN is also a corner detection technique with a mask that calculates the intensity differences to find the corners, but this method is not scale invariant. A rotation and scale invariant algorithm called FAST has improved execution time in absence of noise. SIFT, SURF and PCA-SIFT are descriptor based algorithms and have advantages over different conditions. SIFT is invariant to rotation, illumination and affine transformation changes, and shows good performance in most of the cases but has slow execution time. SURF is superior with execution time. PCA-SIFT reduced the execution time of SIFT matching but was proved to less effective than SIFT in extracting the feature points. |
ACKNOWLEDGMENT
|
| I am very grateful and would like to thank my guides Prof. Mahasweta Joshi and Prof. Vikram Agrawal for their advice and continued support. Without them, it would have not been possible for me to complete this paper. I would like to thank all my friends for the thoughtful and mind stimulating discussion we had, which prompted us to think beyond the obvious. |
References
|
- ManjushaDeshmukh, UdhavBhosle, “A Survey of Image Registration”, International Journal of Image Processing (IJIP), Volume (5) : Issue (3) ,2011.
- Medha V. Wyawahare, Dr. Pradeep M. Patil, and Hemant K. Abhyankar, “Image Registration Techniques: An overview”, International Journal ofSignal Processing, Image Processing and Pattern Recognition, Vol. 2, No.3, September 2009.
- Hemlata Joshi, Mr. KhomlalSinha, “A Survey on Image Mosaicing Techniques”, International Journal of Advanced Research in ComputerEngineering & Technology (IJARCET) Volume 2, Issue 2, February 2013.
- .AnnisFathima, R. Karthik, V. Vaidehi, “Image Stitching with Combined Moment Invariants and SIFT Features”, Procedia Computer Science19 ( 2013 ) 420 – 427.
- Udaykumar B Patel, Hardik N Mewada, “Review of Image Mosaic Based on Feature Technique”,International Journal of Engineering andInnovative Technology (IJEIT) Volume 2, Issue 11, May 2013.
- Hetal M. Patel, Pinal J. Patel, Sandip G. Patel, “Comprehensive Study And Review Of Image Mosaicing Methods”, International Journal ofEngineering Research & Technology (IJERT), Vol. 1, Issue 9, November- 2012.
- M.M. El-gayar, H. Soliman, N. meky, “A comparative study of image low level feature extraction algorithms”, Egyptian Informatics Journal(2013) 14, 175–181.
- Herbert Bay, TinneTuytelaars, and Luc Van Gool, “SURF: Speeded Up Robust Features”, ETH Zurich, KatholiekeUniversiteit Leuven.
- Yanwei Pang, Wei Li, Yuan Yuan, Jing Pan, “Fully affine invariant SURF for image matching”, Neurocomputing 85(2012)6–10.
- David G. Lowe, “Distinctive Image Features from Scale-Invariant Keypoints”, Computer Science Department, University of British Columbia,Vancouver, B.C., Canada. (Accepted for publication in the International Journal of Computer Vision, 2004).
- Yan Ke, Rahul Sukthankar, “PCA-SIFT: A More Distinctive Representation for Local Image Descriptors”, School of Computer Science,Carnegie Mellon University, Intel Research Pittsburgh.
- Li Jin ,WangYanwei ,Liang Hong, “Image Mosaic Based on Simplified SIFT”, 2012 International Conference on Mechanical Engineering andAutomation Advances in Biomedical Engineering, Vol.10.
- Barbara Zitova, Jan Flusser, “Image registration methods: a survey”, Image and Vision Computing 21 (2003) 977–1000.
|