Keywords |
| Genetic algorithm (GA), peak to average power ratio (PAPR), Selected mapping scheme (SLM),
Nonlinear compounding Techniques (NCT) |
INTRODUCTION |
| Around 1805, Carl Friedrich Gauss invented a revolutionary technique for efficiently computing the coefficients of
what is now called discrete Fourier series. Unfortunately, Gauss never published his work and it was lost for over one
hundred years. During the rest of the nineteenth century, variations of the technique were independently discovered
several more times, but never appreciated. In the early twentieth century, Carl Runge derived an algorithm similar to
that of Gauss that could compute the coefficients on an input with size equal to a power of two and was later
generalized to powers of three. |
| Over 2,000 additional papers have been published, and the Fast Fourier Transform (FFT) has become one of the
most important techniques in the field of Electrical Engineering. The revolution had finally started; Charles Fiducia
showed for the first time that the FFT can be computed in terms of algebraic modular reductions. As with the early FFT
publications, this idea has been generally ignored. However, Daniel Bernstein recently wrote several unpublished
works, which expand upon the observations of Fiducia and show the algebraic transformations involved in this
approach to computing the FFT. |
| Several applications of the FFT that can be improved using the new algorithms including polynomial division, the
computation of the greatest common divisor, and decoding Reed-Solomon codes. Another motivation for writing this is
to provide a treatment of the FFT that takes the perspective of both mathematicians and engineers into account so that
these two communities may better communicate with each other. The engineering perspective of the FFT has been
briefly introduced in these opening remarks. Now consider the mathematician’s perspective of the FFT. |
| 1. PAPR in OFDM |
| One of the main disadvantages of the OFDM systems is the high PAPR of the transmitted signal due to the
combination of N modulated SCs. |
PAPR REDUCTION TECHNIQUES |
| This paper introduces the main PAPR reduction techniques in OFDM systems. Several conventional
techniques for PAPR reduction in the OFDM systems are investigated. Moreover, the criteria for selecting the
reduction technique that can reduce the PAPR effectively and simultaneously maintain the high-quality performance
are studied. Finally, it presents the literature review of the recent research scenarios in PAPR reduction based on the
PTS and SLM scheme. |
| 2. Significant PAPR Reduction Schemes |
| Various techniques have been proposed to reduce the PAPR comprising amplitude clipping, clipping and
filtering , coding schemes , phase optimization, NCT , TR and TI , active constellation extension ACE , multiple signal
representation techniques such as PTS and SLM and interleaving. |
| Clipping and filtering |
| The most straightforward and widely used technique of PAPR reduction is amplitude clipping. This technique
can be implemented by either clipping parts of the signals that are greater than a threshold level or by transmitting the
input signal below the threshold level without clipping. In the clipping technique, the BER performance of the OFDM
systems is deteriorated due to the in-band distortion, while the spectral efficiency is degraded owing to the out-of-band
radiation. The out-of-band radiation can be decreased by filtering the signal after clipping it. |
| In this technique, the input data block d, which consists of N symbols, is partitioned into V disjoint sets d (v),
v = 0, 1, V −1 and zero padded left and right to obtain |
| Selected mapping scheme |
| The block diagram of the conventional SLM (CSLM) scheme is shown in Fig. 3.4 [40]. The data symbols are copied
into U sections, each multiplied by U different phase sequences a (u) = [ a(u)0 , a(u) 1 , · · · , a(u) N−1] with u = 0, 1, · |
| Nonlinear companding transforms |
| One of the interesting PAPR reduction approaches are NCT. These transforms have two main advantages in
addition to high capability to the PAPR reduction: low implementation complexity and no bandwidth expansion. |
| Tone reservation and tone injection schemes |
| TR and TI are two well-known schemes to reduce the PAPR of OFDM systems. The OFDM signal peaks can
be reduced by inserting a subset of tone-dependent time-domain signals to the original OFDM signal. The time-domain
signal can be calculated easily using different algorithms at the transmitter and discarded at the receiver. Note that the
inserted signals have no effect on the data carrying SCs as the SCs are orthogonal in the OFDM systems. The
transmitter of the TR scheme sends data on a large subset of SCs to minimize the PAPR reduction. |
FACTORS FOR SELECTING THE PAPR REDUCTION TECHNIQUE |
| Several factors should be considered for selecting the technique that can reduce the PAPR effectively while
simultaneously maintaining the high-quality performance. |
| These factors are as follows |
| 1. High capability PAPR reduction: clearly, this is the major factor to be taken into account for selecting the PAPR
reduction method. In particular methods such as the amplitude clipping and NCT, the destructive effects of the in-band
distortion and out-of-band radiation should be considered. |
| 2. Low average power in transmit signal: the average power of the transmit signals is increased after utilising some
PAPR reduction methods such as TR and TI. The average power must be normalised after the PAPR reduction to the
power level before the PAPR reduction. This normalisation causes degradation in the BER performance |
| 3. No BER performance degradation at the receiver: the main idea of the PAPR reduction in OFDM signals is to
achieve an improvement in the BER performance. This performance degrades due to the in-band distortion in clipping and NCT schemes. Furthermore, recovering the side information incorrectly at the receiver side in the PTS and SLM
schemes is another cause of BER performance degradation. |
| 4. No loss in data rate: in consequence of sending the SI, the signal bandwidth expands in a few schemes such as PTS,
SLM and coding. The data rate will reduce due to the bandwidth expansion. To perform the original data rate of the
OFDM signal, the SI should be embedded. |
| 5. Low computational complexity: commonly, more complex schemes can achieve superior PAPR reduction. However,
a scheme such as PTS reduces the PAPR by exhaustive searching of weighing phase factors. Therefore, the desired
time and hardware for the PAPR reduction should be reduced to the minimum possible. |
| 6. No spectral spillage: OFDM is immune to the multipath fading consequently |
| 3.Genetic algorithm for PAPR reduction of OFDM signal |
| Choose an initial population of chromosomes; |
| While termination condition not satisfied do |
| Repeat |
| If crossover condition satisfied then
{select parent chromosomes;
Choose crossover parameters;
Perform crossover};
If mutation condition satisfied then
{choose mutation points;
Perform mutation};
Evaluate fitness of offspring
Until sufficient offspring created;
Select new population;
End while |
| Crossover |
| Crossover is simply a matter of replacing some of the genes in one parent by the corresponding genes of the
other. Suppose we have two strings a andb, each consisting of 6 variables, i.e. which represent two possible solutions to
a problem. (Note that we have chosen here to leave the alphabet unspecified, to emphasize that binary representation is
not acritical aspect of GAs.) One-point crossover (1X) has been described earlier; two-point crossover (denoted by 2X),
is very similar. Two cross points are chosen at random from the numbers and a new solution produced by combining
the pieces of the original ‘parents’. |
| Mutation |
| In the case when crossover-OR-mutation is used, we must first decide whether any mutation is carried out at
all. Assuming that it is, the concept of mutation is even simpler than crossover, and again, this can easily be represented
as a bit-string. |
RESULT AND DISCUSSION |
| SIMULATED OUTPUT |
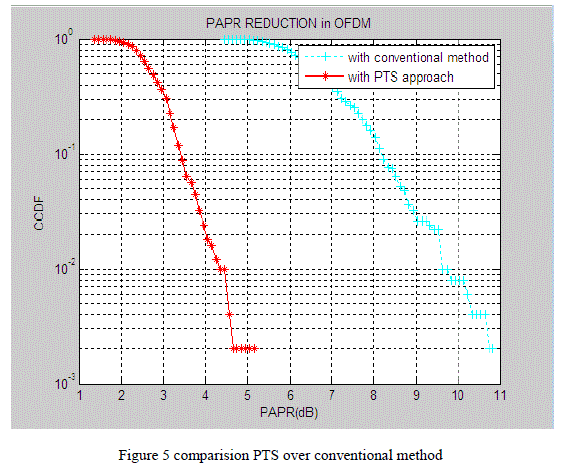
| COMPARISION PTS OVER CONVENTIONAL METHOD: |
| PERFORMANCE REPORT: |
CONCLUSIONS AND FUTURE WORK |
| In our paper we perused the concept of covered the basic principles of GAs, the number of variations that have
been suggested is enormous. Many variations in population size, in initialization methods, in fitness definition, in
selection and replacement strategies, in crossover and mutation are obviously possible. We can add information such as
age, or artificial tags, to chromosomes; in order to reduce complexity further. |
Figures at a glance |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
 |
 |
 |
| Figure 4 |
Figure 5 |
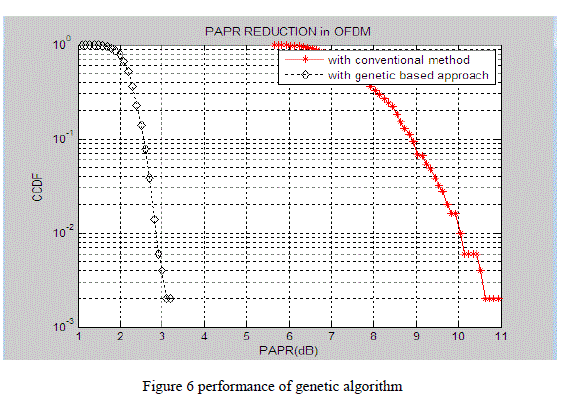
Figure 6 |
|
| |
References |
- Bergland, Glenn D. A Radix-Eight Fast Fourier Transform Subroutine for Real-Valued Series. IEEE Transactions on audio and electroacoustics,17(2):138-44, 1969.
- Bernstein, D. Multidigit Multiplication for mathematicians. Preprint. Available at: <http://cr.yp.to/papers.html\#m3>.
- Bernstein, D. Fast Multiplication and its applications. Preprint. Available at: <http://cr.yp.to/papers.html\#multapps>.
- Bernstein, D. The Tangent FFT.Preprint. Available at: <http://cr.yp.to/papers.html\#tangentfft>.
- Bittinger, Marvin L. Intermediate Algebra, 9th Edition, Pearson Education(2003).
- Bouguezel, Saad, M. Omair Ahmad, and M.N.S. Swamy. An Improved Radix- 16 FFT Algorithm, Canadian Conference on Electrical andComputer Engineering, 2: 1089-92, 2004.
- Bouguezel, Saad, M. Omair Ahmad, and M.N.S. Swamy. Arithmetic Complexity of the Split-Radix FFT Algorithms, International ConferenceonAcoustics, Speech, and Signal Processing, 5: 137-40, 2005.
- Brent, Richard P., Fred G. Gustavson, and David Y. Y. Yun. Fast Solution of Toeplitz Systems of Equations and Computation ofPadeApproximants.Journal of Algorithms, 1: 259-295, 1980.
- Brigham, E. Oran. The Fast Fourier Transform and its Applications, PrenticeHall (1988).
- ]Buneman, Oscar. Inversion of the Helmholtz (or Laplace-Poisson) Operator for Slab Geometry, Journal of Computational Physics, 12: 124-30,1973.
- Burden, Richard L. and J. Douglas Faires. Numerical Analysis, Fifth Edition, PWS Publishing Company (1993).
- Cantor, David G. On arithmetical algorithms over finite fields, J. Combinatorial Theory, Series A, 50(2): 285-300, 1989.
- Cantor, David G. and Erich Kaltofen. On fast multiplication of polynomials over arbitrary algebras, ActaInformatica, 28: 693-701, 1991.
- Chu, Eleanor and Alan George. Inside the FFT Black Box: Serial and Parallel Fast Fourier Transform Algorithms, CRC Press (2000).
- Conway, John. The Book of Numbers, Springer (1996).
- Cooley, J. and J. Tukey. An algorithm for the machine calculation of complex Fourier series, Mathematics of Computation, 19: 297-301, 1965.
- Cormen, Thomas H., Charles E. Leiserson, and Ronald L. Rivest. Introduction to Algorithms, MIT Press (1997).
- Crandall, Richard and Barry Fagin. Discrete weighted transforms and largeinteger arithmetic, Mathematics of Computation, 62: 325-324, 1994.
- Ding, C., D. Pei, and A. Salomaa. Chinese Remainder Theorem: Applications in Computing, Coding, Cryptography, World Scientific (1996).
- Dubois, Eric and Anastasias N. Venetsanopoulos. A New Algorithm for the Radix- 3 FFT, IEEE Transactions on Acoustics, Speech, and SignalProcessing, 26(3): 222-5, 1978.
- Duhamel, Pierre and H. Hollmann. Split-radix FFT algorithm, Electronic Letters, 20: 14-6, 1984.
- Duhamel, P. and M. Vetterli. Fast Fourier Transforms: A tutorial review and a state of the art, Signal Processing, 19: 259-99, 1990.
|