ISSN:2321-6212
ISSN:2321-6212
Iqbal R1, Hayat SS1,2*, Ahmad S1
1Department of Physics, Hazara University, Pakistan
2Department of Physics, The Islamia University of Bahawalpur, Pakistan
Received date: 10/01/2016; Accepted date: 29/02/2016; Published date: 03/03/2016
Visit for more related articles at Research & Reviews: Journal of Material Sciences
The linearized augmented plane wave (LAPW) method within the generalized gradient approximation (GGA) based on the density functional theory (DFT) is used to investigate the properties of fluorite structure actinide oxides such as AmO2 and PuO2. This work presents the study of the behavior of 5f sates and the fully relativistic spin-orbit coupling of the actinide compounds. The value of the Fermi energy for the AmO2 and PuO2 materials is 0.80561 and 0.78551 eV, respectively. The spin dependent structures show that the energy crosses the Fermi level which shows the both materials are metallic in nature. The crystal field splitting shows the energy gap for eg and t2g states. The value of crystal field splitting is 3.2 and 4.6 eV for AmO2 and PuO2, respectively.
Actinides; Nuclear compounds; AmO2 and PuO2; Structural and magnetic materials
The Minor Actinides (such as Np, Am and Cm) accumulated in the nuclear reactor are considered as the most important part of the long-life radioactive waste. Their burning in the new generation nuclear reactors is proposed to reduce the required volume for the waste definitive proposal [1]. Actinide based materials possess interesting physical behavior due to the existence of 5f electrons and have attracted extensive attentions [2-8]. Observation of a high energy peak in the inelastic neutron scattering cross section is a clear indication of the localized nature of the 5f states [9]. The corrosion behavior of nuclear materials has been often unusual and difficult to interpret because of the complex electronic structure of the actinide elements and their radioactivity. Plutonium (Pu) element is a reactive metal whose surface does easily oxidize to Plutonium dioxide (PuO2) when exposed to air and moisture [10]. PuO2 is a chemically stable Pu oxide, which shows no sign of reaction when exposed to air [11]. Chemical properties of the actinide compounds are not characterized by only 5f electrons but also by 6d or 7s electrons, so that it is very complicated to clarify their behavior. Therefore, understanding of the valence state of Americium (Am) in the oxide nuclear fuel is one of the key issues for the management of oxide nuclear fuels. To evaluate the behavior of Am in the oxide nuclear fuel, the local and electronic structures around Am atom provide indispensable information, because the valence state of Am strongly affects the chemical potential of oxygen and thermal properties of the fuels [12,13].
Different physical properties of (AmO2) have been investigated in experiments ever since 1969 [13,14]. Americium has high and lasting radio toxicity that can cause problems especially in view of the long term safety issues for the final disposal of radioactive waste. It is, therefore, better to recycle Am into a reactor and to transmute it into stable or less-toxic nuclides. Thus, Am-containing oxides are considered as promising transmutation devices [15,16]. Among the MAs, Americium presents a major concern because of the extremely high oxygen potentials of Am-containing oxides [17-21]. Their oxygen potentials are indispensable data for safe irradiation in a reactor. Among them, (Pu, Am)O2–X is a candidate form for the Am-containing oxide for both fast reactors [17] and accelerator driven sub-critical systems [22]. Therefore, it is important to evaluate the properties of the MA oxides. However, there is only a little information on the properties for the MA oxides; in addition they are limited to a few properties, or a small temperature range. This is because of the difficulties associated with the high radiation fields. Since, the recycled fuel will be widely used in the future, it is necessary to develop a new technique to evaluate the thermophysical properties of the MA oxides, Recently, minor actinides (MAs), especially Am, have become of special concern for the establishment of a future nuclear fuel cycle that is compatible with the requirements for a reduced environmental burden and sustainable energy supply [23]. To reduce the potential long-term hazard of radioactive wastes, transmutation of MAs is considered to be an important option for the future nuclear fuel cycle [24]. Within the framework of the studies on nuclear waste transmutation, it is important to study the chemical thermodynamic properties (among others) of the minor actinide (MA) compounds. The minor actinide oxides as composites with MgO or solid solutions with UO2 or stabilized ZrO2 are considered as fuels for transmutation [25]. Therefore, the local and electronic structures around the Am atom in the oxide fuels are providing indispensable information because the valence state of Am strongly affects the oxygen potentials and thermal properties of the MA-MOX fuels [24].
In this study we do concentrate on the fundamental properties linked with different states s, p, d and f, but our main focus is on the 5f electrons. Actinide materials have been extensively studied due to their interesting physical behaviors of the 5f states and always attracted particular attention because of their importance in nuclear fuel cycles [26-29]. Plutonium mixed oxides (MOX) have several isotopes with different decay constants. In present work the lattice constants, electronic, Bulk moduli, band structures, total and partial density of states of actinide oxides are calculated using the linearized augmented plane wave (LAPW).
In order to investigate the structural and electronic properties of PuO2 and AmO2 at ground state, we do perform the First principle simulations which have been carried out using the WIEN2k code [30,31]. In this work, full potential linearized augmented plane wave (FP-LAPW) method [32] within the generalized gradient approximation (GGA) [33] are used to solve the Kohn-Sham equations, to estimate the structural, electronic and magnetic properties of PuO2, AmO2. The linearized augmented plane waves (LAPW) and augmented plane wave with local orbitals (APW + lo) are adopted as basis because the highest efficiency is found for a mixed basis set. Plutonium (6s2 7s2 6p6 6d2 5f6), Americium (6s2 7s2 6p6 6d2 5f7), Uranium (6s2 7s2 6p6 6d15f3) and Oxygen (2s2 2p4) are dealing with valence states. For the quantum mechanical understanding, the Density Functional Theory [34,35] calculations have been performed by employing the local density approximation (LDA) [36] to describe the electron exchange and correlation or the generalized gradient approximation [37] (GGA) for the exchange-correlation functional. Semi-core states are included so that more accurate results can be achieved.
For the exchange-correlation potential we used the form derived by Perdew et al. [38]. Basis functions are expanded simultaneously as spherical harmonic functions (inside non-overlapping muffin-tin (MT) spheres centred at atomic sites) and as plane waves in the interstitial region. The ι-expansion (azimuthal quantum number) of the non-spherical potential and charge density inside MT spheres is carried out up to l ιmax = 10. The plane waves are expanded up to a cut-off parameter, kmax, fulfilling the relation RMT kmax = 8, where RMT is the average radius of MT spheres
The electronic properties of crystalline AmO2 and PuO2 materials are investigated by using the spin polarized electronic band structures with GGA method. The calculated band structures of AmO2 and PuO2 materials are presented in the Figures 1a-2b. It is clear from the Figure 1a that there exists the band gap of 3.2 eV for the spin up of AmO2. It is clearly seen that the Fermi level crosses the valence band. This crossover shows that AmO2 material is metallic in nature. For PuO2, it is clear from the Figure 2a that Fermi level also crosses the valence band and there exists a band gap of 2.8 eV above the Fermi level and this shows that the PuO2 material is also metallic in nature. Figures 1b and 2b have the calculated band structures for the spin down states of AmO2 and PuO2, respectively. These figures show that there exist the band gaps of 1.6 and 0.01 eV for the spin down for AmO2 and PuO2, respectively. These figures show that the Fermi level crosses the valence band. These crossovers show that these materials are metallic in nature in case of both spins.
This theoretical investigation of PuO2 and AmO2 materials shows that the difference in lattice constant can be seen clearly in their band gaps for the both materials. The band gap for the majority spin can be seen 3.2 and 2.8 eV for PuO2 and AmO2, respectively. The value of difference in majority spins for these materials is 0.4 eV. In case of minority spin the band gap is 1.6 and 1.0 eV for PuO2 and AmO2, respectively. Difference of band gap of PuO2 and AmO2 is 0.6 eV for the minority spin. The 5f electronic states of these actinides in AmO2 and PuO2 materials have the largest overlap due to contribution of oxygen-2p states. However, these values are different from the other works on PuO2 [39-44].
The calculated spin polarized total density of states for PuO2 and AmO2 are shown in the Figure 3a and 3b, respectively. For PuO2, it is clear from the figure that the states in the energy range -7.41 to -2.5 eV are due to the incomplete O-p state with a small contribution of the Pu-6d state. Therefore, it is sure that this region has majority contribution of O-p state. The obtained electronic states show metallic character with considerable 5f state disturbing at the Fermi energy with 6 electrons in f state. There is an energy shift lies between the range: 1.25 to 2.8 eV. It can be observed an energy shift that occurs in the conduction band which is due to the contribution of p-state of the oxygen in the above mentioned range. The repulsion can be observed in the range: 2.9 to 9.8 eV for the both O and Pu atoms. For AmO2 similar pattern can be seen in the range: -7.41 to -2.5 eV. The majority contribution in this region is due to the O-p state and minority contribution is due to 6-d state. Therefore, metallic behavior of AmO2 material can be observed in this region because of 5f states disturbing at the Fermi energy with the contribution of 7 electrons in f-state. The similar pattern can be seen for PuO2 which is due to the presence of 6-d states. The only change in their peaks of f states is due to the difference of electrons in f-states of PuO2 and AmO2 materials.
Figure 4 carries the comparison of the f-sates for both materials. It is clear from the graph that the dominant peak is of the Am atom in the region of -0.8 to -0.65 eV. The decrease can be observed from valence band to the conduction band and a phase shift is clearly observed in the conduction band. There is a small distortion found when phase shift occurs for both materials. In case of Pu the peak of the f-state shifted towards the Fermi level and interested factor is observed when it does shifts to spin down. A narrow gap of 0.6 eV for Pu and 0.15 eV for Am is found when it does the phase shift.
Figure 5 shows that there is an overlapping for Am-d and Am-p states of the oxygen in the region of -7.5 to -2.5 eV and repulsion can also be seen in this region for all states. But the interesting result can be seen in the region of -1 to 2.6 eV. There is a sudden change in the energy before the Fermi energy and it goes to decrease. A shift can be found from one spin to another in the above said region and same shift can be observed in Figure 4.
Figure 6 shows that there is an overlapping for Pu-p and Pu-d states in the range of -7.5 to -2.5 eV and repulsion can also be observed in this region for all states. Interesting result is seen in the region -1.0 to 2.6 eV. There is a sudden change in the energy before the Fermi energy and it tends to decrease. In this region a shift can be found from one spin to another spin.
The interesting feature of these materials is the crystal field splitting which describes two sets of degeneracy. These two states are doubly degenerate ‘eg’ state and triply degenerate ‘t2g’ state as shown in Figures 7 and 8, respectively. The three lower-energy orbitals (dxy, dxz and dyz) are collectively referred to as t2g state and the two higher-energy orbitals (dz2 and dx2-y2) as eg state. The total density of states is projected onto atomic d orbitals. The bandwidth of the AmO2 for eg state is 3.5 eV and for t2g state is 1.9 eV with centered at 5.25 and 8.45 eV, respectively. The difference between these two centers is 3.2 eV which is the crystal field splitting for AmO2 material. The bandwidth of the PuO2 for eg state is 3.4 eV and for t2g state is 4.7 eV with centered at 4.7 and 8.16 eV, respectively. The difference between these two centers is 3.46 eV, which is the crystal field splitting for PuO2 material.The calculated lattice constant in this study for AmO2 and PuO2 are 5.3263 and 5.305 Å, respectively. The experimental lattice constants are 5.380 and 3.5401 Å for AmO2 and PuO2, respectively. These calculated values are 1% less for AmO2 and 1.778 % less for PuO2 as compared to the experimental values [45,46]. This shows that a comparable result is obtained. The results of these calculations clearly shows that the metallic 5f states have been found, in other words the metallic 5f states might affect the surface chemistry either with hybridization or transfer change from/to electronic states (Table 1).
| Compounds | Calculations | Lattice Constant (Å) | Bulk Modulus (GPa) | Band Gaps (eV) |
|---|---|---|---|---|
| AmO2 | This work | 5.3263 | 225.9977 | 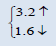 |
| Other Calculations | 5.380* | |||
| PuO2 | This work | 5.305 | 220.5339 | 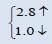 |
| Other calculations | 5.3901** |
Table 1: Calculated values of lattice constants, bulk moduli, and bandgap energies for AmO2 and PuO2[45-46]
We concluded that the Fermi energy of the AmO2 and PuO2 materials are 0.80561 and 0.78551 eV, respectively. The spin dependent structures show that the energy crosses the Fermi level which shows the both actinide oxides are metallic in nature. In case of AmO2 material, the peak of the density of states (DOS) is higher and away from the Fermi level in the conduction band as compared to PuO2 material. When we studied the states of both materials, an interesting feature is observed during the phase shift of spins that clear energy gap can be observed in the case of PuO2, while for the AmO2 a minor gap in energy has been found. More or less, all properties of both compounds are same, except for 5f states, which make AmO2 material more stable and radioactive as compared to PuO2 material. The crystal field splitting shows the energy gap for eg and t2g states. The value of crystal field splitting is 3.2 and 4.6 eV for AmO2 and PuO2 materials, respectively.