Keywords
|
| AES, cryptanalysis. |
INTRODUCTION
|
| In today’s scenario people share information to another people by use of network due to this more amount of information are so much private but some are less private due to this the attacker or the hackers are taking advantage and they are attempting to steal the information to overcome various used since 2001 since it provides high level of security and can be implementation easily. |
RELATED WORK
|
| The first open encryption algorithm, Data Encryption Standard (DES) was adopted by the National Institute of Standards and Technology(NIST) to protect the sensitive information as Federal Information Processing Standard 46 (FIPS PUB 46) in 1977 [1]. However, the shorter length of key, the complementary property and existence of weak and semi-weak keys reduce the security of DES. Differential cryptanalysis attack is capable of breaking DES in less than 255 complexities. The linear cryptanalysis method can find a DES key given 2 43 known plaintexts, as compared to 247 chosen plaintexts for differential cryptanalysis. So, it was more essential to find a stronger encryption algorithm to substitute the DES.In spite of the vulnerability of DES to a brute-force attack, there has been considerable interest in finding an alternative. One approach is to design a completely new algorithm and another alternative would be the one that preserves the existing one by using multiple encryption with DES and multiple keys. Three other algorithms were found to solve the problems of DES. They are Double DES, Triple DES with two keys and Triple DES with three keys. The principal drawback of Triple DES is that it has three times as many rounds as DES and hence it is much slower. Triple DES uses a 64 bit block size which is another drawback because for both efficiency and security, a larger block size is desirable. Because of these drawbacks, Triple DES is not favorable for long term use.TheRijndael algorithm was adopted as an encryption standard, the Advanced Encryption System (AES) by the NIST as FIPS PUB 197 (FIPS 197) on November 2001 [2]. The AES algorithm was believed to provide more security than the DES [3]. The AES algorithm was designed to have resistance against all known attacks, speed and code compactness on a wide range of platforms and design simplicity [7]. AES has three variable key lengths but block length is fixed to 128 bits [2]. The three key sizes of AES are 128, 192 and 256 bits. Their number of possible keys is 3.4 x 10 38, 6.2 x 1057 and 1.1 x 1077 respectively [2]. There are on the order of 10 21 times more AES 128-bit keys than DES 56-bit keys. AES with 128-bit keys has stronger resistance to an exhaustive key search than DES. |
Drawbacks of AES 256
|
| Rijndael has very strong resistance against the differential cryptanalysis and linear cryptanalysis attacks since it used Wide Trail Strategy in its design [8]. Although these linear attacks are invalid for the AES, they have been extended in several ways for recent years and new attacks have been published that are relative to them [4-6, 9-11]. The newest attack combined boomerang and the rectangle attack with related-key differentials was introduced by E. Biham, et al. in 2005 [9]. It uses the weaknesses of few nonlinear transformations in the key schedule algorithm of ciphers, and can break some reduced-round versions of AES. It can break 192-bit 9-round AES by using 256 different related keys. Rijndael inherits many properties from Square algorithm. So, the Square attack is also valid for Rijndael which can break round-reduced variants of Rijndael up to 6 or 7 rounds (i.e.AES-128 and AES-192) faster than an exhaustive key search [6]. N. Ferguson et al. proposed some optimizations that reduce the work factor of the attack [5]. So, this attack breaks a 256-bit 9-round AES with 277 plaintexts under 256 related keys, and 2224 encryptions. |
EXISTING WORK
|
| Previously many hardware implementation were proposed and was implemented they are 128,192,256 bit. There various implementation for AES support the fact that different application required different implementation for the same algorithm. Some application has strict area requirement and a compact AES implementation will be very useful to provide security as in the some embedded system cases. On the other side, some application highly needed the most level of security that can be obtained without carrying about the area /time limitation. |
PROPOSED WORK
|
| For more security required for certain system so as more chip area is needed, and this is due to complex algorithm flow or by increasing the algorithm parameters that include the site and plaintext size. |
| This paper shows another variation of AES algorithm called as 512 bit. The aim of this paper is to present the AES 512 bit can be used when higher level of security throughput are required without increasing overall design area as compared to the original 128 bit AES algorithm.in the new algorithm consist of the structure which is similar to original AES algorithm but having slight difference is that the plaintext size and key size using input of 512 bit instead of 128 bit has impact on the whole algorithm structure, as it will be discussed in detail later on the procedure to generate the new 512 bit key will be presented as well. The AES algorithm consist of four major operations are performed during each round: byte substitution, shifting rows, mixing columns and finally adding the round key. AES 128 bit key is considered secure compared to other existing symmetric cipher algorithm. It is widely used in many application were the security is very important the new AES algorithm provides even more security and double throughput. More security comes from using larger key size, and more throughput comes from using four times larger block size that the block size used in the original AES. The only disadvantage of AES 512 is the need for more design area. |
| The proposed AES 512 algorithm has four main different byte based transformation. The first transformation is the byte substitution which substitutes the value of 512 bit and this is achieved via using parallel s-boxes. The second transformation is shifting rows that shift the rows of the output from previous step by an offset equal to the row numbered. The third transformation is mixing column, where each column of the output from previous step is multiplied by different value. The final transformation in the round is adding round key to the result of this round. |
AES 512 ARCHITECTURE
|
| The top level architecture of the AES 512 bits the plaintext and key size are 512 bits each (organized in bytes). The AES 512 algorithm processes the data in 10 rounds the resulting cipher text is also 512 bits. |
| More detail about each of transformation used in the AES 512 are described in the coming sub section. Where the key expansion procedure is explained a later since each round need its own key generation according to this procedure. |
Bytes Substitution
|
| The 512 bits input plaintext are organized in array of 64 bytes and are substituted by values obtained from substitution boxes. This is done to achieve more security according to diffusion-confusion Shannon’s principles for cryptographic algorithm design. |
| To overcome the overhead of the huge data size used (512 bits), the substitution boxes are implemented as lookup tables and accessed in parallel as shown in figure 1. |
Shift Row
|
| After the original 512-bit data is substituted with values from the S-boxes, the rows of the resulting matrix are shifted in a process called Shift Row transformation. What happened in this part is that the bytes in each row in the input data matrix will be rotated left. The number of left rotations is not the same in each row, and it can be determined by the row number. For example, row number zero is not shifted, the first row is shifted by one byte, and so on. |
| Now, and after the rows of the input data are rotated left by different offsets, an operation must be applied to the columns of the data matrix. The Mix Column transformation multiplies the columns of the data matrix by a pre-defined matrix. The AES-512 and original AES process the data in bytes basis. Each byte is considered as polynomials over GF (28) with 8 terms. To explain how the Mix Column works, we have to explain the concept of polynomials over GF (2n) in general and for GF (28) as example when n=8. |
| A binary extension field element Y (x) is a polynomial of degree less than n and greater than -1, (i.e. Y (x) XOR 0), and has coefficients in GF(2). The polynomial basis is one representation for the elements of GF (2n). The addition in GF (2n) corresponds to a polynomial addition, which is done as a bitwise logic exclusive OR operation between the two bit vectors being added. An irreducible field polynomial p(x) of degree n is used to reduce intermediate results in GF (2n). In other words, the polynomials are reduced mod p(x) through long division operation to keep their degree less than n |
| The Mix Column operation (shown in Figure 3) multiplies the columns in the data matrix with a fixed polynomial of a(x), given by: |
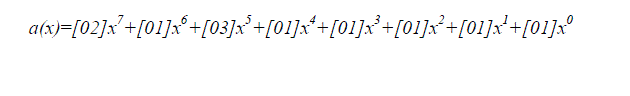 |
| The multiplication result is taken (modulo p(x) = x8 + 1) to keep the resulting polynomial with degree less than 8. |
| In the inverse of the Mix Column transformation, the input array is multiplied with the inverse of the polynomial a(x), denoted as a-1(x), which is given by: |
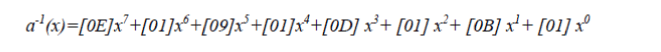 |
Add Round Key
|
| To make the relationship between the key and the cipher text more complicated and to satisfy the confusion principle, the Add Round Key operation is performed. |
| This addition step takes the resulting data matrix from the previous step and performs on it a bitwise XOR operation with the sub key of that specific round (addition operation in GF (2n)). We must mention that the round key is 512 bits that is arranged in a square matrix of eight columns where each column has 8 bytes. |
KEY EXPANSION AND ROUNDS
|
| The 512-bit input key of the new AES-512 algorithm is used to generate ten sub-keys for each of the ten AES rounds. The round ±keys expansion process involves arranging the original 512-bits input key into eight words of eight bytes each. After that, the round keys expansion is performed according to the following equations: |
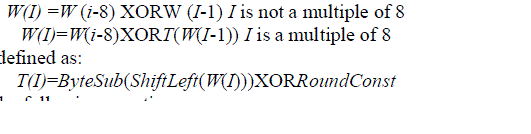 |
| The round constant is defined by the following equation: |
| RoundConst = 00000010(i-8)/8 |
| I is the round number |
| The round structure of the AES-512 algorithm (shown in Figure 4) uses the transformation defined in the previous section. First, byte substitution is performed on 512 bits data, followed by row rotation according to the row number, where 0-7 left rotations are performed in this step. Then, the columns are multiplied by the new defined matrix column by column in the Mix Column transformation (except in the 10th round). The last operation will be the bitwise XORing with the round key expanded using the key expansion process. The output at of the 10th round will be the 512-bit encrypted message. |
Analysis
|
 |
CONCLUSION
|
| Due to the increasing needs for secure communications, a more safe and secure cryptographic algorithms has to be proposed and implemented. The Advanced Encryption Standard (AES-128bit) is widely used nowadays in many applications. In this paper, we proposed a new variation of AES (AES-512) with 512-bit input block an 512-bit key size compared with 128-bit in the original AES-128 algorithm. A complete hardware implementation for the new AES-512 was also presented in this paper. After comparing the hardware implementation results, we found that our new design has about 230% throughput compared with the original AES-128 design. The larger key size make the algorithm more secure, and the larger input block increases the throughput. The extra increase in area can be tolerated and makes the proposed algorithm ideal applications in which high level of security and high throughput are required such as in multimedia communications. |
ACKNOWLEDGEMENTS
|
| We are profoundly grateful to Prof. Ghule S. J. for her expert guidance and continuous encouragement throughout to see that this project rights its target since its commencement to its completion. We are also grateful to Prof. Jadhav H. B. (Co-ordinator) for his support and guidance that have helped us to expand our horizons of thought and expression.We would like to express our deepest appreciation towards Dr. Nagrajan T. K., Principal, SCSCOE, Shrishivajinagar, Prof. Gade D. P., HOD Computer Engineering Department, whose invaluable guidance supported us in completion of the ofthis project. At last we must express our sincere heartfelt gratitude to all friends and staff members of Computer Engineering Department who helped us directly or indirectly during this course of work. |
Tables at a glance
|
 |
| Table 1 |
|
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
References
|
- S.Radhika, A.ChandraSekar ,“AES Algorithm Using 512 Bit Key Implemented For Secure Communication”, GJCST,Vol. 10 ,2010.
- Rohan Rayarikar, SanketUpadhyay, PriyankaPimpale, “SMS Encryption usingAES Algorithm on Android”, IJCA, Volume 50- No.19, 2012.
- Joan Daemen and Vincent Rijmen, “A Specification for Rijndael, the AES Algorithm”, Dr. Brian Gladman, v3.1, 2001.
- Ashwaq T. Hashim , “A Proposed 512 bits RC6 Encryption Algorithm”,IJCCCE,vol.10, no.1, 2010
- M.Anand Kumar and Dr.S .Karthikeyan ,“Investigating the Efficiency of Blow-fish and Rijndael (AES) Algorithms” ,I. J. Computer Network andInformation Security, 2012
- Nikolas Bardis, KonstantinosNtaikos, “Design of a Secure Chat Application basedOn AES Cryptographic Algorithm and Key Management”,2009.
- Hassan Mathkour, GhazyAssassa, A. Al-Muharib, A. Juma, “A Secured Cryp-tographic Messaging System”, International Conference onMachine Learning andComputing IPCSIT vol.3, 2011.
- Carlos Cid, Sean Murphy and Matthew Robshaw, “Computational and AlgebraicAspects of the Advanced Encryption Standard”, InformationSecurity Group, 2008.
- Zirra Peter Buba and Gregory MakshaWajiga, “Cryptographic Algorithms forSecure Data Communication”, International Journal ofComputer Science and Security (IJCSS), Volume (5),2011.
- Swati Paliwal, Ravindra Gupta, “A Review of Some Popular Encryption Techniques” ,IJARCSSE Volume 3,2013.
- AbidalrahamanMoh’d,Yaser Jaraweh,”AES-512: 512-Bit Advanced Encryption Standard Algorithm Design and Evaluation” InternationalConference on Information Assurance and Security (IAS) ,2011.
- J. Daemen and V. Rijmen, The Design of Rijndael: AES - The Advanced Encryption Standard",2009.
- H. Gilbert and M. Minier, A collision attack on seven rounds of Rijndael, Pro-ceding’s of the 3rd AES", pp.230-241, April 2000.
- S.Lucks, Attacking seven rounds of Rijndael under 192-bit and 256-bit keys",pp. 215-229, April 2000.
- G. Jakimoski and Y. Desmedt,\Related-Key Differential Cryptanalysis of 192-Bit Key AES Variants",vol. 3006, pp. 208-221, 2004.
- Willam Stallings, AtulKahate, Cryptography and Network Security" lectures and books, 2005.
|