An Efficient Transmission over Cooperative
Groups Using Hybrid Scheme

K.Banupriya

An Efficient Transmission over Cooperative Groups Using Hybrid Scheme

K.Banupriya
M.E CSE, M.A.R College of Engineering and Technology, Trichirapalli, Tamilnadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

The growth of group applications triggers the need for group-oriented security mechanisms over insecure network channels. The applications include IP telephony, collaborative work spaces, secure conferences, as well as dynamic coalitions common in law enforcement and disaster rescue scenarios. Standard security services required in such group settings, e.g., confidentiality of group-wide broadcasts can be very efficiently achieved if all group members share a group-wide secret key. The existing key management system used two approaches. One is Group key Agreement and another one is Key Distribution. Both approaches provided an unsecured data transmission and also very difficult to join a member in a remote system. It cannot deals with re-keying concept. In this paper, I proposed Hybrid of Group key agreement and public key broadcast encryption to Effective and Secure transmission of data to the remote cooperative groups. It provides fully secure data transmission and easy to join a new member in the existing system. In this approach, update the session key in a group easy.

Keywords

Group key agreement, key distribution, cooperative groups, session key, and broadcast.

INTRODUCTION

As a result of the increased popularity of group-oriented applications and protocols, group communication occurs in many different settings: from network layer multicast to application layer tele- and video-conferencing. Regardless of the underlying environment, security services are necessary to provide communication privacy and integrity. In many newly emerging networks, there is a need to broadcast to remote cooperative groups using encrypted transmission. Examples can be found in access control in remote group communication arising in wireless mesh networks (WMNs), mobile ad hoc networks (MANETs), vehicular ad hoc networks (VANETs), etc.

The common problem is to enable a sender to securely transmit messages to a remote cooperative group. A solution to this problem must meet several constraints. First, the sender is remote and can be dynamic. Second, the transmission may cross various networks including open insecure networks before reaching the intended recipients. Third, the communication from the group members to the sender may be limited. Also, the sender may wish to choose only a subset of the group as the intended recipients. Furthermore, it is hard to resort to a fully trusted third party to secure the communication. In contrast to the above constraints, mitigating features are that the group members are cooperative and the communication among them is local and efficient, and also reduces the computation overhead and the communication costs are independent of the group size. The paper is simple that contains the efficient member deletion/ addition and also contains the rekeying concept. This paper exploits these mitigating features to facilitate remote access control of group-oriented communications without relying on a fully trusted secret key generation center.

A. Related Work

The major security concern in group oriented communications with access control is key management. The existing key management systems used two approaches. One is Group key agreement (or group key exchange by some authors) which allows a group of users to negotiate a common secret key via open insecure networks. Then, any member can encrypt any confidential message with the shared secret key and only the group members can decrypt. And another one is key distribution systems (or the more powerful notion of broadcast encryption). In a key distribution system, a trusted and centralized key server presets and allocates the secret keys to potential users, such that only the privileged users can read the transmitted message. The early key distribution protocol [21] does not support member addition/deletion.

B. Contribution

Three aspects are important in our contribution. First, we formalize the problem of secure transmission to remote cooperative groups. We observe that the existing key management approaches do not provide effective solutions to this problem. On one hand, group key agreement provides an efficient solution to secure intragroup communication, but for a remote sender, it requires the sender to simultaneously stay online with the group members for multiple rounds of interactions to negotiate a common secret session key before transmitting any secret contents. On the other hand, broadcast encryption enables external senders to broadcast to noncooperative member s of a preset group without requiring the sender to interact with the receivers before transmitting secret contents, but it relies on a centralized key server to generate and distribute secret keys for each group member. This implies that: 1) before a confidential broadcast channel is established, numerous confidential unicast channels from the key server to each potential receiver have to be constructed; and 2) the key server holding the secret key of each receiver can read all the communications a n d has to be fully trusted by any potential sender and the group members

Second, we propose the new approach is a hybrid of group key agreement and public-key broadcast encryption. In our approach, each group member has a public/ secret key pair. By knowing the public keys of the members, a remote sender can securely broadcast a secret session key to any intended subgroup chosen in an ad hoc way and simultaneously, any message can be encrypted to the intended receivers with the session key. Only the selected group members can together decrypt the secret session key and hence the encrypted message. In this way, the dependence on a fully trusted key server is eliminated. Also, the dynamics of the sender and the group members are coped with because the communication between the sender and the receivers before the transmission of messages is avoided and the communication from the group members to the remote sender is minimized.

Third, The new key management paradigm and perform extensive experiments in the context of mobile ad hoc networks. In the proposed protocol, after extraction of the public group encryption key in the first run, the subsequent encryption by the sender and the decryption by each receiver are both of constant complexity, even in the case of member changes or system updates for rekeying. As to security, the proposal is shown secure against an attacker colluding with all the nonintended members. Even such an attacker cannot get any useful information about the messages transmitted by the remote sender. The proof is given under a variant of the standard Decision Diffie–Hellman (DDH) assumption.

II. PROBLEM STATEMENT AND SYSTEM MODEL

A. Problem Statement

A group composed of N users, indicated by {u1…uN}. A sender would like to transmit secret messages to a receiver subset S of the N users, where the size S of is n≤N. The problem is how to enable the sender to efficiently and securely finish the transmission with the following constraints.

1) It is hard to deploy a key generation authority fully trusted by all users and potential senders in open network settings.

2) The communication from the receivers to the sender is limited, e.g., in the battlefield communication setting.

3) N might be very large and up to millions, for instance, in vehicular ad hoc networks.

4) Both the sender and the receiver sets are dynamic due to ad hoc communication. According to the application scenarios, there are also some mitigating features that may be exploited for solving the problem.

1) n is usually a small or medium value, e.g., less than 256.

2) The receivers are cooperative and communicated via efficient local (broadcast) channels.

3) A partially trusted authority, e.g., a public key infrastructure, is available to authenticate the receivers (and the senders).

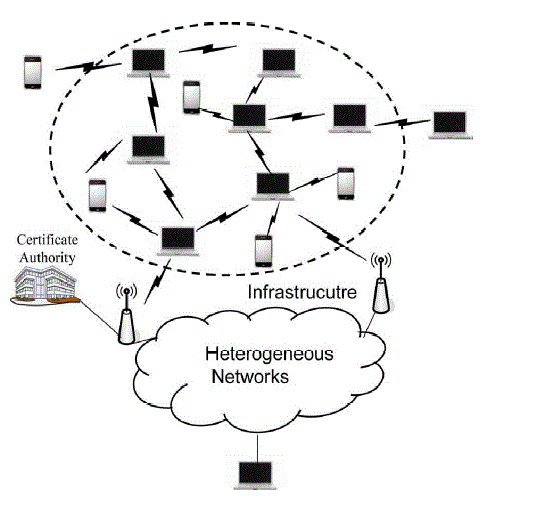
B. System Model

The potential receivers are linked together with efficient local connections. Using communication infrastructures, they can also join to heterogeneous networks. Each receiver has a public/secret key pair. The public key is certified by a certificate authority, but the secret key is kept only by the receiver. A remote sender can get back the receiver’s public key from the certificate authority and validate the authenticity of the public key by checking its certificate, which implies that no direct communication from the receivers to the sender is necessary. Then, the sender can send secret messages to any chosen subset of the receivers. We after that officially define the model of group key agreement based broadcast encryption. Since the heart of key management is to securely distribute a session key to the intended receivers, it is sufficient to define the system as a session key encapsulation mechanism. Then, the sender can at the same time encrypt any message under the session key, and only the intended receivers can decrypt.

III. KEY MANAGEMENT FOR TRANSMISSION TO REMOTE COOPERATIVE GROUPS

KeyGen: Each user i for i=1,..N randomly chooses

and computes

Encryption: Assume that a sender wishes to broadcast to users indexed by

The sender runs the following algorithm.

1) Randomly select

and compute

2) Extract the public group encryption key

3) Compute

4) Compute the secret session key

5) Broadcast the header

Decryption: The intended receivers run this algorithm as follows.

1) For j=1,…n, each receiver uij ∈s publishes

2) Each receiver indexed by ij can compute the secret decryption key

3) Using d , each receiver extracts the session key k from by computing k =e(d,c)

Hence,

This completes the correctness proof of the scheme.

IV. IMPLEMENTATION ISSUES

A. Member Organization

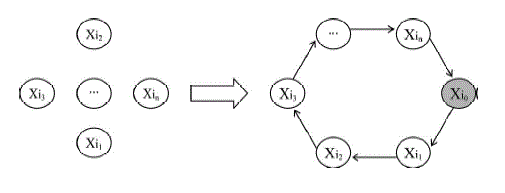
Several key management schemes arrange the users in a tree-based structure. However, for our proposal, it is preferable to organize them in a sequence and then use the sender to close the chain to form a logical ring. The chain can be formed by ordering the users lexicographically by the least important bits of their distinctive public keys.

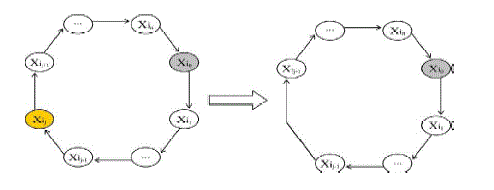
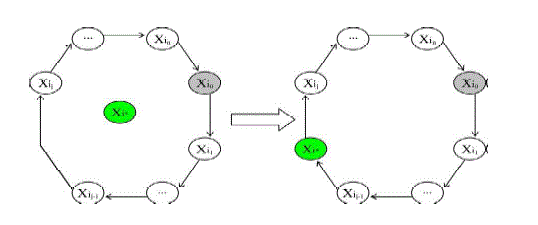
A. Member Deletion/Addition and Group Partition/Merging Member Deletion:

Encryption:

1) Randomly select

and

2) Compute the new public group encryption key

3) Compute

4) Compute the new secret session key

5) Broadcast to the receivers the new header

Decryption:

1) Only receivers

need to respond to the change in this step.

2) Compute the new group decryption key

3) Using d, each receiver extracts the new session

by computing k =e(d,c)

C. Re-keying

This approach can provide three levels of key update.

1. Session Key Update: This first level is to update the session key k. This key is used to encrypt digital contents to the receivers, and it expires after each session. To update the session key, the sender just needs to partially run Steps 1, 4, and 5 in the Encryption procedure. Receivers only need to execute Step 3 in the Decryption procedure. Note that Step 1 of is not necessary as the receivers have obtained d.

2. Group Decryption Key Update: The second level is to update the secret decryption key used by the receivers to compute the session key. To update the shared decryption key d, the sender only needs to run Steps 1 and 3–5 in the Encryption procedure.

Receivers only need to partially execute the three steps in the Decryption procedure.

3. Long-Term Secret Key Update: The third level is to update the secret key xi of user yi .

CONCLUSION

A new-fangled hybrid scheme is to allow send-and-leave broadcasts to remote cooperative groups without relying on a totally trusted third party. This scheme has been established secure in the normal replica. Methodical complexity psychoanalysis and extensive experiments show that this proposal is also efficient in terms of computation and communication.

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

References

L. Zhang, Q. Wu, A. Solanas, and J. Domingo-Ferrer, “A scalable robust authentication protocol for secure vehicular communications,” IEEETrans. Veh. Technol., vol. 59, no. 4, pp. 1606–1617, May 2010.

M. Burmester and Y. Desmedt, “A secure and efficient conference Key distribution system,”Adv. Cryptal.,vol.950, EUROCRYPT’94, LNCS, pp.275–286, 1995.

M. Steiner, G. Tsudik, and M. Waidner, “Key agreement in dynamic peer groups,” IEEE Trans. Parallel Distrib. Syst., vol. 11, no. 8, pp. 769–780,Aug. 2000.

M. Waldvogel, G. Caronni, D. Sun, N. Weiler, and B. Plattner, “The versa key framework: Versatile group key management,” IEEE J. Sel. AreasCommun., vol. 17, no. 9, p. 1614–1631, Sep. 1999.

Q.Wu, J. Domingo-Ferrer, and U. González-Nicolás, “Balanced trustworthiness, safety and privacy in vehicle-to-vehicle communications,” IEEETrans. Veh. Technol., vol. 59, no. 2, pp. 559–573, Feb. 2010.

Y. Amir, Y. Kim, C. Nita-Rotaru, J. L. Schultz, J. Stanton, and G. Tsudik, “Secure group communication using robust contributory key agreement,”IEEE Trans. Parallel Distrib. Syst., vol. 15, no. 5, pp. 468–480, May 2004.

Y.-M. Huang, C.-H. Yeh, T.-I.Wang and H.-C. Chao, “Constructing Secure group communication over wireless ad hoc networks based on avirtual subnet model,” IEEE wireless Commun., vol. 14, no. 5, pp. 71–75, Oct. 2007.

Y. Zhang and Y. Fang, “ARSA: An attack-resilient security architecture for multi-hop wireless mesh networks,” IEEE J. Sel. Areas Commun, vol.24, no. 10, pp. 1916–1928, Oct. 2006.