International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

An Efficient Uncertain Data Point Clustering Based On Probability–Maximization Algorithm

C.Deepika1, R.Rangaraj2
  1. Research Scholar, PG & Research, Department of Computer Science, Hindusthan College of Arts & Science, Coimbatore, India
  2. Associate Professor, PG & Research, Department of Computer Science, Hindusthan College of Arts & Science, Coimbatore, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Clustering on uncertain data, one of the essential tasks in mining uncertain data, posts significant challenges on both modelling similarity between uncertain objects and developing efficient computational methods. The existing methods extend traditional partitioning clustering methods like k-means and density-based clustering methods like DBSCAN and Kullback-Leibler to uncertain data, thus rely on numerical distances between objects. We study the Problem of clustering data objects whose locations are uncertain. A data object is represented by an uncertainty region over which a probability density function (pdf) is defined. The proposed method is based on the maximization of a generalized probability criterion, which can be interpreted as a degree of agreement between the numerical model and the uncertain clarification. We propose a variant of the PM algorithm that iteratively maximizes this measure. As an illustration, the method is applied to uncertain data clustering using finite mixture models, in the cases of categorical and continuous attributes. Our extensive experiment results verify the effectiveness, efficiency, and scalability of our approaches.

Keywords
Clustering, uncertain data, PM Algorithm, density estimation, Mixture Models.

INTRODUCTION
Recent years have seen a surge of interest in methods for managing and mining uncertain data [1], [2], [3]. As noted in [1], [4], [5], uncertain data arise in many applications due to limitations of the underlying equipment (e.g., unreliable sensors or sensor networks), use of imputation, interpolation or extrapolation techniques (to estimate, e.g., the position of moving objects), partial or uncertain responses in surveys, etc.
Clustering uncertain data has been well recognized as an important issue [6]. Generally, an uncertain data object can be represented by a probability distribution [7]. The problem of clustering uncertain objects according to their probability distributions happens in many scenarios.
For example, in marketing research, users are asked to evaluate digital cameras by scoring on various aspects, such as image quality, battery performance, shotting performance, and user friendliness. Each camera may be scored by many users. Thus, the user satisfaction to a camera can be modelled as an uncertain object on the user score space. There are often a good number of cameras under a user study. A frequent analysis task is to cluster the digital cameras under study according to user satisfaction data.
One challenge in this clustering task is that we need to consider the similarity between cameras not only in terms of their score values, but also their score distributions. One camera receiving high scores is different from one receiving low scores. At the same time, two cameras, though with the same mean score, are substantially different if their score variances are very different. As another example, a weather station monitors weather conditions including various measurements like temperature, precipitation amount, humidity, wind speed, and direction. The daily weather record
varies from day to day, which can be modelled as an uncertain object represented by a distribution over the space formed by several measurements. Can we group the weather conditions during the last month for stations in North America? Essentially, we need to cluster the uncertain objects according to their distributions.
In applications that require interaction with the physical world, such as location-based services [8] and sensor monitoring [9], data uncertainty is an inherent property due to measurement inaccuracy, sampling discrepancy, outdated data sources, or other errors. Although much research effort has been directed towards the management of uncertain data in databases, few researchers have addressed the issue of mining uncertain data. We note that with uncertainty, data values are no longer atomic. To apply traditional data mining techniques, uncertain data has to be summarized into atomic values. Unfortunately, discrepancy in the summarized recorded values and the actual values could seriously affect the quality of the mining results. Figure 1 illustrates this problem when a clustering algorithm is applied to moving objects with location uncertainty. If we solely rely on the recorded values, many objects could possibly be put into wrong clusters. Even worse, each member of a cluster would change the cluster centroids, thus resulting in more errors.
In recent work on uncertain data mining, probability theory has often been adopted as a formal framework for representing data uncertainty. Typically, an object is represented as a probability density function (pdf) over the attribute space, rather than as a single point as usually assumed when uncertainty is neglected. Mining techniques that have been proposed for such data include clustering algorithms [10], density estimation techniques [11], outlier detection [12], support vector classification [13], decision trees [5], etc.
Data is often associated with uncertainty because of measurement inaccuracy, sampling discrepancy, outdated data sources, or other errors. Data uncertainty can be categorized into two types, namely existential uncertainty and value uncertainty. In the first type it is uncertain whether the object or data tuple exists or not. For example, a tuple in a relational database could be associated with a probability value that indicates the confidence of its presence. In value uncertainty, a data item is modelled as a closed region which bounds its possible values, together with a probability density function of its value. This model can be used to quantify the imprecision of location and sensor data in a constantly-evolving environment.
This paper is organized as follows. In Section 2, provides Related work of the Density based clustering and Kmeans++ clustering. Section 3 presents the Collective Neighbor clustering algorithm. Section 4 illustrates the experiments and presents the results with some discussion. Finally, Conclusion our work in Section 5.

II. RELATED WORK
Clustering is a fundamental data mining task. Clustering certain data has been studied for years in data mining, machine learning, pattern recognition, bioinformatics, and some other fields [14], [15]. However, there is only preliminary research on clustering uncertain data.
A. Clustering Based on numerical Distances
Ngai et al. [16] proposed the UK-means method which extends the k-means method. The UK-means method measures the distance between an uncertain object and the cluster center (which is a certain point) by the expected distance. Recently, Lee et al. [17] showed that the UK-means method can be reduced to the k-means method on certain data points. UK-means basically follows the well-known K-means algorithm except that it uses expected distance when determining which cluster an object should be assigned to. The second algorithm uses the idea of min-max distance pruning in UK-means with the objective of reducing the number of expected distance calculations. UK-means starts by randomly selecting k points as cluster representatives. To calculate the integral, the distance of each sample to assigned cluster, and then approximate the integral by finding the sum of the distances, weighted by the corresponding probability density of the sample points. For accuracy, thousands of samples are needed. Expected distance calculation is thus a computationally expensive operation.
B. Clustering Based on sharing Similarity
The clustering distributions have appeared in the area of information retrieval when clustering documents [5]. The major difference of this work is that we do not assume any knowledge on the types of distributions of uncertain objects. When clustering documents, each document is modelled as a multinomial distribution in the language model. For example, Xu and Croft [18] discussed a k-means clustering method with KL divergence as the similarity measurement between multinomial distributions of documents. Assuming multinomial distributions, KL divergence can be computed using the number of occurrences of terms in documents. Dhillon et al. [19] used KL divergence to measure similarity between words to cluster words in documents in order to reduce the number of features in document classification. They developed a k-means like clustering algorithm and showed that the algorithm monotonically decreases the objective function as shown in [9], and minimizes the intra-cluster Jensen-Shannon divergence while maximizing intercluster Jensen-Shannon divergence. As their application is on text data, each word is a discrete random variable in the space of documents. Therefore, it is corresponding to the discrete case in our problem. The k-means like iterative relocation clustering algorithms based on Bregman divergences which is a general case of KL divergence. They summarized a generalized iterative relocation clustering framework for various similarity measures from the previous work from an information theoretical viewpoint. They showed that finding the optimal clustering is equivalent to minimizing the loss function in Bregman information corresponding to the selected Bregman divergence used as the underlying similarity measure. In terms of efficiency, their algorithms have linear complexity in each iteration with respect to the number of objects. However, they did not provide methods for efficiently evaluating Bregman divergence nor calculating the mean of a set of distributions in a cluster. For uncertain objects in our problem which can have arbitrary discrete or continuous distributions, it is essential to solve the two problems in order to scale on large data sets, as we can see in our experiments.

III. PROPOSED ALGORITHM
The proposed system is based on Maximum probability estimation from Uncertain Data clustering algorithm. We first describe an uncertain data model in which data uncertainty is represented by belief functions; this model encompasses probabilistic data, interval valued data and fuzzy data as special cases. The proposed system introduce an extension of the PM (Probability–maximization) algorithm, called the evidential PM (P2M) algorithm, allowing us to estimate parameters in parametric statistical models based on uncertain data. The proposed System shown in Fig. 1.
A. PM algorithm
The PM algorithm is a generally applicable mechanism for computing maximum probability estimates (MPEs) from incomplete data, in situations where maximum probability estimation would be straightforward. The complete EMAlgorithm Learning is listed in Algorithm 1.
The PM algorithm approaches the problem of maximizing the observed-data log likelihood log L(θ; A) by proceeding iteratively with the complete-data log probability log L(θ; x) = log px(x; θ). In each iteration of the algorithm involves two steps called the Probability step (P-step) and the maximization step (M-step).
The E-step requires the calculation of,
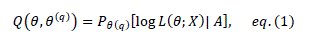image
Where θ(q) denotes the current fit of θ at iteration q and Pθ(q) [·|A] denotes probability with respect to the conditional distribution of X given A, using the parameter vector θ(q).
The M-step then consists in maximizing Q (θ; θ(q)) with respect to θ over the parameter space Ө, i.e., finding θ(q+1) such that Q(θ(q+1); θ(q)) ≥ Q(θ; θ(q)) for all θ Є Ө. The E- and M-steps are iterated until the difference L(θ(q+1); A)–L(θ(q); A) becomes smaller than some arbitrarily small amount.
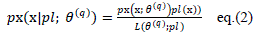image
where L(θ(q); pl) is discrete case, and (2) in the continuous case. At iteration q, the following function is thus computed: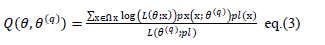image
in the discrete case, or 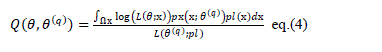image in the continuous case.
The M-step is unchanged and requires the maximization of Q(θ; θ(q)) with respect to θ. The E2M algorithm alternately repeats the E- and M-steps above until the increase of observed-data likelihood becomes smaller than some threshold.

IV. ALGORITHM 1: PSEUDO CODE
Input: Require: X, L, A, pl, θ and q
Output: The cluster output.
Require: A: Available cluster space, R: Resource (Data points), i (Iteration), S: Similarities.
Step 1: Initialize Q(θ), Q(X), px, Q(Ө), and Q(T) randomly
Step 2: repeat
Step 3: Update Q(X) is an arbitrary distribution on L.
Step 4: Update Q(θ) using eq.(1)
Step 5: Update px probability mass function using eq. (2)
Step 6: Calculate the value of log likelihood based on the probability densities using eq. (3)
Step 7: Create the clusters in discrete case by assigning each probability to a cluster such that the belonging probabilities are maximized using eq. (4)
Step 8: until convergence
Step 9: return Q(X) and px(x)
Step 10: End

V. SIMULATION RESULTS
The extensive experiments on both synthetic and real data sets to evaluate the effectiveness of PM algorithm as a similarity measure for clustering uncertain data and the efficiency of the techniques for evaluating PM divergences. The experiments were conducted on a computer with an Intel Core 2 Duo P8700 2.53 GHz CPU and 2 GB main memory running windows xp (sp2). All programs ran in-memory.
The data sets in both continuous and discrete domains. In the continuous case, an uncertain object is a sample drawn from a continuous distribution. In the discrete case, a data set is generated by converting a data set in the continuous case. We discretized the continuous domain by partitioning it into a grid. Every dimension is equally divided into two parts. So, a d-dimensional space is divided into 2d cells of equal size. We use the central points of cells as values in the discrete domain. The probability of an object in a cell is the sum of the probabilities of all its sample points in this cell.
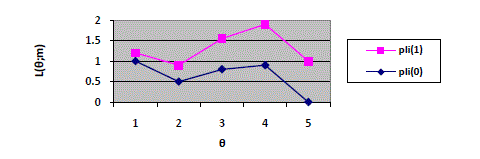
The above algorithm was applied to the data shown in Table 1. This dataset is composed of n = 6 observations, one of which (for i = 4) is uncertain and depends on a co-efficient. In that special case it is assumed that pl4(0) + pl4(1) = 1, i.e., the corresponding mass function mi is Bayesian.
The results are shown in Table 2 and 3. The algorithm was stopped when the relative increase of the likelihood between two iterations was less than 10-6. Starting from the initial value θ(0) = 0:3, this condition was met after 5 iterations. The final MLE is θ’ = 0:6. This is the value of θ that minimizes the conflict between the uncertain data given in Table 1.

VI. CONCLUSION
In this paper, the PM algorithm was motivated by our interest in uncertain data clustering of both discrete and continuous phase. We explore clustering uncertain data based on the similarity between their distributions. We advocate using the Probability–maximization algorithm as the probability similarity measurement, and systematically define the PM divergence between objects in both the continuous and discrete cases. We integrated PM divergence into the partitioning and density-based clustering methods to demonstrate the effectiveness of clustering using PM divergence.
Our proposed method then seeks the value of the unidentified parameter that maximizes a generalized probability criterion, which can be interpreted as an angle of agreement between the parametric model and the uncertain data. This is achieved using the evidential PM algorithm, which is a simple extension of the classical PM algorithm with proved convergence properties.

Tables at a glance
Table icon Table icon Table icon
Table 1 Table 2 Table 3
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
 

References