An Extremely Versatile Key Pre-Distribution Plan for Remote Sensor Systems

Abstract

A procedure that prevents attackers from fast in sequence from both sensor composed information and be submerged issued queries. SafeQ also allows a descend to sense compromised storage nodes when they behave badly. To protect privacy, SafeQ uses a novel technique to instruct both information and queries such that a storage node can correctly procedure prearranged queries over encoded data without expressive their values. To preserve integrity, We Use two schemes—one using Merkle hash trees and a different using a new data structure called neighborhood chains—to generate integrity verification information so that a sink can use this information to verify whether the outcome of a query contains exactly the data items that satisfy the query. To improve presentation, we use an optimization method using Bloom filters to decrease the communication cost between sensors and storage space nodes. Therefore, we propose an enhanced unital-based key pre-sharing scheme providing high network scalability and good key sharing probability about lower bounded by We conduct approximate analysis and simulations and balance our solution to those of existing methods for different criteria such as storage overhead, network scalability, network connectivity, common secure path length and network resiliency. Our results show that the proposed approach enhances the network scalability while providing high secure connectivity reporting and overall improved performance. Moreover, for an equal network size, our solution reduces significantly the storage overhead compared to those of existing solutions.

Keywords

Wireless sensor networks, security, key organization network scalability, secure connectivity coverage.

INTRODUCTION

The privacy- and integrity-preserving range query problem has been under investigated. The priorart solution to this problem was future by Sheng and Li in their recent seminal work. We call it the “S&L scheme.”

This scheme has two main find a drawbacks: 1) it allows attackers to logical estimation on both sensor collected data and sink issued queries; and 2) the power use and storage space for both sensors and storage nodes grow exponentially with the number of dimensions of collected data. In this paper, we use SafeQ, a novel privacy- and integrity-preserving range query protocol for two-tiered sensor networks. The ideas of SafeQ are fundamentally different from the S&L scheme. To preserve privacy, SafeQ uses a novel technique to encode both data and queries such that a storage space node can correctly process encoded queries over encoded data without knowing their actual values. To preserve integrity, we propose two schemes—one using Merkle hash trees and another using a new data structure called neighborhood chains—to generate integrity verification information such that a sink can use this information to verify whether the result of a query contains exactly the data items that satisfy the query. We also propose an optimization technique using Bloom filters to significantly Reduced the communication cost between sensors and storage nodes. also we propose a solution to adapt SafeQ for event-driven sensor networks, where a sensor submit data to its nearby storage node only when a positive event happens and the event may occur rarely Therefore, we propose an batter unitalbased key pre-distribution scheme that maintains a good key distribution probability while enhancing the network scalability. A introduction work and few discussions were presented in [13]. The contributions of our work are given next:

 We review the main state of the art of symmetric key management schemes for WSNs that we classify into two category: probabilistic schemes and deterministic ones. We further refine the classification into sub-categories with respect to the original concepts and technique used in key exchange and conformity

 We introduce, the use of unital design theory in key pre-distribution for WSNs. We show that the basic mapping from unitals to key pre-distribution gives birth to highly scalable scheme while only if low probability of sharing common keys.

 We propose an better unital-based key pre-distribution scheme in order to increase the network scalability while maintaining a good key distribution probability. We prove that adequate choice of our solution parameter should guarantee high key sharing probability about lower bounded by while ensuring a high network scalability.

 We analyze and compare our new approach against main existing schemes, with respect to different criteria: storage overhead, energy use network scalability, secure connectivity coverage, average secure path length and network resiliency.

II. UNITAL DESIGN FOR KEY PRE-DISTRIBUTION IN WSNS

WSNs are highly resource controlled. In particular, they suffer from reduced storage capacity. Therefore, it is essential to design stylish techniques to build blocks of keys that will be fixed on the nodes to secure the network links. Nonetheless, in most existing solutions, the design of key rings (blocks of keys) is powerfully related to the network size, these solutions either suffer from low scalability, or degrade other performance metrics including secure connectivity and storage overhead. This motivate the use of unital design theory that allows a smart construction of blocks with single features that allow to cope with the scalability and connectivity issues.In what follows, we start by providing the definition and the features of unital propose theory. We explain then the basic mapping from unital to key pre-distribution and assess its performance metrics. We propose finally an enhanced unital-based system which achieves a good trade-off between scalability and connectivity.

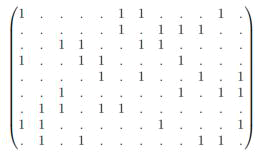Example of numbers matrix of a 2-(9,3,1) hermitian unital.

A.Background: Unital Design

In combinatorics, the design theory deals with the existence and structure of systems of finite sets whose intersections have specified numerical properties. Formally, A t-design (v,b,r,k, λ) s defined as follows : Given a finite set X of ν points (elements), we create a family of b subsets of X, called blocks, such that each block has a size k, each point is limited in r blocks and each t points are contained together in exactly λ blocks. For instance, the symmetric objective Incomplete Block Design (SBIBD) accessible above is a (v,b,r,k, λ) design, where

r=k=m+1 and λ=1

Without loss of generality, we center in this paper on Hermitian unitals which exist for all m a prime power. Other construction for m not necessarily a prime power exist in writing [19]. Some Hermitian unital construction approach were proposed in literature [20] [21].

A unital may be represent by its v*b incidence matrix that we call M. In this matrix rows represent the points pi and columns represent blocks Bj The matrix M is then defined as We give in Figure 2 an incidence matrix of a 2-(9,3,1) hermitian unital. It consists of 12 blocks of a set of 9 points. Each block contains 3 points and each point occurs in 4 blocks. Each pair of points is limited together in exactly one block.

B. A basic mapping from unitals to key pre-distribution for WSNs

this subsection, we start by developing a simple scalable key pre-distribution scheme based on unital design that we denote by NU-KP for the naive unital-based key pre-sharing scheme. We propose a basic mapping in which we link to each point of the unital a different key, to the international set of points the key pool and to each block a node key ring (see table III). We can then generate from a global key pool of keys, n key rings of size k = m+1 keys each one.

C.Theoretical analysis

Storage overhead: When using the proposed naive unital based story matching a unital of order m, each node is preloaded with one key ring matching to one block from the design, hence, each node is pre-full with (m +1) disjoint keys. The memory necessary to store keys is then l × (m+1) where l is the key size.

1. Network scalability: From construction, the total number of possible key rings when using the naive unital based scheme is

this is then the maximum integer of supported nodes.

2. Direct secure connectivity reporting: When using the basic unital mapping, we know that each key is used in exactly m2 key rings among the possible key rings.

III. A NEW SCALABLE UNITAL-BASED KEYPRE-DISTRIBUTION SCHEME FOR WSNS

In this section, we at hand a new unital-based key pre-distribution scheme for WSNs. In order to enhance the key sharing probability while maintain high network scalability, we propose to build the unital design blocks and pre-load each node with a number of blocks picked in a cautious way.

Key Pre-distribution:

Before the operation step, we generate blocks of m order unital design, where each block corresponds to a key set. We pre-load then each node with t totally disjoint blocks where t is a protocol parameter that we will discuss later in this section. In lemma 1, we demonstrate the condition of being of such t completely disjoint blocks among the unital blocks. In the basic draw near each node is pre-loaded with only one unital block and we proved that each two nodes divide at most one key. Contrary to this, pre-loading each two nodes with t displace unital blocks means that each two nodes share between zero and keys since each two unitals blocks share at most one constituent.After the consumption step, each two neighbors exchange the identifiers of their keys in order to determine the common keys. If two neighboring nodes share one or more keys, we suggest to compute the pairwise secret key as the hash of all their common keys concatenated to each other. The used hash function may be SHA-1 [22] for instance. This approach enhances the network resiliency since the attacker have to compromise more overlap keys to break a secure link. Otherwise, when neighbors do not share any key, they should find a secure path composed of consecutive secure links. The major advantage of this approach is the development of the key distribution probability. As we will prove in next subsection, this approach allows to achieve a high secure connectivity coverage since each node is pre-loaded with t disjoint blocks. Moreover, this approach gives good network resiliency through the composite pairwise secret keys which reinforces secure links. In addition, we show that our solution maintains a high network scalability compared to existing solutions although it remains lower than that of the naïve version.

IV. PERFORMANCE ANALYSIS

In this section, we compare the proposed unital-based schemes to existing schemes concerning different criteria.

A. Network scalability at equal key ring size

The scalability of the proposed unital based schemes against that of the SBIBD-KP and the Trade-KP ones. The network scalability of the t-UKP schemes is computed as the average value between the maximum and the least scalability. The network scalability of the SBIBD-KP system is computed as where m is the SBIBD design order and m +1is the key ring size. We compute the salability of the Trade-KP scheme as where q is the first prime power greater than the key ring size k, this value allows a achieve the best session key sharing probability using the Trade-KP scheme as we proved in [13]. The figure shows that at equal key ring size, the NU-KP scheme allows to enhance greatly the scalability compared to the other schemes; for instance the increase factor reaches 10000 compared to the SBIBD-KP scheme when the key ring size exceeds 100. Moreover, the figure shows that the t-UKP schemes achieve a high network scalability. We notice that the higher t is, the lower network scalability is. however, 2UKP and 3-UKP give enhanced results than those of the SBIBDKP and the Trade-KP solutions. Even we choose as we propose (UKP*), the network scalability is enhanced.

For instance, compared to SBIBD-KP scheme, the increase factor reaches five when the key ring size equal to 150. We plot in Figure 4 the same results discretely with linear scales which illustrate clearly the network scalability improvement when using our solutions.The authors of [3], assess the network scalability of random schemes including the RKP and the Q-composite ones regarding to the desired network connectivity and to the net- work capacity to maintain secure links while some nodes are compromised. They defined for that a threshold called the limited global payoff requirement. The later can be explained as the level of compromise past where the adversary gains an unacceptably information on the other pairwise secret keys. Depending on and they defined the maximum number supported network size. The authors of [3] present results for and show that the network scalability with a key ring size of 100 is about 300 for RKP scheme and between 600 and 700 when using Qcomposite schemes. The scalability of the same schemes with a key ring size of 400 is respectively of about 1200 and between 2700 and 2800. We can see clearly that our solutions allow to reach much better network scalability than the random schemes under the suggested parameters.

B. Key ring size at equal network size

In this subsection, we compare the required key ring size when using the unital-based, the SBIBD-KP and the TradeKP schemes at equal network size. We compute for each network size the design order allowing to achieve the desired scalability and we deduce then the key ring size, the obtained results are reported. The figure shows that at equal network size, the NU-KP scheme allows to reduce the key ring size and then the storage overhead. Indeed the improvement factor over the SBIBD-KP scheme reaches 20. When using the t-UKP schemes, the results show that the higher t is, the higher required key ring size is. However, this value remains significantly lower than the required key ring size of the SBIBD-KP and the Trade-KP schemes. Moreover, we can see clearly in the figure, that at equal network size, the scheme provides very good key ring size compared the SBIBD-KP and the Trade-KP schemes. For instance, the keyring size may be reduced over a factor greater than two when using the UKP* compared to the SBIBDKP scheme.

C.Energy consumption at equal network size

In this subsection, we evaluate the energy consumption induced by the direct secure link organization phase. Since each node broadcasts its list of key identifiers to its neighbors, the energy consumption can be computed as :

When is the average energy consumed by the transmission (resp. reception) of one bit, k is the key ring size, η is the average number of neighbors and represents the size of a key identifier in bits that we round up to the nearest byte size. We compare the energy consumption of our solutions against SBIBD-KP and Trade- KP. The results plotted show that at equal network size, the NU-KP scheme consumes very small amount of energy to exchange the low number of key identifiers. We also note that the higher t is, the higher the consumed energy is. This is due to the increased number of stored keys and thereby the enlarged number of exchanged identifiers. Finally, the figure shows clearly that UKP* scheme consumes less energy than the SBIBD-KP and the Trade-KP schemes. This matches our belief since the energy consumption is strongly correlated to the number of stored keys.

D. Network resiliency at equal key ring size

We compare in this section, the network resiliency of the unital-based schemes to those of the Trade-KP and the SBIBDKP ones. We observe that the proposed trade based construction given in [8] allows to have a unique pair-wise key per secure link, this key is computed as the hash of a unique pair of initial keys. However the overall network resiliency is not perfect because the compromise of some key rings may reveal other pairwise secret keys used to secure external links in which the compromised nodes are not involved. We proved that the resiliency of the Trade-KP scheme is given by: (see proof in appendix A)

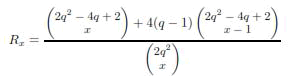where x is the number of comprised nodes and q is the Ruj et al. trade construction parameter. On the other hand, following the study presented in [10], the network resiliency of the SBIBD-KP scheme is given by:

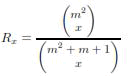Where m is the SBIBD design order. Finnaly, the network resiliency formula of unital based schemes was given in Proposition 3.We compare in Figure the network resiliency at equal number of compromised nodes for |KR| =68. The figure shows that the NU-KP scheme provides a good resiliency compared to other schemes. Using the t-UKP, the higher t is, the inferior network resiliency is at equal number of compromised nodes. This is due to the number of compromised unital blocks which is multiplied by t. On the other hand, the figure shows that the UKP* scheme improves the network resiliency over the SBIBD-KP scheme by 20%. It also gives a better network resiliency then the Trade-KP scheme when the number of compromised nodes exceeds 60.

E. Numerical results

We provide in table numerical results comparing network scalability, direct secure connectivity coverage, and average secure path length of the three schemes (SBIBD-KP, Trade-KP and UKP*) at equal key ring size. We notice that we provide the average network scalability (number of nodes) when using UKP* scheme. On the other hand, we compute the average secure path length based on simulations. We refer in these simulations to the consequences given in [23] in order to construct a grid deployment model which ensures the network physical connectivity and coverage. arithmetical results show that the unital-based key pre-allocation scheme UKP* increases the network scalability over the SBIBDKP and the Trade-KP scheme while maintaining high secure connectivity coverage. For instance, the network maximum size is increased by a factor of 3 and 4.8 when the key ring size is equal to 68 and 140 respectively compared to the SBIBD-KP scheme.

V. CONCLUSION

We make three key assistance. First, SafeQ, a novel and proficient protocol for handling rangequeries in two-tiered sensor networks in a privacy- and integrity-preserving fashion. SafeQ uses the techniques of prefix membership verification, Merkle hash trees, and neighborhood chaining. In terms of security, SafeQ significantly strengthens the security of two-tiered sensor networks. Second, an optimization technique using Bloom filters to significantly reduce the communication cost between sensors and storage nodes. Third, we propose a solution to adapt SafeQ for eventdriven sensor networks. We proposed, in this work, a scalable key organization scheme which ensures a good secure reporting of large scale WSN with a low key storage overhead and a good network resiliency. We make use of the unital design theory. We showed that a basic mapping from unitals to key pre-distribution allows to achieve high network scalability while giving a low direct secure connectivity coverage. We proposed then an efficient scalable unital-based key pre-distribution scheme providing high network scalability and good secure connectivity coverage. We discuss the solution parameter and we propose sufficient values giving a very good trade-off between network scalability and secure connectivity. We conducted analytical analysis and simulations to evaluate our new solution to existing ones, the results showed that our approach ensures a high secure exposure of large scale networks while provided that good overall performances.

Figures at a glance

Figure 1 Figure 2

References

1. Y. Zhou, Y. Fang, and Y. Zhang, “Securing wireless sensor networks: a survey,” IEEE Commun. Surv. Tuts., vol. 10, no. 1–4, pp. 6–28, 2008.
2. L. Eschenauer and V. D. Gligor, “A key-management scheme for distributed sensor networks,” in Proc. 2002 ACM CCS, pp. 41–47.
3. H. Chan, A. Perrig, and D. Song, “Random key predistribution schemes forsensornetworks,”inIEEE SP, pp. 197–213, 2003.
4. W. Du, J. Deng, Y. Han, S. Chen, and P. Varshney, “A key management scheme for wireless sensor networks using deployment knowledge,” in Proc. 2004 IEEE INFOCOM, pp. 586–597.
5. C. Castelluccia and A. Spognardi, “A robust key pre-distribution protocol for multi-phase wireless sensor networks,” in Proc. 2007 IEEE Securecom, pp. 351–360.
6. D. Liu and P. Ning, “Establishing pairwise keys in distributed sensor networks,” in Proc. 2003 ACM CCS, pp. 52–61.
7. Z. Yu and Y. Guan, “A robust group-based key management scheme for wireless sensor networks,” in Proc. 2005 IEEE WCNC, pp. 1915–1920.
8. S. Ruj, A. Nayak, and I. Stojmenovic, “Fully secure pairwise and triple key distribution in wireless sensor networks using combinatorial designs,” in Proc. 2011 IEEE INFOCOM, pp. 326–330.
9. S. Zhu, S. Setia, and S. Jajodia, “Leap: efficient security mechanisms for large-scale distributed sensor networks,” in Proc. 2003 ACM CCS, pp. 62–72.
10. S. A. C¸ amtepe and B. Yener, “Combinatorial design of key distribution mechanisms for wireless sensor networks,” IEEE/ACM Trans. Netw., vol. 15, pp. 346–358, 2007.
11. A. Perrig, R. Szewczyk, V. Wen, D. E. Culler, and J. D. Tygar, “Spins: security protocols for sensor netowrks,” in Proc. 2001 ACM MOBICOM, pp. 189–199.
12. B. Maala, Y. Challal, and A. Bouabdallah, “Hero: hierarchcal key management protocol for heterogeneous WSN,” in Proc. 2008 IFIP WSAN, pp. 125–136.
13. W. Bechkit, Y. Challal, and A. Bouabdallah, “A new scalable key predistribution scheme for WSN,” in Proc. 2012 IEEE ICCCN, pp. 1–7.
14. J. Zhang and V. Varadharajan, “Wireless sensor network key management survey and taxonomy,” J. Netw. Comput. Appl., vol. 33, no. 2, pp. 63–75, 2010.
15. S. A. C¸ amtepe and B. Yener, “Key distribution mechanisms for wireless sensor networks: a survey,” Technical Report TR-05-07, Mar. 2005.
16. R. Blom, “An optimal class of symmetric key generation systems,” in Proc. 1985 Eurocrypt Workshop Advances Cryptology: Theory Appl. Cryptographic Techniques, pp. 335–338.
17. T. Choi, H. B. Acharya, and M. G. Gouda, “The best keying protocol forsensornetworks,”inProc. 2011 IEEE WOWMOM, pp. 1–6.
18. S. Ruj and B. Roy, “Key predistribution using combinatorial designs for grid-group deployment scheme in wireless sensor networks,” ACM Trans. Sensor Netw., vol. 6, no. 4, pp. 1–4:28, Jan. 2010.
19. E. F. Assmus and J. D. Key, “Designs and their codes,” Cambridge Tracts in Mathematics. Cambridge University Press, 1992.
20. A. Betten, D. Betten, and V. D. Tonchev, “Unitals and codes,”” Discrete Mathematics, vol. 267, no. 1-3, pp. 23–33, 2003.
21. J. D. Key, “Some applications of magma in designs and codes: oval designs, hermitian unitals and generalized Reed-Muller codes,” J. Symbolic Computation, vol. 31, no. 1/2, pp. 37–53, 2001.
22. National Institute of Standards and Technology, Secure Hash Standard, Federal Information Processing Standards Publication, 1995.
23. S. Shakkottai, R. Srikant, and N. Shroff, “Unreliable sensor grids: coverage, connectivity and diameter,” in Proc. 2003 IEEE INFOCOM, pp. 1073–1083.
24. M. Doddavenkatappa, M. C. Chan, and A. L. Ananda, “A dualradio framework for MAC protocol implementation in wireless sensor networks,” in Proc. 2011 IEEE ICC, pp. 1–6.