An Optimization Model of Molecular Voronoi Cells in Computational Chemistry

Abstract

In computational chemistry or crystallography, we always meet the problem that requires distributing N particles in one square cell with the minimal neighbour distance. Sometimes this problem is with special or complex constraints. This short article will build a molecular optimization model for the problem, and then will show one example of the application of this model.

Keywords

Computational chemistry, crystal molecular structure, optimization model, optimized Voronoi cells distribution.

Introduction

We consider the problem that requires distributing N (≥ 1) particles in one three- dimensional (3D) 2a × 2b × 2c box/cell/unit with the minimal neighborhood distance. Let us define that dij is the directdistance variable between particle i (1 ≤ i ≤ N) and particle j (1 ≤ i ≤ N, j ≠ i).

Direct-distance means particles i and j have a direct interaction relationship, for example, in computational chemistry, VanderWaals (vdW) contact [1,2], (or) solvent accessible surface area (ASA) contact (en.wikipedia.org/wiki/Accessible surface area), etc to each other. Denote (x_i1, x_i2, x_i3) and (x_j1, x_j2, x_j3) the coordinates of particles i and j, respectively. Then, for the convenience of practical computations [3,4], we can build an optimization model for the above problem.

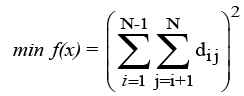(1)

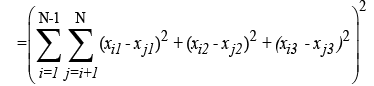(2)

Subject to −a ≤ x_i1, x_j1 ≤ a,−b ≤ x_i2, x_j2 ≤ b,−c ≤ x_i3, x_j3 ≤ c, i, j = 1, . . . ,N. (3)

This might be a problem of Voronoi diagram (en.wikipedia.org/wiki/Voronoi diagram) and the unit is called Voronoi cell. In computational chemistry, some crystals own special structures of the Voronoi cells; in such a case, we may add some additional constraints to Equation (3).

Clearly, the well-known Lennard-Jones Clusters problem [2] is one case of the above optimization problem Equations (1–3).

Example

We give a 2D Voronoi cells example Figure 1. We distribute 8 particles in one 2D square with the minimal neighborhood distance among them, with a constraint that each particle is only in one of the 8 Voronoi cells of the square. Figure 1(a) shows the initial solution that is given to the problem. Figure 1(b) and Figure 1(c) show the optimal (octagon) distribution of the 8 particles inner the square and onto the boundary of the square, respectively, after we solve the optimization problem Equations. (1-3) if in Equation. (3) “≤” is “≤” Figure 1(b) or “<” Figure 1(c).

Figure 1: The optimization model to distribute 8 particles into 8 Voronoi cells of a square unit: (a) initial distribution given, (b) optimal (octagon) distribution inner the square, and(c) Optimal (octagon) distribution onto the boundary of the square. The green dashed line denotes there is a direct relationship between the two particles they link (e.g. the two atoms have the vdW interactions).

Acknowlegements

This research was supported by a Victorian Life Sciences Computation Initiative (VLSCI) grant numbered VR0063 on its Peak Computing Facility at the University of Melbourne, an initiative of the Victorian Government (Australia).

References

1. Olechnovic K, et al. A fast and reliable tool for computing the vertices of the Voronoi diagram of atomic balls. J Comput Chem.2014;35:672-681.
2. Zhang JP. Thehybridideaofoptimizationmethodsappliedtotheenergy minimization of (prion) protein structures focusing on the ß2–a2 loop.Biochem Pharmacol(LosAngel) 2015
3. Zhang JP, etal. A novel canonicaldualcomputationalapproachforprion AGAAAAGA amyloidfibrilmolecularmodeling.JTheorBiol.2011;284:149–157.
4. Zhang JP. The LBFGS quasiNewtonian method for molecular modeling prion AGAAAAGA amyloid fib- rils. Nat Sci 4(12A) (Special Issue on Bioinformatics, Proteomics, Systems Biology and Their Impacts to Biomedicine). 2011;1:1097–1098.