Batch arrival Retrial G-queue and an
unreliable server with delayed repair

K. Kirupa; Dr. K. Udaya Ch; rika

Batch arrival Retrial G-queue and an unreliable server with delayed repair

K. Kirupa¹ and Dr. K. Udaya Chandrika²

Research Scholar, Department of Mathematics, Avinashilingam University, Coimbatore, Tamil Nadu, India
Professor, Department of Mathematics, Avinashilingam University, Coimbatore, Tamil Nadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Single server batch arrival retrial G-queue and an unreliable server with delayed repair are analyzed. Positive customers arrive in batches according to Poisson processes. If the server is idle, one of the positive customers in the batch enters for service while the rest join the orbit. Otherwise all the customers enter the orbit. Arrival of negative customer removes the positive customer being in service from the system and causes the server breakdown. The repair of the failed server starts after a random amount of time known as delay time. Expected system size, orbit size, availability and failure frequency of the server are derived. Stochastic decomposition law is verified. Numerical examples are presented to illustrate the influence of the parameters on several performance characteristics.

Keywords

Retrial queue, G-queue, server breakdown, delayed repair and stochastic decomposition.

INTRODUCTION

Queueing systems with repeated attempts are characterized by the fact that a customer finding all the servers busy upon arrival must leave the service area and repeat his request for service after some random time. Between trials, the blocked customers join a pool of unsatisfied customers called ‘orbit’. The retrial queueing system has been studied extensively due to its wide applicability in telephone switching system, telecommunication and computer networks. Recent works on retrial queue includes Aissani [1], Arivudainambi and Godhandaraman [2] and Artalejo and Li [3].

During the last decade, there has been an increasing interest in queueing system with negative customers. Queue with negative arrivals, called G-queue was first introduced by Gelenbe [5] with a view to modeling neural networks. Arrival of a negative customer induces positive customers to leave the system immediately. For a comprehensive analysis of queueing systems with negative arrivals, readers may refer to Gelenbe[6-8], Artalejo [4], Wu et.al [9] and Wu et.al [10]. In this paper, an unreliable batch arrival retrial G-queue with delayed repair is discussed.

MODEL DESCRIPTION

ANALYSIS OF THE STEADY STATE DISTRIBUTION

The system of equilibrium equations governing the model, using supplementary variable technique are given below:

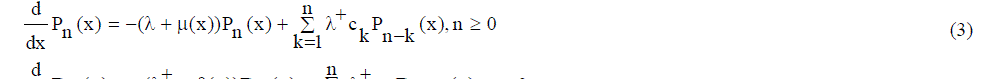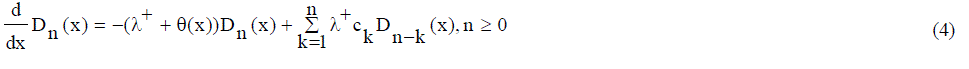The partial probability generating function of orbit size when the server is idle is given by

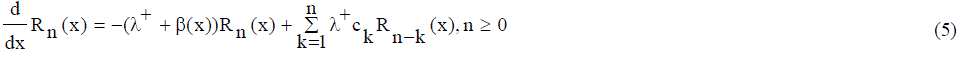Probability that the server is under repair is given by

STOCHASTIC DECOMPOSITION

NUMERICAL RESULTS

In this section, we give some numerical results to illustrate the effect of parameters on the performance characteristics. For numerical calculation, we assume that the distributions of service time, retrial time, delay time and repair time follow exponential with rate μ,η,θ and β.

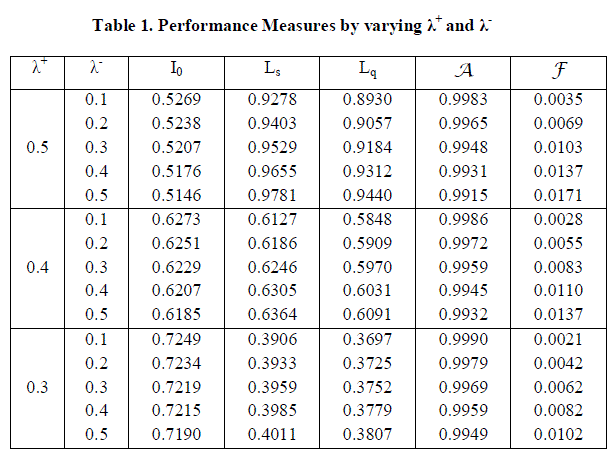
The effect of varying arrival rate λ+ and λ- with the fixed values (μ, η, θ, β) = (20, 0.5, 6, 3) on I0-probability that the server is idle in the empty system, Ls-Mean number of customers in the system, Lq -Mean number of customers in the orbit, A -Availability of the server and F - Failure frequency of the server is given in Table (1). From the table, it is clear that increase in λ+ and λ- , increases Ls ,Lq and decreases the other measures.

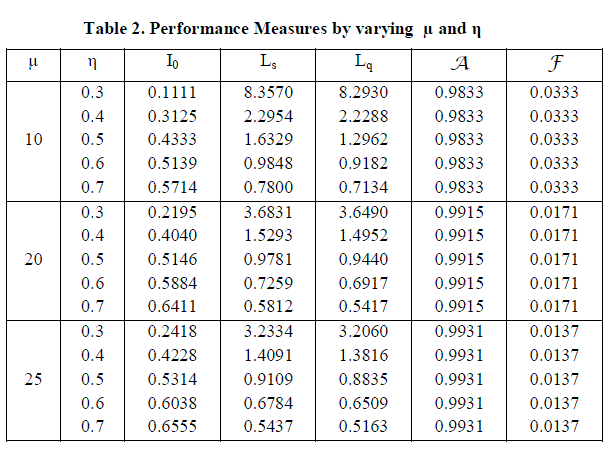
Table (2) provides I0,Ls,Lq, A and F by varying the values of μ and η for arbitrary values (λ+, λ-, θ, β)=(0.5, 0.5, 6, 3). Here, the table reveals that as μ and η increase, I0 increases, Ls and Lq decreases. As μ increase, A increases and F decreases.

Table (3) shows that the effect of varying θ and β with the fixed values (λ+, λ- , μ, η)=(0.5, 0.5, 20, 0.5) on the performance measures. From this table we observe that increase in β and θ, increases I0 and A, decreases Ls and Lq and has no effect on F.

References

Aissani, A., An MX/G/1 Energetic Retrial Queue with Vacations and Control, IMA Journal of Management Mathematics, 22, 13-32,2011.
Arivudainambi, D. and Godhandaraman, P., A Batch Arrival Retrial Queue with Two Phases of Service, Feedback and K Optional Vacations, Applied Mathematical Sciences, 6(22), 1071-1087, 2012.
Artalejo, J.R. and Li, Q., Performance Analysis of a Block Structured Discrete Time Retrial Queue with State Dependent Arrivals, Discrete Event Dynamic Systems, 20(3), 325-347, 2011.
Artalejo, J. R., G-networks: a versatile approach for work removal in queueing networks. European Journal of Operational Research ,126 , 233-249, 2000.
Gelenbe, E., Randomneural networks with negative and positive signals and product form solution. neural computation, 1, 502-510, 1989.
Gelenbe, E., Product-form queueing networks with negative and positive customers. Journal of applied probability,28 , 656-663, 1991.
Gelenbe, E., G-networks: a unifying model for neural and queueing networks. Annals of Operations Research, 48 , 433-461, 1994.
Gelenbe, E., The first decade of G-networks. European Journal of Operational Research, 126 , 231-232, 2000.
Wu, J., Liu, Z. and Peng, Y., Analysis of the finite source MAP/PH/N retrial G-queue operating in a random environment. Applied Mathematical Modelling 35 , 1184-1193, 2011.
Wu, J and Yin, X., An M/G/1 retrial G-queue with non-exhaustive random vacations and an unreliable server. Computers and Mathematics with Applications ,62 ,2314-2329, 2011.