Classical Viterbi algorithm (HOVA) and Soft Output Viterbi Algorithms (SOVA) are used for error correction in many applications. Among FEC schemes, convolutional encoding and Viterbi decoding are the most popular because of their powerful coding-gain performances. In this paper the performance analysis of Convolutional encoder and hard decision Viterbi algorithm and SOVA Bit Error Rate (BER) have been analyzed as well as compared considering different constraint lengths, generator polynomials. The rate considered is ½ rate for both the algorithms.
Keywords |
| FEC, Viterbi Decoder, SOVA, Generator polynomial, Trellis diagram |
I. INTRODUCTION |
| Encoding the information sequence prior to transmission implies adding extra redundancy to it, which is then used at
the receiver end to reconstruct the original sequence, effectively reducing the probability of errors induced by a noisy
channel. Different structures of codes have developed since, which are known as channel coding. Convolutional codes
[1] are a type of Error Correcting Codes (ECC) widely used in channel coding since the late 1960’s [2]. They are
preferred for their powerful correcting capability with high speed at low cost compared with their competing block
codes [3]. Other types include error detecting codes, which only detect errors and request for retransmission; however,
these types are more complex and expensive, as they require a two-way transmission system. |
| There have been a few convolutional decoding methods such as sequential and Viterbi decoding, of which the most
commonly employed technique is the Viterbi Algorithm (VA) [4, 5]. Viterbi decoding was developed by Andrew, J,
Viterbi, the founder of Qualcomm Corporation [6]. |
| Evaluation process of convolutional encoder and decoder (CODEC), for the various constraint lengths and for
different generator polynomials is discussed considering only few bytes of data [7]. The performance is analysed for
the burst errors and distributed errors. Impact of constrain length for the different input images for SOVA algorithm is
presented in [8]. A high performance generic soft input hard output Viterbi decoder is presented [9] and prototyped on
an FPGA board. The presented Viterbi decoder is intended to be used in a complete wireless LAN transceiver
prototype. |
| Viterbi decoding method uses the Maximum Likelihood Decoding (MLD) algorithm, this method find a most likely
pattern from the received data, and is known as the most optimum decoding method. In the proposed work the code rate
½ is used. The performance of Viterbi decoders are analysed for the different constraint lengths (CL) as well as for
different generator polynomials. |
II. RELATED WORK |
| Error recovery capability of convolutional CODEC is discussed in [10]. FPGA implementation of Viterbi decoder is
discussed in [11], paper concludes that the use of error-correcting codes have proven to be an effective way to
overcome data corruption in digital communication channels. Analysis of constrain length and generator polynomials
choice impact on the performance of convolutional CODEC in AWGN channel for image applications is presented in
[8]. The performance of Soft Output Viterbi decoding Algorithm (SOVA) has been discussed with the simulation
results in [13]. SOVA for the various constraint lengths and for different generator polynomials are simulated and
discussed. Performance of SOVA for burst and random errors are also tested in [13]. A high performance generic soft
input hard output Viterbi decoder is presented in [14] and prototyped on an FPGA board. In this paper the performance
comparison of SOVA and HOVA is done. |
III. PROPOSED ALGORITHM |
| The model considered for the simulation is shown in Fig.1. The channel considered is AWGN channel. At the
receiver side two types of Viterbi algorithm methods; hard decision decoder and SOVA are simulated. The different
generator polynomials, different constraint lengths are considered for convolutional coding and as well as for
decoding. |
| The performance measure parameter used is BER for different SNRs. Performance analysis is done in terms of BER
for different constraint lengths, generator polynomials and comparison is also shown. |
IV. SIMULATION MODEL |
| Convolutional codes are commonly specified by three parameters; (n, k, m). Where ‘n’ is the number of output bits,
‘k’ is the number of input bits considered at a time and ‘m’ is the number of memory registers. The quantity k/n called
the code rate is a measure of the efficiency of the code. Convolutional encoder consists of a shift register with ‘m’
memory registers, and ‘n’ modulo-2 adders interconnected. |
| A. Convolutional Encoder |
| Convolutional encoding is accomplished using a combination of simple shift register and modulo-2 adders. In
systematic style of encoding the input bits are included in the output stream along with the parity bits generated. Fig. 2
shows a ½ rate non-systematic convolutional encoder with constraint length 3. It makes use of two generator
polynomials (g1, g2) for calculating two output bits (P1k, P2k) for every input bit (Xk) considered. Inputs to the mod-2
adder (which generates P1k, P2k) are decided by g1 and g2 |
| B. Viterbi Decoder |
| Using the next-state table and output table a trellis for HOVA may be drawn as shown in Fig. 3. The Viterbi
decoder makes use of this trellis diagram to calculate most probable input sequence. The zero input is represented by
dotted line and one input is represented by the solid line in the Fig 3. There are two branches leaving and entering each state. Each branch is labelled with the corresponding outputs. In general case of (n, k, m) code and an information
sequence of length kL, there are 2k branches leaving and entering each state, and 2kL distinct paths through the trellis
corresponding to the 2kL code words. The decoder must produce the estimate of code word V
of the code word v based
on the received sequence r. A MLD for a discrete memory less channel (DMC) chooses V
as the code word v which
maximizes the log-likelihood function log P(r|v). Since for a DMC |
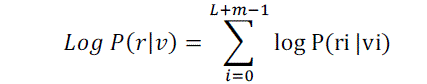 (1) (1) |
| Where P (ri|vi) is a channel transition probability. The log-likelihood function log P (r|v) is called the metric
associated with the path v, and is denoted M(r|v). The terms log P(ri|vi) in the sum (1) is called branch metrics and
denoted by M(ri|vi). The Viterbi decoder algorithm works as follows: |
| 1. Compute the partial metric for the single path entering each state in the Fig. 3 up to stage b. |
| 2. Compute the partial metric for all the paths entering a state by adding the branch metric entering that state to the
metric of the connecting survivors at the preceding time unit. For each state store the path with the largest metric
(the survivor), together with its metric, and eliminate all other paths. |
| 3. Repeat the step 2 for all L+m stages. Stop |
| There are 2k survivors from time unit m through time unit ‘L’, one for each of the 2k states. After time unit ‘L’ there
are fewer survivors, since there are fewer states while the encoder is returning to the all-zero state. Finally, at time unit
L+m, there is only one state, the all-zero state and hence only one survivor, and the algorithm terminates. After trellis
construction is performed for the complete block of encoded data, trace back is performed for determining the decoded
output sequence. The basic idea is to start from a specific state (pre-defined or having the smallest path metric) and trace
the path leading to this state backwards in time to reconstruct the encoder input is a trace back length. |
| In concatenated decoding systems (series or parallel) it is common for one decoder to pass the reliability (confidence)
information about its decoded outputs so called soft outputs to a second decoder. The SOVA is a variation of the Viterbi
algorithm. This algorithm has two modifications over the classical Viterbi algorithm. First, the path metrics used to select
the maximum likelihood path through the trellis are modified to take account of a-priori information. Second, the
algorithm is modified to provide a soft output for each decoded bit. |
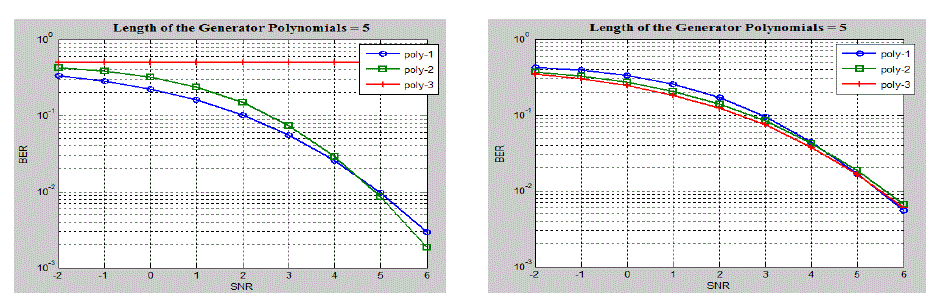
| Fig. 4a and Fig. 4b shows the BER performance of VD for the constraint length of five. Fig. 4a also shows the
performance for catastrophic polynomial. A decoder is said to exhibit catastrophic error-propagation when a finite
number of channel errors results in infinitely many decoding mistakes. Three different generator polynomials with the
constraint length of 5 are considered. The same set of inputs is considered for the three different polynomials
simulation. From these results it may be concluded that as the polynomial changes the BER performance also changes.
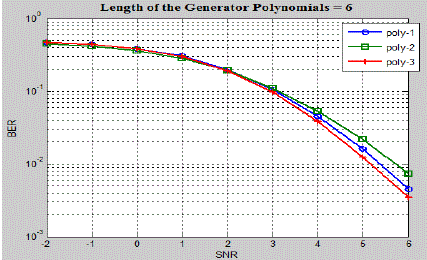
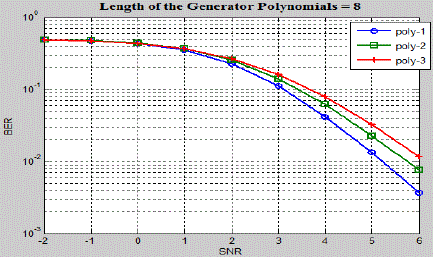
BER performance for the constraint length of six and eight are shown in Fig.5 and Fig.6 respectively. While choosing
the generator polynomial care should be taken to ensure that polynomial is not exhibiting catastrophic property. |
| From the simulation shown from Fig.4 to Fig.6 it may be concluded that the BER performance changes as the length of
generator polynomial changes it also changes from polynomial to polynomial. It is also observed that the decoding time
increases as the length of the generator polynomial increases. The simulations are also carried out for the SOVA for
different constraint lengths. |
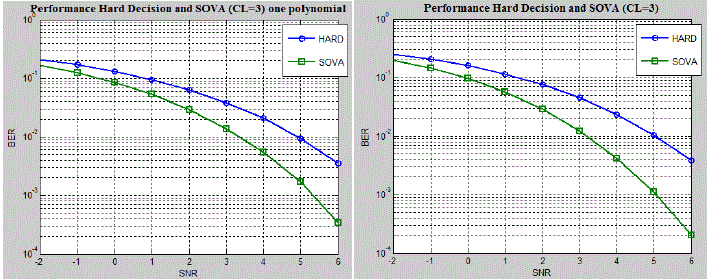
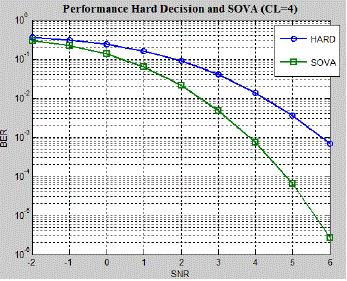
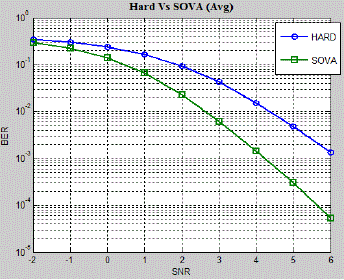
| Fig. 7a shows the BER performance of HOVA and SOVA for a same generator polynomial of constraint length of 3. In
the Fig.7b the average BER performance for three different generator polynomials for SOVA and HOVA are depicted.
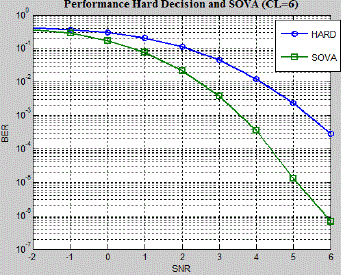
Fig.8 and Fig.9 shows the BER performance comparison between the two algorithms for the constraint length of 4 and
6 are shown. It may be observed that the SOVA BER performance is optimal compared to the HOVA in all the cases. |
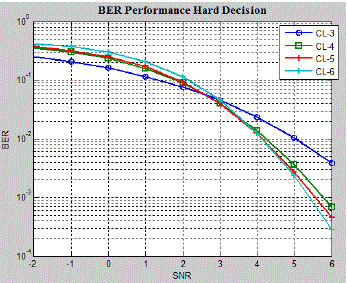
| The BER performance of HOVA for the different constraint lengths is plotted in the Fig. 10. For every constraint
length average BER performance of three different generator polynomials are considered. It may be observed that for
the low SNRs (Less than 2.7); lower constraint lengths are giving better results for higher SNR higher constraint
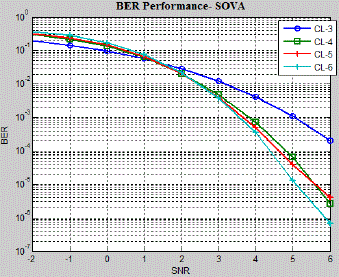
lengths are giving optimal performance. Similarly SOVA BER performances for different constraint lengths are plotted
in Fig.11. It may be observed that for the SNR more than one higher constraint length polynomials are giving optimal
results. Average BER shown in Fig.10 and Fig.11 are plotted in Fig.12. From the figure it may be concluded that BER
performance of SOVA is better compared to HOVA for any constraint lengths and for any generator polynomials. |
VI. CONCLUSION |
| In this paper, the effects of selection of constraint lengths, generator polynomials, on the performance of a HOVA
and SOVA have been investigated. By the simulation results it may be concluded that BER performances of Viterbi
decoders changes as the constraint length and generator polynomials changes. It is observed that the performance varies
with change in generator polynomial even for the same constrained lengths. So a good performing generator
polynomial for the given circumstances should be selected before proceeding. From the results it may be concluded that
the performance of SOVA is optimal compared to that of HOVA. |
Figures at a glance |
 |
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Figure 5 |
| |
 |
 |
 |
 |
 |
| Figure 6 |
Figure 7 |
Figure 8 |
Figure 9 |
Figure 10 |
| |
 |
 |
| Figure 11 |
Figure 12 |
|
| |
References |
- A. J. Viterbi, “Convolutional codes and their performance in communication systems”, IEEE Transaction Communication Technology, Vol.19,pp. 751-772, Oct. 1971.
- J. H. Yuen, “Modulation and Coding for Satellite and Space Communications”, IEEE Procedings, Vol. 78, No. 7, pp. 1250-1266, July 1990.
- B. Sklar, Digital Communications: “Fundamentals and Applications”, 2nd edition, Prentice-Hall, Upper Saddle River, N J, 2001.
- G. C. Clark Jr. and J. B. Cain, “Error-Correction Coding for Digital Communications”, Plenum Press, NY, 1981.
- A. J. Viterbi and J. K. Omura, “Principles of Digital Communications and Coding”, McGraw-Hill, NY, 1979.
- A. J. Viterbi, “Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm”, IEEE. Transaction ofInformation Theory, vol. IT-13, pp. 260-269, Apr. 1967.
- S.V.Viraktamath, Dr.G.V.Attimarad, V.P.Gejji, Ravi. H “Error Control Mechanism Using CODEC”, “International Conference onCommunication Software and Networks 2009” (ICCSN 2009), February 27 - 28, 2009. Macau, China. Page No 549; 978-0-7695-3522-7/09$25.00 © 2009 IEEE; DOI 10.1109/ICCSN.2009.142
- S.V.Viraktamath, Dr.G.V.Attimarad, “Impact of constraint length on performance of convolutional CODEC in AWGN channel for Imageapplications” has been published in “International Journal of Engineering Science and Technology (IJEST)”, Vol. 2(9), 2010, 4697-4701.ISSN: 0975-5462
- Abdulfattah Mohammad Obeid, Alberto Garc´ıa Ortiz, Ralf Ludewig and Manfred Glesner, “Prototyping of a High Performance GenericViterbi Decoder”, 13th IEEE International Workshop on Rapid System Prototyping (RSP’02).
- Hema .S, Suresh babu .V, Ramesh .P “FPGA Implementation of Viterbi Decoder” Proceedings of the 6th WSEAS Int. Conf. on Electronics,Hardware, Wireless and Optical Communications, Corfu Island, Greece, February 16-19, 2007 page no 162
- Jeich Mar. Senior Member, IEEE, Chi-Chenng KnL “Performance Improvement of a High Mobility Vehicular Communication Systemn Using Fuzy-Decision Viterbi Decoder” 2006 6th International Conference on ITS Telecommunications Proceedings page 1083
- S.V.Viraktamath, G.V.Attimarad, “Performance Analysis of SOVA for Random Bit stream”, 2010 IEEE International Conference onComputational Intelligence and Computing Research. 978-1-4244-5967-4/10/$26.00 ©2010 IEEE.
- Abdul Fattah Mohammad Obeid, Alberto Garc´ıa Ortiz, Ralf Ludewig and Manfred Glesner “Prototyping of a High Performance Generic Viterbi Decoder”, Proceedings of 13 th IEEE International Workshop on Rapid System Prototyping (RSP’02) 2002
|