1Sir Ratan Tata Trust Fellowship Institute of Economic Growth, Delhi University Enclave, New Delhi, India
2School of Management, The NorthCap University, Sector 23A, Gurgaon 122017, India
Received date: 15/04/2017; Accepted date: 29/04/2017; Published date: 30/04/2017
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
The Cauchy-Schwarz inequality is one of the most famous inequalities in mathematics. Over the period of time, it has been manifested in various forms and there are many different ways to prove this inequality. In this paper, we achieve one more proof to this inequality by making use of two basic statistical techniques, namely the coefficient of correlation and the coefficient of determination.
Cauchy-Schwarz inequality, another proof, Probability, Calculus
Over the years, the Cauchy-Schwarz inequality has made a prominent place in applied sciences. This inequality was first time jotted down in the form of finite sums by French mathematician Augustin-Louis Cauchy (1789-1857), in his work Cours d’analyse de l’École Royal Polytechnique, first published in 1821. Later on, in 1859, Cauchy’s former student from Russia, Viktor Yakovlevich Bunyakovsky (1804-1889), proved the inequality for infinite sums, and was written first time as integrals. The proof was published in the journal Mémoires de l’Académie Impériale des Sciences de St-Pétersbourg. Again, in 1888, Karl Hermann Amandus Schwarz (1843-1921), unaware of the work of Bunyakovsky, presented an independent proof of Cauchy’s inequality in integral form. Such an evolution of the inequality is the main reason behind its several names in literature, for example Cauchy- Schwarz, Schwarz, and Cauchy-Bunyakovsky-Schwarz inequality. The inequality, along with its extensions and generalizations, has been applied in diverse fields of mathematics and physics, such as partial differential equations, multivariable calculus, linear algebra, geometry, probability theory, operator theory and matrix analysis, uncertainty principles of Heisenberg and Schrӧdinger, etc [1-5]. This wide variety of applications of Cauchy-Schwarz inequality created its numerous manifestations and forms. The most prominent ones are:
The classical Cauchy-Schwartz Inequality states that if ai, bi (i=1, 2, 3,…..n) are real quantities i.e., ai, bi 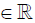 then,
then,
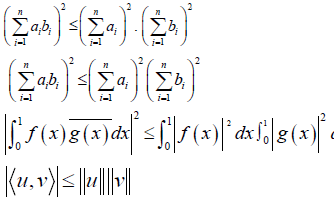
The various forms of Cauchy-Schwarz inequality has resulted in a number of proofs. In fact, there are many different ways to prove this inequality [6,7]. For instance, Wu and Wu [8] present twelve different proofs for the classical Cauchy-Schwarz inequality. In this paper, we make use of statistical techniques, namely the coefficient of correlation (r) and coefficient of determination (r2) to achieve this proof. To the best of our knowledge, such a kind of proof of this inequality has not been provided till now. Accordingly, it serves a good contribution to the existing literature.
Proof
Suppose X and Y are two random variables and, assuming their variances are positive, then the
correlation of (X, Y) is defined as
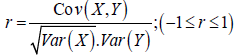
Squaring the coefficient of correlation gives coefficient of determination, which means
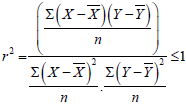
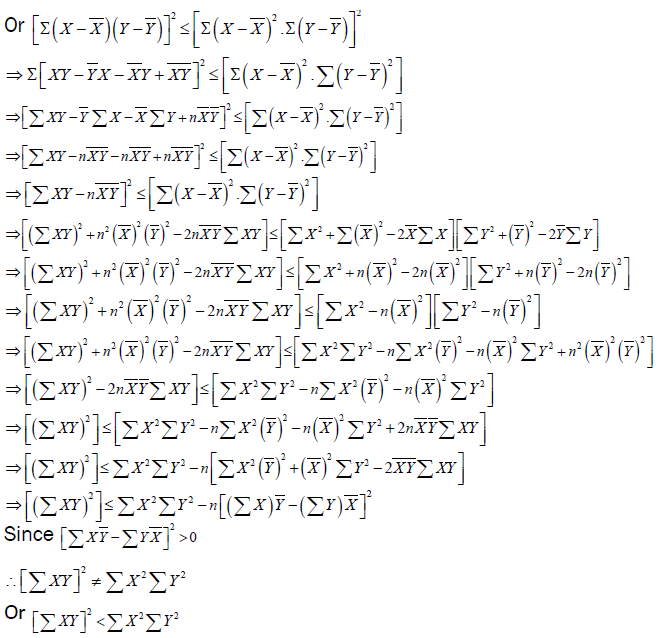
Hence proved.
The first author is mainly responsible for coming up with such an idea/proof. The second author executed the idea and put it in the present shape and form. The usual disclaimers apply.