Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Cluster Tree Based Hybrid Document Similarity Measure

M. Varshana Devi
PG Student, Department of CSE, V.S.B. Engineering College, Karur, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Cluster tree based hybrid similarity measure is established to measure the hybrid similarity. In cluster tree, the hybrid similarity measure can be calculated for the random data even it may not be the co-occurred and generate different views. Different views of tree can be combined and choose the one which is significant in cost. A method is proposed to combine the multiple views. Multiple views are represented by different distance measures into a single cluster. Comparing the cluster tree based hybrid similarity with the traditional statistical methods it gives the better feasibility for intelligent based search. It helps in improving the dimensionality reduction and semantic analysis.

Keywords
Dimensionality reduction, semantic analysis, cluster tree, hybrid similarity

INTRODUCTION
The evolution of human languages has been expedited by the use of the Internet. We see a growing demand for semantic representation that includes the term associations and spatial distributions. Another demand is to find lowdimensional semantic expressions of documents, while preserving the essential statistical relationships between terms and documents. Some usages of low-dimensional representation are extremely useful for facilitating the processing of large document corpora and the handling of various data mining tasks, such as classification, retrieval, plagiarism, etc. However, the main challenge for document analysis knows how to locate the low-dimensional space with the fusion of local information, which conveys term associations and spatial distributions, in a unified framework. Here, we introduce a new model for in-depth document analysis, named multidimensional latent semantic analysis (MDLSA). It starts by partitioning each document into paragraphs and establishing a term affinity matrix. Each component in the matrix reflects the statistics of term cooccurrence in a paragraph. It is worth noting that the document segmentation can be implemented in a finer manner, for example, partitioning into sentences. Thus, it allows us to perform an in-depth analysis in a more flexible way. We then conduct a 2-D principal component analysis (2DPCA) with respect to the term affinity matrix. This analysis relies on finding the leading eigenvectors of the sample covariance matrix to characterize a lower dimensional semantic space. According to our empirical study, we find that using only a 1-D projection to represent each document is sufficient to achieve marked results. Moreover, a hybrid document similarity measure is designed to further improve the performance of this framework. In comparison with the traditional “Bag of Words” (BoW) models such as the latent semantic indexing (LSI) and the principal component analysis (PCA), MDLSA aims to mine the in-depth document semantics, which enables us to not only capture the global semantics at the whole document level, but also to deliver the semantic information from local data-view regarding the term associations at the paragraph level. The problems in these methods are overcome by the cluster tree. The results corroborate that the proposed technique is accurate and computationally efficient for performing various document applications.

EXTRACTING GLOBAL FEATURES
In this section, we introduce the common procedures of document feature extraction, such as pre-processing, vocabulary construction, forming a weighted term vector, which is regarded as a global representation of a document, and dimensionality reduction.

Vocabulary Construction
First, we introduce the common document feature extraction procedures. The preprocessing works by first separating the main text contents from documents, for example, HTML formatted documents. We then extract words from all the documents in a dataset and apply stemming to each word. Stems are often used as basic features instead of original words. Thus, “program,” “programs,” and “programming” are all considered as the same word. We remove the stop words (a set of common words like “a,” “the,” “are,” etc.) and store the stemmed words together with the information of the tf, ft u(the frequency of the uth word in all documents), and the document frequency, fd u (the number of documents the u-th word appears). Forming a histogram vector for each document requires the construction of a word vocabulary each histogram vector can refer to. Based on the stored tf and document frequency, we use the wellknown tf-idf term-weighting measure to calculate the weight of each word
Wu=ftu ∙ idf
where idf denotes the inverse-document-frequency that is given by idf = log2 (n/fdu ), and n is the total number of documents in a dataset. It is noted that this term-weighting measure can be replaced by other feature selection criteria. The words are then sorted in descending order according to their weights. The first m words are selected to construct the vocabulary M. According to the empirical study using all the words in the dataset to construct the vocabulary is not necessarily expected to deliver the improvement of performance because some words may be noisy features for some topics. We have conducted detailed experiments to evaluate the performance in terms of different options of the vocabulary size, i.e., the value of m.

Dimensionality Reduction
A document set can be represented by X = [x1, x2, . . . , xn ] ∈ Rm×n , which is a rectangular matrix of terms and documents. The desire of latent semantic analysis is to produce a set Y , which is an accurate representation of X, but resides in a lower dimensional space. Y is of dimension d, with d << m, and it is produced by the form
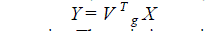image
where Vg is an m × d linear transformation matrix. Thus, it is straightforward to replace each document xi by its projection yi = VT g xi such that we can make between or within comparisons facile in the lower dimensional latent semantic space. There are a number of ways to accomplish this projection. The transformation matrix Vg can be obtained by traditional techniques such as the PCA, the LSI, or other dimensionality reduction approaches. In this study, we use the classical PCA to determine the matrix Vg. The PCA is a well-known technique in the category of dimensionality reduction. In the PCA, the determination of Vg is given by maximizing the variance of the projected vectors, which is in the format of
max - 22.
It has been shown that the matrix Vg is the set of eigenvectors of the sample covariance matrix associated with the d largest eigenvalues. Keep this in mind, as we will use this set of global representations {y1, y2, . . . , yn} to formulate a hybrid similarity of two documents.

WORD AFFINITY GRAPH
This section introduces a scheme to produce an in-depth document representation. First, we segment each document into paragraphs. Second, we build a word affinity graph, which describes the local information of each document.

Document Segmentation
As we mentioned before, the major drawback of the traditional modelling methods such as the PCA and the LSI is that they lack the description of term associations and spatial distribution information over the reduced space. In this study, we propose a new document representation that contains this description. First, each document is segmented into paragraphs. Since we only considered the HTML documents in this paper, a Java platform was developed to implement the segmentation. For the HTML format document, we can use the HTML tags to identify paragraphs easily. Before document segmentation, we first filter out the formatted text that appears within the HTML tags. The text is not accounted for in word counts or document features. The overall document partitioning process can be summarized as follows 1) Partition a document into blocks using the HTML tags: “<p>,” “<br\>,” “<li>,” “</td>,” etc. 2) Merge the subsequent blocks to form a new paragraph until the total number of words of the merged blocks exceeds a paragraph threshold (set at 50). 3) The new block is merged with the previous paragraph if the total number of words in a paragraph exceeds the minimum threshold (set at 30). For the HTML documents, it is noted that there is no rule for minimum/maximum number of words for paragraphs. Setting a threshold for word counts, however, still enables us to control the number of paragraphs flexibly in each document and remove the blocks, which contain only a few words (e.g., titles), by being attached to the real paragraph blocks. It is worth pointing out that we are able to further partition each paragraph into sentences by marking periods (the tag “/.”) to form a finer structure such that more semantics can be included.

Word Affinity Graph
Building a word affinity graph for each document is to represent the frequency of term cooccurrence in a paragraph. Consider a graph denoted by a matrix Gi ∈ Rm×m, in which each element gi,u,v (u, v = 1, 2, . . . , m) is defined by
gi,u,v=
where ||∙||2 is the Frobenius norm, Fu,v is the frequency of the cooccurrence in a paragraph associated with the terms u and v in the ith document, DFu,v is the document frequency that the terms u and v co appear in a document, and notations of ftu and fu.d cooccurrence in paragraphs, i.e., let gi,u,v = 0 (for u _= v), the affinity graph Gi becomes a diagonal matrix with the elements corresponding to the global feature vector xi shown in (2) (the NORM weighting). By definition, the graph Gi is a symmetric matrix. This graph contains the local semantic information of a document in a way that we can design an efficient semantic representation including term interconnections and distributions in a unified framework.

MULTIDIMENSIONAL LATENT SEMANTIC ANALYSIS
This section presents a new model, MDLSA, which considers word affinity graphs and maps them onto a lowdimensional latent semantic space. First, we introduce the objective of the MDLSA model. Second, we learn a semantic subspace by using the 2DPCA algorithm. Third, we further process and select the semantic projections. We summarize the MDLSA algorithm in the end.

Semantic Projection
Despite the capability of delivering more semantics, a word affinity graph is usually of large size and sparseness. It is computationally demanding if we simply rely on these graphs to make between or within comparisons. Besides, assembling the similarity between two matrices is another demanding issue. On the other hand, without further processing, these graph representations contain a large quantity of noises, which spread out the original term distributional space. As a result, these noises cause degradation of performance. Therefore, it is important to design an efficient dimensionality reduction technique, which is able to compress the graph in a principled manner and form an accurate representation in a lower dimensional space. The proposed MDLSA model is just this. Given a word affinity graph G of size m × m , the goal of MDLSA is to produce a projection ˜ Z of size d × d (d << m) resided in a lower dimensional semantic space. We then use a matrix Z of size d × k (k ≤ d), which is constructed by a smaller number of columns of ˜ Z. In linear algebra, the projection ˜Z can be obtained by
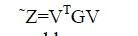image
where V is an m × d linear transformation matrix. The problem comes to finding an optimal transformation V for this dimensionality reduction.

Learning a Semantic Subspace
To acquire the optimal transformation matrix V , we use the 2DPCA method, which has been successfully implemented in a face recognition system. For completeness, the process of calculating the matrix V is summarized here, and the details can be found in the article reported by Yang et al. [25]. Let {G1,G2, . . . , Gn } be a set of training documents. By representing the word affinity graph Gi associated with the ith document, the graph covariance (or scatter) matrix C can be written by
C= (Gi-ˉG)
where ˉG denotes the average graph of all the training samples. Similar to PCA, 2DPCA introduces this total scatter of the projected samples to measure the discriminatory power of a transformation matrix V . In fact, the total scatter of the samples in a training set can be characterized by maximizing the criterion.
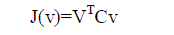image
where v is a unitary column vector, which is called the optimal mapping axis by maximizing the above quantity. In general, it is not sufficient to have only one optimal mapping axis. It is required to find a set of mapping axis, v1, v2, . . . , vd , subject to the orthogonal constraints and maximizing the criterion J(V ) by the form
{ v1, v2, . . . , vd}= arg max J(v) Subject to vjTvl =0(j≠l,j,l=1,2,...,d).
According to linear algebra, the optimal mapping axes, v1, v2, . . . , vd , are the orthogonal eigenvectors of C associated with the first largest d eigenvalues. If we denote these mapping axes by V = [v1, v2, . . . , vd , ] the projection ˜ Z of a word affinity graph G will be acquired easily by the product of the resulting matrices Here, note that we take advantage of the symmetry of the affinity graph G.

Selection of the Semantic Projections
Actually, we can use another matrix Z of size d × k (k ≤ d), which is a sub matrix of ˜ Z, to represent the original graph G for optimal approximate fit by discovering lower dimensional space. In practice, only using the first column of ˜ Z is sufficient to achieve remarkable results. Thus, the matrix Z is of size d × k (here, k = 1) and turns out to be a column vector like yi produced by the traditional PCA corresponding to the global feature xi . We also conducted an empirical study on the selections of value of k. To avoid confusion, in the following context, let zi be the first column of ˜ Zi , which denotes the projection matrix of the ith affinity graph Gi . Alternatively, the local information from the ith training document can be represented by the column vector zi . This is a very promising property of MDLSA by delivering three important advantages. First, in comparison with 2DPCA it does not need an assembled metric to conduct direct matrix comparison such that MDLSA is easier to make between comparisons. Second, much less time is required to compare two documents because MDLSA does not need the many-to-many matching compared with the MLM method. Third, MDLSA contains local semantic information of documents compared with the PCA and the LSI.

HYBRID DOCUMENT SIMILARITY
Many document applications rely on the calculation of similarity between two documents. In order to further improve the performance of our framework, we develop a hybrid similarity measure to synthesize the information from a global data-view and local data-view. In this study, we have extracted two sets of features from each document: a feature vector xi containing global information (i.e., tf) and an affinity graph Gi delivering local information (i.e., term associations). We then use dimensionality reduction techniques to map these features onto the latent semantic space, which is of lower dimension. Intuitively, combining these two information sources may bring performance gain. Therefore, we design a hybrid similarity associated with both the global and local information. Given two documents p and q, let yp be the latent representation of document p associated with the global feature xp , and zp the latent representation of document p produced from the local source Gp . Likewise, let yq be the latent representation of document q associated with the global feature xq , and zq the latent representation of document q produced from the local source Gq . We work by a combined similarity measure in the form, which involves the cosine distance criterion
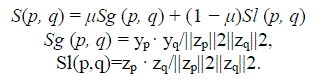image
where Sg (p, q) represents the global similarity, Sl (p, q) denotes the local similarity, and μ(0 ≤ μ ≤ 1) is a weight parameter used to balance the importance of the global and local similarity. Thus, the system provides users flexibility to select the value of μ to balance this hybrid measure according to their expectations. In this study, we also include the effect study of the parameter μ in experiments. Note that the local similarity S1(p, q) is associated with the features produced by only the MDLSA method, while the global similarity Sg (p, q) relies on the features obtained by the PCA.

CLUSTER TREE
When combining multiple views, we want to preserve cluster structures that are strongly suggested by the individual views. The idea is that if there was a strong separation between the data points in one of views, that separation should not be lost while combining the information from other views. In this it is proposed that building a hierarchical tree in a top-down fashion that uses the best view available at each split point in the tree.

CONCLUSION
The main focus on two common incapability of traditional statistics based semantic similarity measures for social tagging systems, e.g., unable to evaluate similarities among tags not co-occurred and unable to reflect the structural influence of the network of tag co-occurrence. Firstly, we propose a cluster tree based measure to evaluate the semantic similarity among random pair of tags. Secondly, we combine the cluster tree based measure and the statistics based measures into a hybrid one which can better reflect the structural influence of the network of tag co-occurrence.
 

References