ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Nishant Dhiman1, Abhishek Tyagi2 M.Tech, Department of Computer Engineering, Lovely Professional University ,Jalandhar,Punjab,India1 Assitant Professor, Department of Computer Engineering, Lovely Professional University, Jalandhar,Punjab India2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
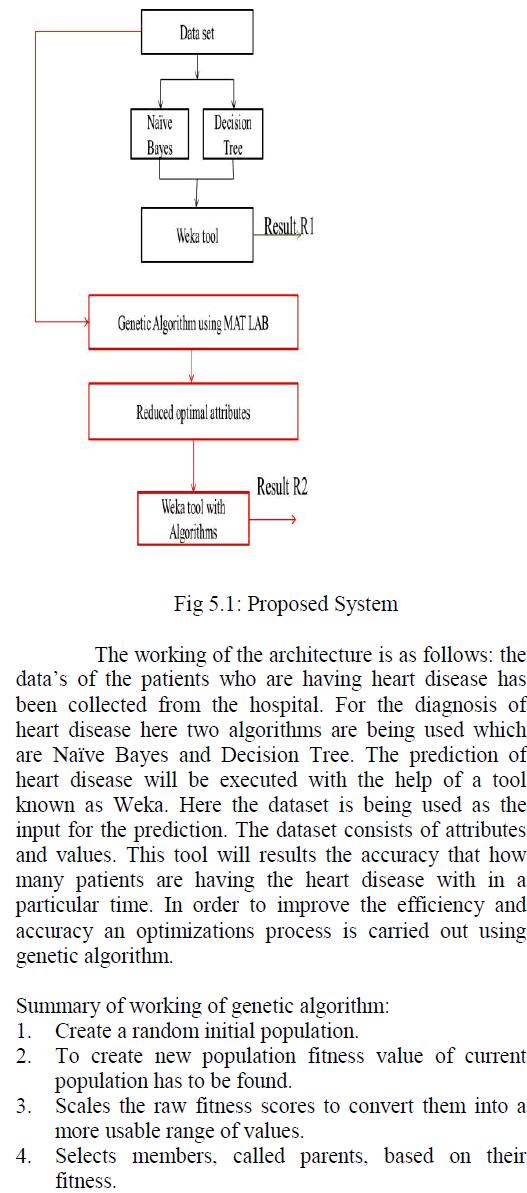
Data mining is the useful tool to discovering the knowledge from large database. For this we require proper classification methods & algorithms. In this paper, we are talking about the soil erection problem which can be removed with the help of proper clustering. C MEAN algorithm is one of the best techniques we have ever seen in data mining over a cluster but the problem with C MEAN is that, it lacks when you either use a very big data set or a small dataset. Hence in our research work, we will be implementing the ID3 ALGORITHM and will the check the accuracy terms with the C MEAN algorithm. Now our problem is to create a new group to check out whether the implemented algorithms can make any change in the accuracy if we increase the privacy level or not. The result of research tells us about the soil belongs to a fertilizing group.
Keywords |
| Data mining, classification algorithms, soil erection |
INTRODUCTION |
| Data mining is the extraction of hidden predictive information from large databases. It is a powerful new technology with great potential to help companies focus on the most important information in their data warehouses. Data mining tools predict future trends and behaviours, allowing businesses to make proactive, knowledge driven decisions. Three of the major data Mining techniques are regression, classification and clustering. .But in this we are using classification and clustering. The classification of the data is only possible if you have modified and identified the clusters. In the presented research work, our aim is to find out the maximum number of clusters in a specified region by applying the area searching algorithms. Classification is always based on two things, the area which you choose for the classification that is the cluster region and the kind of dataset which you are going to apply on the selected region. To increase the accuracy of the searching technique, any one would need to focus on two things whether the data set has been clusterized in proper manner or not, if the clusters are defined, whether they fit into the appropriate classified area or not. Clustering is the task of assigning a set of objects into groups (called clusters) so that the objects in the same cluster are more similar (in some sense or another) to each other than to those in other clusters. Clustering is a main task of explorative data mining, and a common technique for statistical data analysis used in many fields, including machine learning. pattern recognition, image analysis, information retrieval and bioinformatics [1]. |
II. CLASSIFICATION ALGORITHMS |
| In this paper for classification we are using the two algorithms. |
| A. K mean Algorithm |
| In data mining, k-means clustering is a method of cluster analysis which aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean. This result into a partitioning of the data space into Verona cells .K-means (Macqueen, 1967) is one of the simplest unsupervised learning algorithms that solve the well known clustering problem. The procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters) fixed a priori [6]. The main idea is to define k centroids, one for each cluster. These centroids should be placed in a cunning way because of different location causes different result. So, the better choice is to place them as much as possible far away from each other. The next step is to take each point belonging to a given data set and associate it to the nearest centroid. When no point is pending, the first step is completed and an early group age is done. At this point we need to recalculate k new centroids as bar centres of the clusters resulting from the previous step. After we have these k new centroids, a new binding has to be done between the same data set points and the nearest new centroid. A loop has been generated [5]. As a result of this loop we may notice that the k centroids change their location step by step until no more changes are done. In other words centroids do not move any more. The algorithm is composed of the following steps: |
| 1. Place K points into the space represented by the objects that are being clustered. These points represent initial group centroids. |
| 2. Assign each object to the group that has the closest centroid. |
| 3. When all objects have been assigned, recalculate the positions of the K centroids. |
| 4. Repeat Steps 2 and 3 until the centroids no longer move. This produces a separation of the objects into groups from which the metric to be minimized can be calculated. The problem is computationally difficult (NPhard), however there are efficient heuristic algorithms that are commonly employed that converge fast to a local optimum. These are usually similar to the expectation maximization algorithm for mixtures of Gaussian distributions via an iterative refinement approach employed by both algorithms [2]. |
| B. ID3 Algorithm |
| The ID3 algorithm is used to build a decision tree, given a set of non-categorical attributes C1, C2, .., Cn, the |
| categorical attribute C, and a training set T of records. |
| Function ID3 |
| (R: a set of non-categorical attributes, |
| C: the categorical attribute, |
| S: a training set) |
| Returns a decision tree; begin |
| If S is empty, return a single node with value Failure; |
| If S consists of records all with the same value for the categorical attribute, |
| return a single node with that value [7]; |
| If R is empty, then return a single node with as value the most frequent of the values of the categorical attribute that are found in records of S; [note that then there will be errors, that is, records that will be improperly classified]; |
| Let D be the attribute with largest Gain(D,S) among attributes in R; |
| Let {dj| j=1,2, .., m} be the values of attribute D; |
| Let {Sj| j=1,2, .., m} be the subsets of S consisting respectively of records with value dj for attribute D; Return a tree with root labeled D and arcs labeled d1, d2, .., dm going respectively to the trees ID3(R-{D}, C, S1), |
| ID3(R-{D}, C, S2), .., ID3(R-{D}, C, Sm); |
| End ID3[3]; |
III. DATASETS |
| We are taking the binary dataset in this for soil erection problem from the repositories and apply it on the matlab. In the matlab we implement different- different classification algorithms and predict a useful result that will be very helpful for the new users and new researchers. |
| DATA SETS IN OUR CODE |
 |
 |
IV. RESULT |
| The results show the concept of the multi grouping so that we can check on the things over the accuracy. Now for this thing to be implemented, first of all we need random attributes. We have taken here 4 random attributes namely a, b, c and d. |
 |
V. CONCLUSION |
| Applying data mining classification algorithms on the soil erection problem .We conclude that how the accuracy and privacy effected on the different data sets using new group. In which we implemented the ID3 ALGORITHM and will the check the accuracy terms with the C MEAN algorithm, if we increase the privacy level then accuracy decreases. The results shows that soil is belonging to which group and the amount of nutrients present in the soil. |
References |
|