Clustering Uncertain Data Using Voronoi Diagrams and R-Tree Index

Abstract

Clustering uncertain objects has been a topic for research. In this paper the process of clustering uncertain objects and the usage of PDFs (Probability Density Functions) to describe their locations is considered. UKmeans algorithm is not efficient in handling uncertain objects. This paper demonstrates it. The reason for its inefficiency can be traced back to the fact that it computes EDs (Expected Distances) between cluster representatives and objects. It performs numerical integrations for computing EDs which are expensive. In this paper the concept of Voronoi diagrams is proposed to reduce number of ED calculations. When compared with previous bounding-box-based technique, this is more effective and analytically proven. Furthermore this paper proposes building an R-tree index in order to organize uncertain objects. This can effectively reduce overheads pertaining to pruning. The experiments revealed that the techniques used in this paper are additive. Moreover, when used in combination they outperformed earlier methods.

INTRODUCTION

In many real time applications clustering is widely used. K- Means like algorithms are efficient in clustering. However, all these algorithms deal with objects whose distance is well known. The goal of this paper is to work with uncertain database where distance between objects is dynamic and not known. Grouping objects into clusters will make the applications effective. For instance mobile devices can be grouped and one of the devices can be elected as leader for better coordination. It can involve in certain application specific operations like collecting other nodes information etc. This will improve energy conservation and bandwidth utilization.

In this paper, the problem of clustering is considered for uncertain objects whose locations are specified by uncertainty regions over which arbitrary probability density functions are defined. In this paper, we concentrate on the problem of clustering objects with location uncertainty. Rather than a single point in space, an object is represented by a pdf overthe space Rm being studied. We assume that each object isconfined in a finite region so that the probability density outside the region is zero. Each object can thus be boundedby a finite bounding box.

1.1 Contribution of this Paper

Introduction of new pruning techniques is an important contribution of this paper.The new set of pruning techniques for the UK-means algorithm are based on Voronoi diagrams. These techniques take spatial relationship among clustering representatives into consideration. The techniques based on Voronoi diagrams are more effective than bounding box-based technique. Patrial ED calculation that reduces 95 percent of calculations is another method introduced in this paper. A boosting technique based on R-tree index is also introduced in order to reduce execution time. An important observation is that the two techniques have different goals. For instance the techniques pertaining to Voronoi-diagram reduce amount of ED calculations at the expense of some pruning cost. The pruning cost is further reduced by R-tree based boost

II. RELATED WORKS

Data uncertainity has been under research. It is classified into two types. They are existential uncertainity and value uncertainty. Existential uncertainty refers to whether an object exists or not. For instance existence of a data tuple which is associated with probability that represents confidence of its presence. Value uncertainity refers to the fact that a tuple exists but its value is now known correctly. This paper studies problem of clustering objects with value uncertainty. ―Imprecise query processing‖ is a well- studied topic on this problem. Some examples in this area are indexing structures imprecise location dependent query processing and nearest neighbor query processing. Cluster analysis can be used to identify model parameters to minimize an objective function and to identify high density connected regions. The EM (Expectation – Maximization) framework can be used to handle data uncertainty. Kmeans algorithm was extended into UK-means algorithm for clustering [2].

CK-means was introduced to improve the efficiency of UK- means with the help of efficient computing of EDs. Many pruning techniques such as min-max-dist pruning have been introduced for reducing overhead in ED calculations.

However the pruning techniques proposed in this paper are In addition to studies in partition-based uncertain data clustering [1] [4] other directions for the same purpose include density based clustering density-based classification and frequent item set mining. Two well known algorithms for density based clustering such as OPTICS and DBSCAN are extended to handle uncertain data. The extended algorithms are FOPTICS and FDBSCAN respectively. DBSCAN defines core objects and reachability while FDSCAN they are redefined to handle uncertain data. In order to cluster uncertain data FOPTICS takes similar approach of using probabilities.

Fuzzy clustering is also similar to clustering uncertain data. In such technique fuzzy subset of objects are used with degree of belongingness‖ for each object. Fuzzy C-means is widely used for fuzzy clustering. The technique followed in this paper uses only hard clustering. This means that each object belongs to only one cluster. In computational geometry, Voronoi diagram [3] [5]is a well-known structure. It has been applied for clustering in this paper. Voronoi trees [3] have been proposed to answer Reverse Nearest Neighbor (RNN) queries. More advanced pruning techniques are used in TPL algorithms.

A tree that resembles a B+ tree and is self balancing tree is known as R-tree. It is meant for indexing multidimensional data points for easy searching with k- nearest (kNN) queries. R-trees are also available with RDBMS like MY SQL, Oracle, SQLite etc. R-tree can record MBR (Minimum Bounding Rectangle) for each group for answering spatial queries. This paper makes use of R-tree for optimization of query processing.

III. DEFINITIONS

The equation of PDF is as given below. fi(x) ≥ 0 x€ Rm, more powerful than those pruning techniques. For clustering uncertain data using k-center, k-median and k-∫ xε R m fi(x) dx = 1.

means [2], guaranteed approximation algorithms have been proposed Equation for ED calculation.

To calculate the sum of squared expected distance the following equation is used. [ED(oi,ch(i))]2

IV. ALGORITHMS

4.1 UK-Means

It is an improved form of K-means. The algorithm’s pseudo code is as given below.

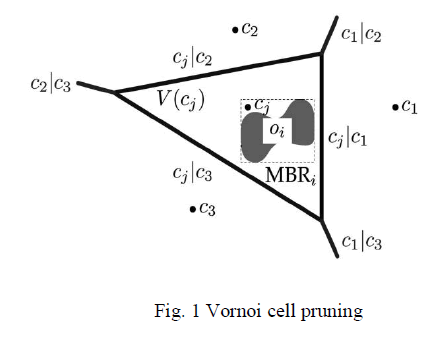
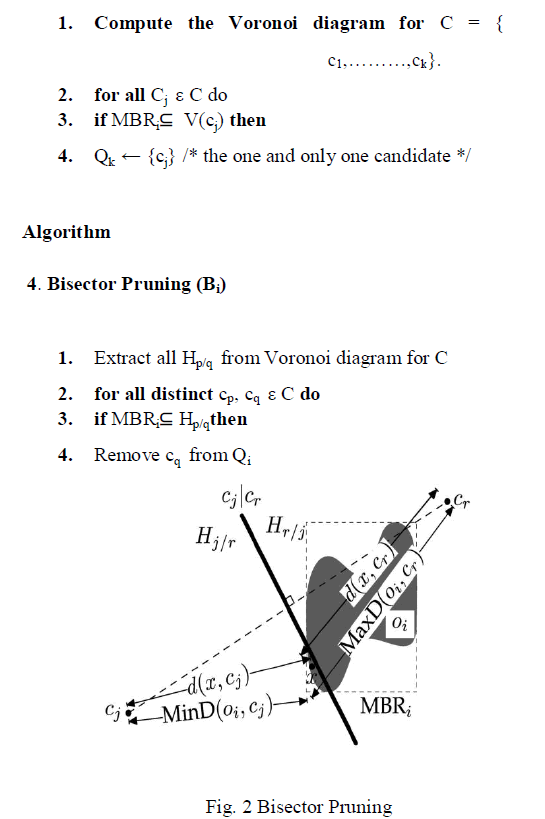
4.3 Pruning with Voronoi Diagram

The pruning techniques based on Voronoi diagram are of two types. They are Voronoi cell pruning and Voronoi bi-sector pruning. The pseudo code for the both are as given below.

Algorithm

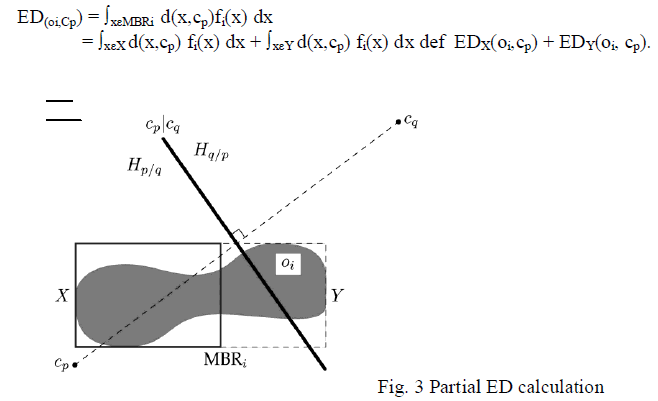
4.4 Partial ED Computation

This is part of pruning technique such as bi-sector pruning in which ED calculation is not done to enter object set. Unlike other techniques used previously, this paper presents ED calculation reduces 95 percent of unnecessary computations. The equation for ED calculation is as given below.

4.5 Indexing and Uncertain Objects

The pruning concept reduced 95 percent pruning overhead. However, the pruning cost has become significant. This means that the pruning is achieved at the cost of overhead. Now this pruning cost has to be reduced. To achieve it, this paper proposes R-trees that can be effectively used to reduce the cost of pruning. The following algorithm helps in using R-tree to reduce execution time.

Algorithm

V. PROCESS INTERNAL NODE

Hybrid Algorithms

Pruning techniques such as Voronoi cell pruning, bi- sector pruning etc. can be combined to achieve more effective results. However, the following points are to be observed.

Do not combine MinMax-BB with Voronoidiagram-based methods. This is because we haveshown that Bisector pruning is strictly stronger thanMinMax-BB pruning.

Do not consider VD pruning when an R-treeindex is used. Under VD pruning, a Voronoidiagram is constructed on the set of all clusterrepresentatives C. Let us call this diagram the―globalVoronoi diagram.‖ Assume that we use an R-treeindex.

VI. CONCLUSIONS

From the work done and the results of experiments analyzed the following conclusions are made.

• PDFs are used to represent locations of uncertain objects while clustering them.

• It is found that UK-Means algorithm is not effective.

• It is found that MinMax-BB and CS have improvements over UM-Means. However, they do not consider spatial relationship among cluster representatives.

• New techniques are derived from Voronoi diagrams for pruning. They are Voronoi cell pruning and bisector pruning. Bisector is stronger than MinMax-BB. More than 95 percent of ED calculations are pruned in the new techniques.

• Spatial pruning is derived from R-tree index for further improvement.

• Results revealed that computational overhead is less and improvement in performance is achieved with effective pruning methods.

References

1. H. Hamdan and G. Govaert, ―Mixture Model Clustering ofUncertain Data‖ Proc. 14th IEEE Int’l Conf. Fuzzy Systems, pp. 879-884, May 2005.
2. S.D. Lee, B. Kao, and R. Cheng, ―Reducing UK-Means to KMeans,‖Proc. First Workshop Data Mining of Uncertain Data(DUNE), in Conjunction with the Seventh IEEE Int’l Conf. Data mining(ICDM), Oct.2007.
3. F.K.H.A. Dehne and H. Noltemeier, ―Voronoi Treesand ClusteringProblems,‖ Information Systems, vol. 12, no.2, pp. 171-175,1987.
4. H.-P. Kriegel and M. Pfeifle, ―Density-Based Clustering ofUncertain Data,‖ Proc. Int’l Conf. Knowledge Discovery and DataMining (KDD), pp. 672-677, Aug. 2005.
5. F. Aurenhammer, ―Voronoi Diagrams—A Survey of a FundamentalGeometric Data Structure,‖ ACM Computing Surveys,vol. 23, no. 3, pp. 345-405, 1991.