Combined Effects of Radiation and Hall Current on MHD Flow Past an Exponentially Accelerated Vertical Plate in the Presence of Rotation

Abstract

The theoretical solution of Magneto Hydro Dynamic flow past an exponentially accelerated vertical plate in the presence of Hall current and thermal radiation effect relative to a rotating fluid with uniform temperature and mass diffusion is presented. The dimensionless equations are solved using Laplace method. The temperature and concentration fields, axial and transverse velocity profiles are studied for different parameters such as Schmidt number, Prandtl number, Hall parameter (m), Hartmann number (M), Rotation parameter (Ω),thermal Grashof number (Gr) and mass Grashof number (Gc). The effects of all these parameters on the axial and transverse velocity profiles are shown graphically.

Keywords

Hall Effect, Radiation, Rotation, exponentially, heat and mass transfer.

INTRODUCTION

Combined effect of heat and mass transfer in the presence of thermal radiation has been studied for its important application in Nuclear power plants, gas turbines and various propulsion devices for aircraft, remote sensing for astronomy and space exploration and many other engineering fields.

The rotating flow of an electrically conducting fluid in the presence of magnetic field is encountered in cosmical, geophysical fluid dynamics; also in solar physics, involved in the sunspot development, the solar cycle and the structure of rotating magnetic stars.

The study of MHD Viscous flows with Hall currents has important engineering applications in problems of MHD Generators, Hall Accelerators as well as in Flight Magneto Hydrodynamics.

II. RELATED WORK

Effects of Hall current and free stream velocity on the magneto hydrodynamic flow over a moving plate in a rotating fluid was studied by Takhar et.al.[5]. Hayat and abbas [1] studied the fluctuating rotating flow of a secondgrade fluid past a porous plate with variable suction and Hall current. Magua,A.N and Mutua,N.M [2] studied the Hall current effects on Free convection flow and mass transfer past semi-infinite vertical flat plate. Hall effects and Rotational effects on MHD flow past an exponentially accelerated plate was studied by Muthucumarasamy et.al [4].

As an extension of [4], in this paper, the work has been attempted to study MHD flow with combined effects of Radiation and Hall current in an exponentially accelerated plate with respect to a rotating fluid. The aim of this paper is to find the solution of problem of MHD flow past an exponentially accelerated vertical plate with the combined effect of Hall current and radiation with uniform temperature and mass diffusion relative to a Rotating fluid.

III. MATHEMATICAL FORMULATION

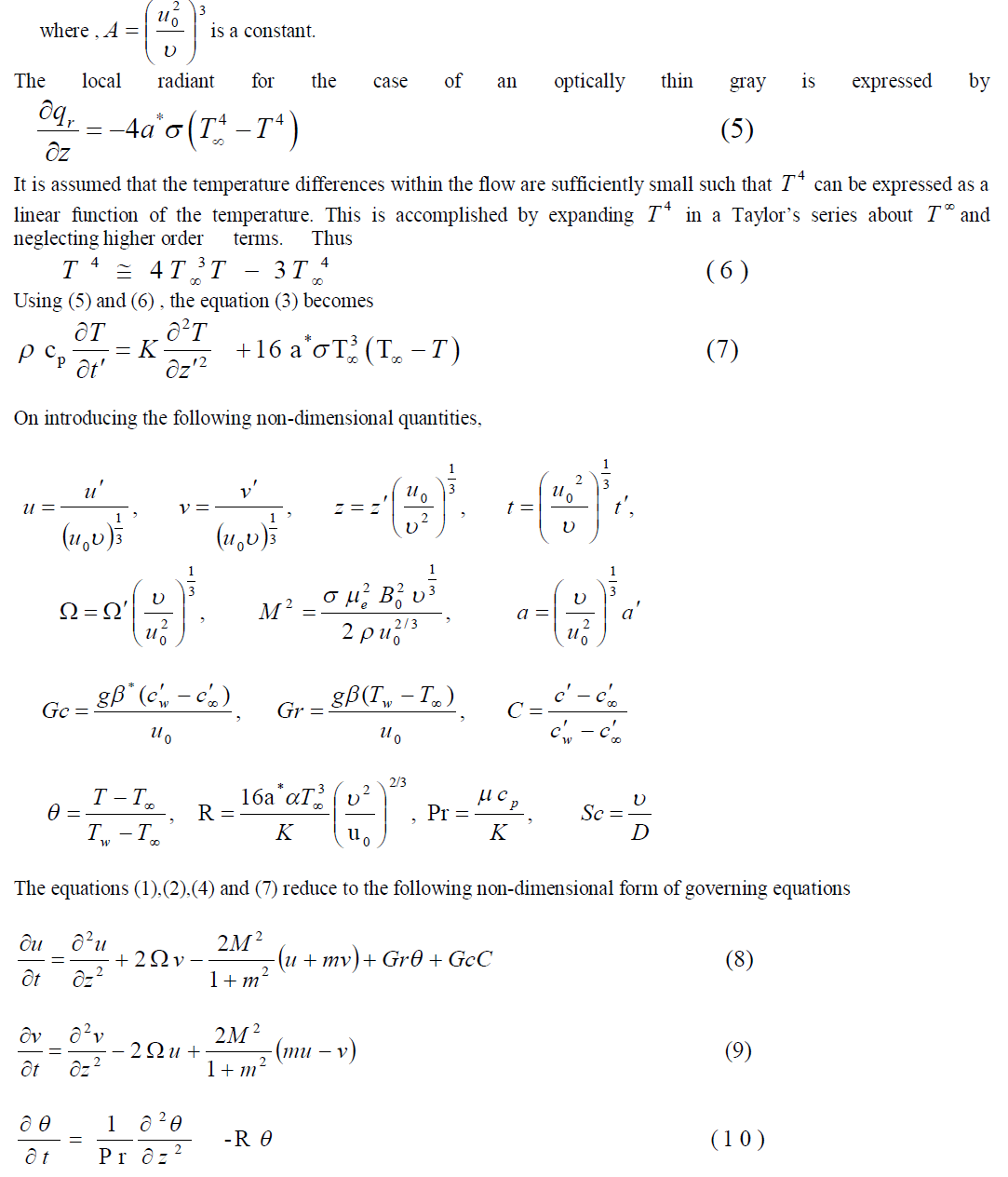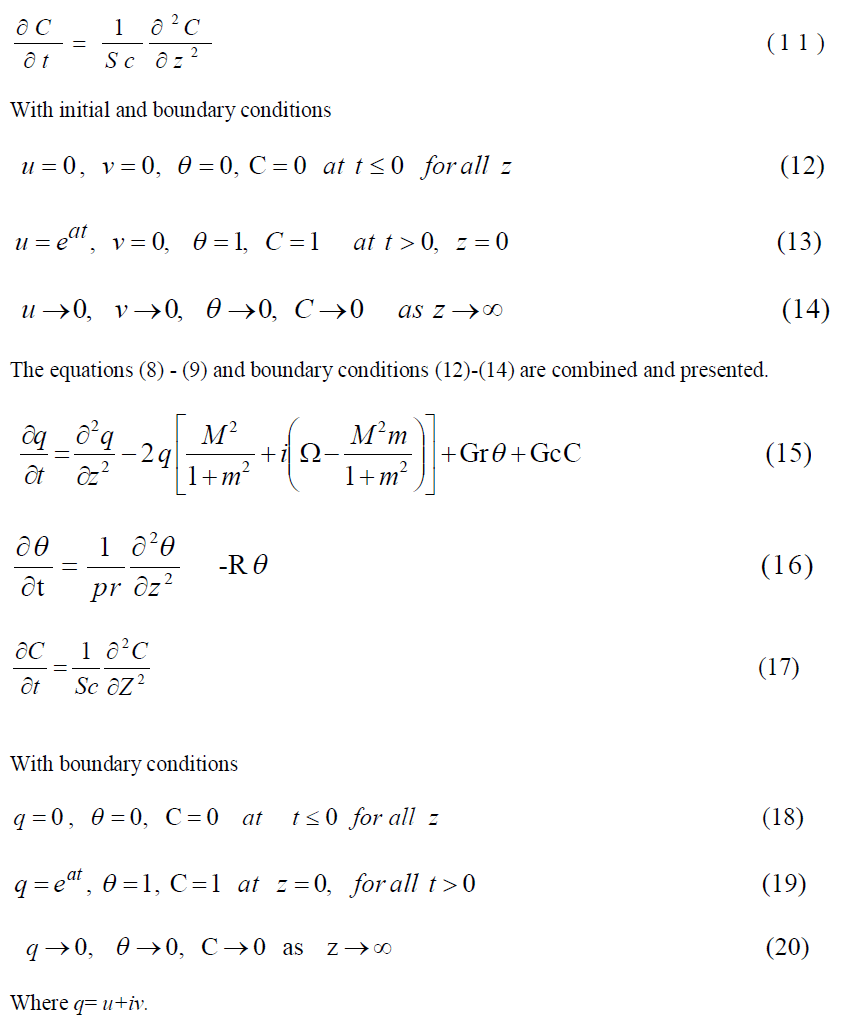IV. SOLUTION OF THE PROBLEM.

To solve the dimensionless governing equations (15) to (17), subject to the initial and boundary conditions (18)-(20) Laplace –Transform technique is used. The solutions are in terms of exponential and complementary error function:

In order to get a clear understanding of the flow field, we have separated q into real and imaginary parts to obtain axial and transverse components u and v.

V. RESULTS AND DISCUSSION

To interpret the results for a better understanding of the problem, numerical calculations are carried out for different physical parameters M,m, ,Gr,Gc,Pr and Sc. The value of Prandtl number is chosen to be 7.0 which correspnds to water.

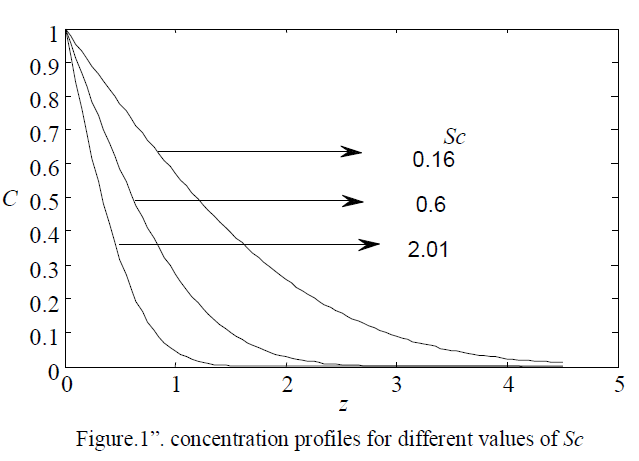
“Figure1” illustrates the effect of Schmidt number (Sc=0.16, 0.6, 2.01, when M=m=0.5, =0.1, a=2.0, t=0.2 Gr=Gc=R=5.0) on the concentration field. It is observed that, as the Schmidt number increases, the concentration of the fluid medium decreases.

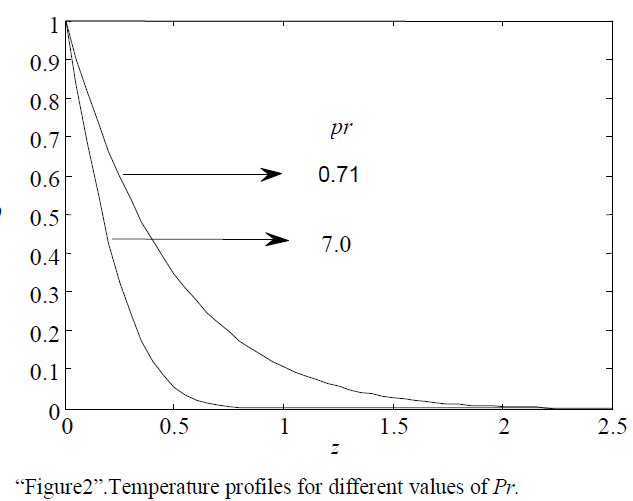
The effect of Prandtl number (Pr) on the temperature field is shown in “Figure2”. It is noticed that an increase in the prandtl number leads to a decrease in the temperature.

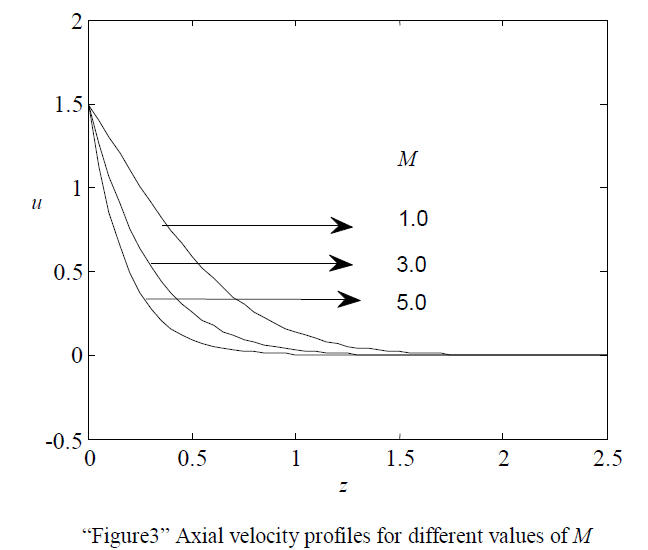
“Figure 3” illustrates that effects of the Magnetic field parameter (M=1.0, 3.0, 5.0, when Gr = Gc=R=5.0, m=0.5, a=2.0, t=0.2) on axial velocity. It is observed that, the axial velocity decreases with the increasing value of M. This agrees with the expectations, since the magnetic field exerts a retarding force on the free convective flow.

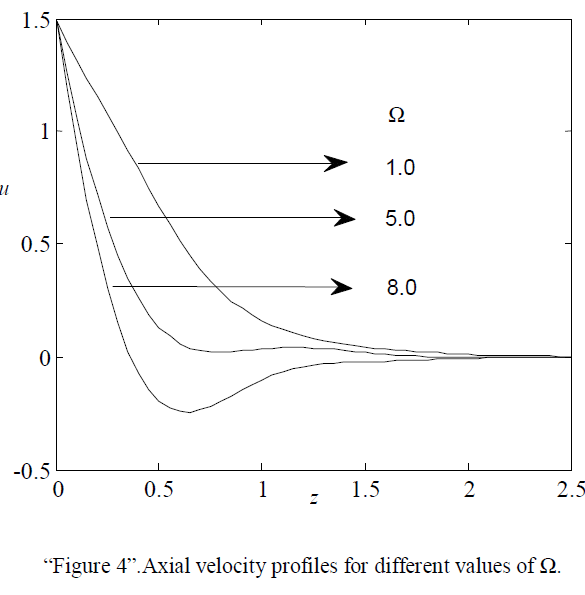
The effect of Rotation parameter on axial velocity is shown in “Figure.4.” It is observed that the velocity increase with decreasing values of  (1.0, 5.0 8.0)

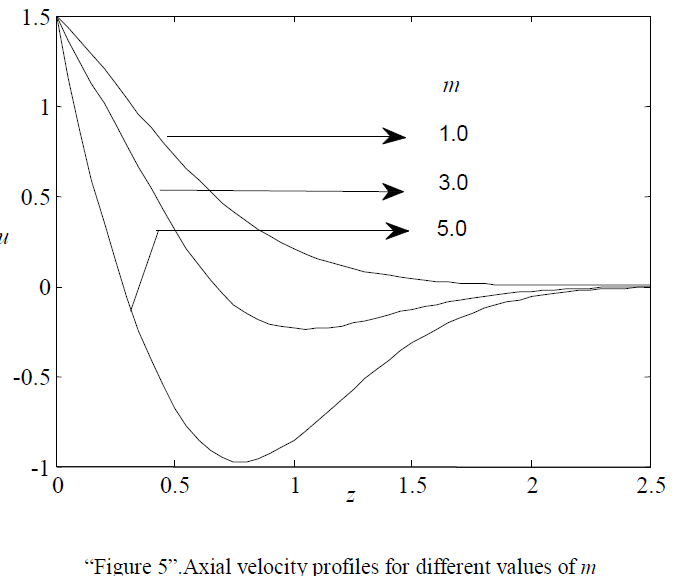
“Figure 5” demonstrates the effect of Hall parameter m on axial velocity. It has been noticed that the velocity decreases with increasing values of Hall parameter.

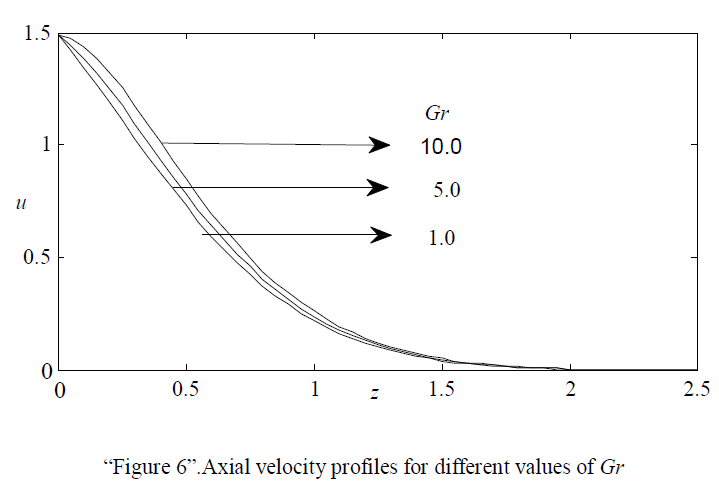
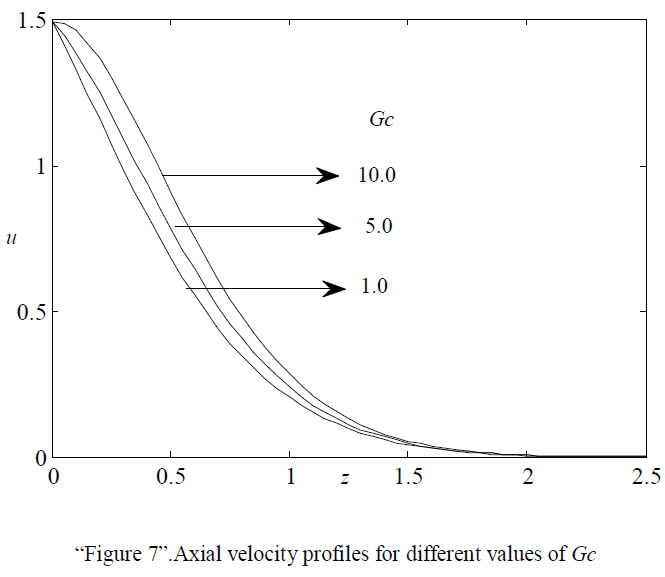
“Figures 6 and 7” respectively show the effects of thermal Grashof number Gr and mass Grashof number Gc on axial velocity. It has been noticed that the velocity increases with increasing values of both Gr and Gc, but the effects are seems to be meager.

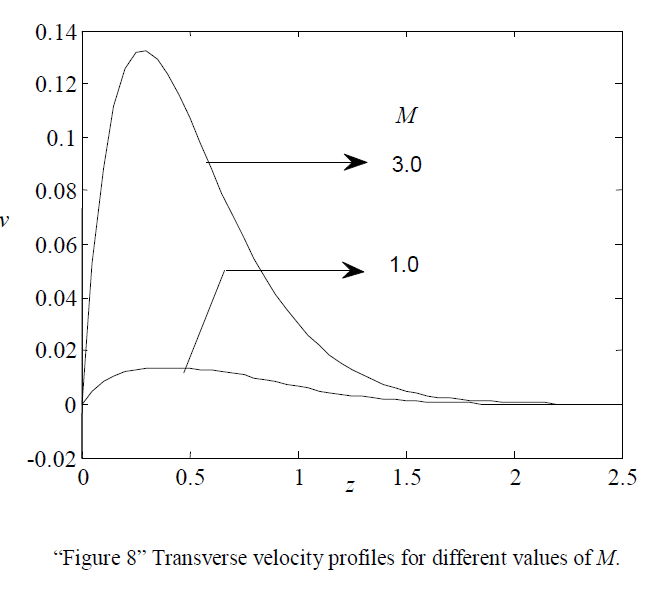
“Figure 8” illustrates the effects of Magnetic field parameter M on transverse velocity. It is observed that the transverse velocity increases with increasing values of M upto M=3.0.But it is also observed that when M>3.0, the transverse velocity starts decreasing.

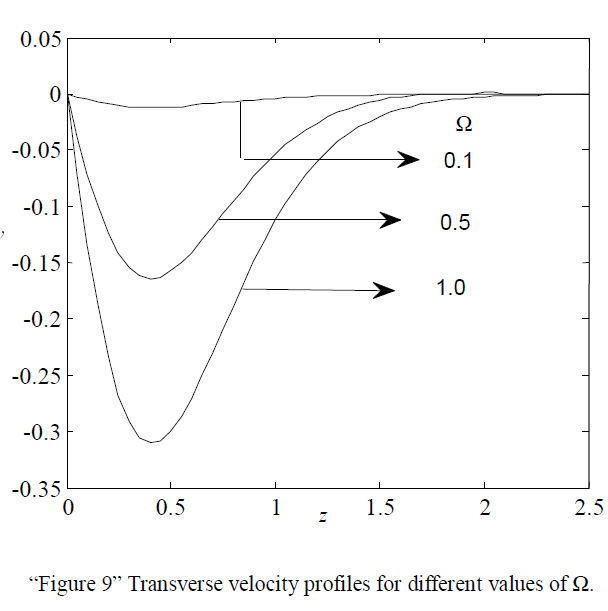
The Transverse velocity profiles for different values of Rotaion parameter  are shown in “Figure 9”. It is observed that the velocity increases with decreasing values of  .

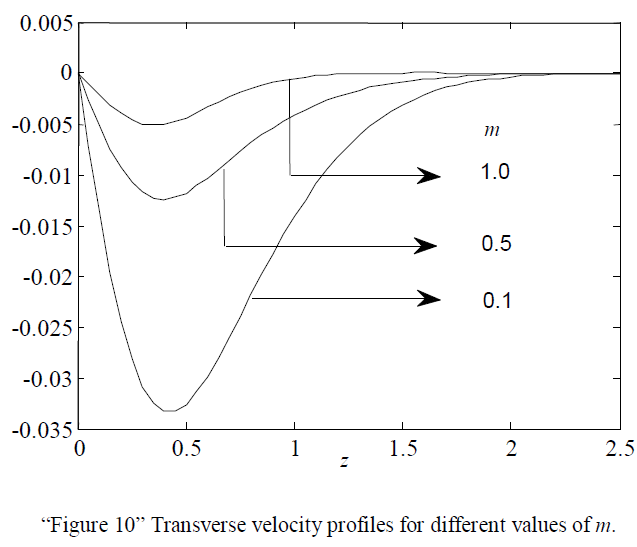
“Figure 10” shows the effect of Hall parameter m on transverse velocity. It is found that the velocity increases with increasing values of m.

“”Figure 11” demonstrates the effect of Thermal Grashof number Gr on transverse velocity. It is observed that there is an increase in velocity as there is a decrease in Gr

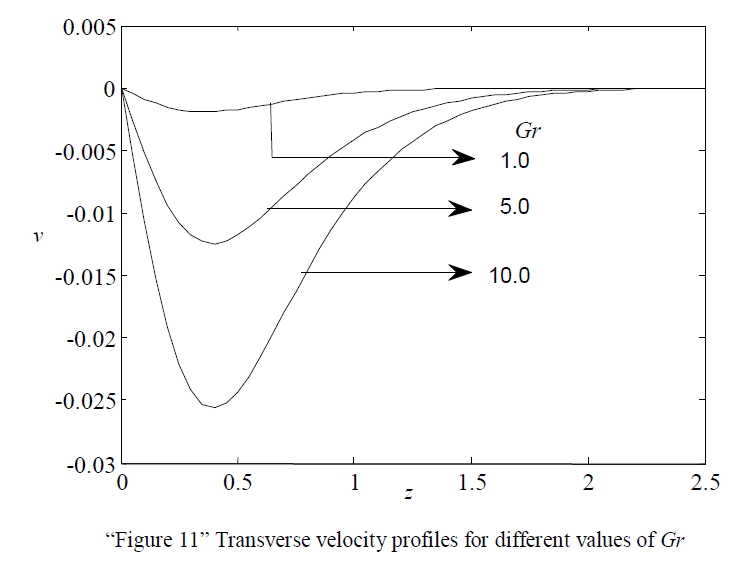The effect of Mass Grashof number on transverse velocity is shown in “Figure 12” Numerical calculations were carried out for different values of Gc namely 1.0, 5.0, 10.0. From the Figure it has been noticed that with increasing values of Gc the transverse velocity is increases. But the effect is seems to be meager.

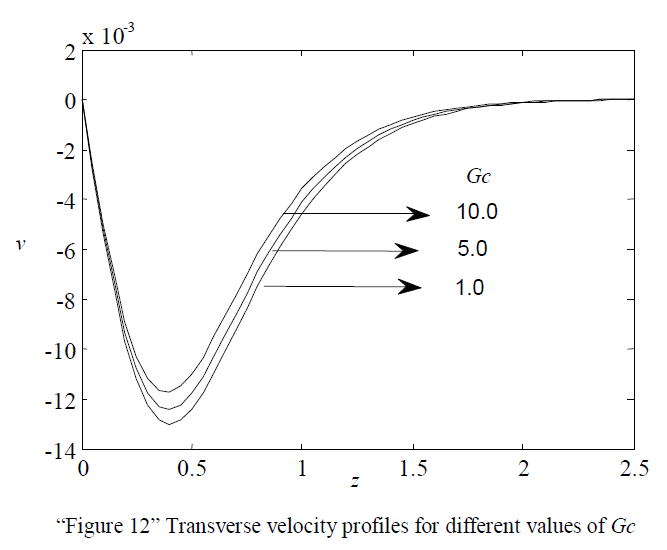VI. CONCLUSION

In this paper we have studied the effects of Hall current, Rotation effect on MHD flow through an exponentially accelerated vertical plate with uniform temperature and mass diffusion in the presence of Thermal Radiation. In the analysis of the flow the following conclusions are made.

1. The temperature of the plate decreases with increasing values of prandtl number.

2. The concentration near the plate increases with decreasing values of the Schmidt number.

3. Axial velocity increases with decreasing values of Magnetic field parameter or Rotation parameter or hall parameter.

4. Transverse velocity increases with increasing values of Magnetic parameter or Hall parameter. But the trend gets reversed in the case of Rotation parameter.

5. Axial velocity increase with increasing values of Thermal Grashof number. But the trend gets reversed in the case of transverse velocity.

6. Both the velocities increase with increasing values of Mass Grashof number.

Further work can be carried out by including the chemical reaction effect.

References

1. Hayat T., & Abbas Z, ” Effects of hall Current and Heat Transfer on the flow in a porous Medium with slip conditions” , Journal of Porous Media, Vol. 10 ,Issue No.1, pp. .35-50, 2007
2. Maguna,A.N & Mutua,N.M,” Hall current effects on Free convection flow and mass transfer past semi-infinite vertical flat plate” International Journal of mathematics and Statistics studies, Vol. 1, Issue No.4, pp.1-22, 2013
3. R.Muthucumaraswamy.,J.Maheswari.,J.Pandurangan: Study of MHD and Radiation effects on moving vertical plate with variable temperature and mass diffusion”, International review of Pure and Applied mathematics, Vol.3 ,Issue No.1, pp.95-10, 2007.
4. Muthucumaraswamy.R.,Thamizhsudar.M.,Pandurangan.J, “Hall effects and Rotational effects on MHD flow past an exponentially Accelerated Plate” Annals of Faculty Engineering, Fassicule 3, pp. -145-148 2014.
5. Takhar H.S., Chamkha A.J., and Nath G,”MHD flow over a moving plate in a rotating fluid with a magnetic field, Hall currents and free stream velocity”, International Journal of Engineering and Sciences. Vol 40,Issue No.13, Pp. 1511-1527, 2002.