Comparison of Optimistic and Pessimistic
MTTF Bounds of NIASN with ABN

Amardeep Gupta

Comparison of Optimistic and Pessimistic MTTF Bounds of NIASN with ABN

Amardeep Gupta

Head, PG, Dept of Computer Science and IT, D A V College, Amritsar, Punjab, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

The reliability can be measured in terms of MTTF i.e. Mean Time To Failure. It is defined as expected time elapsed before some source is disconnected from some destination. In this paper Optimistic and Pessimistic MTTF Bounds of proposed Multistage Interconnection Network (MIN) New Irregular Augmented Shuffle Exchange Network (NIASN) have been evaluated and compared with existing similar class of MINs Augmented Baseline Network (ABN).

Keywords

Optimistic MTTF Bound, Pessimistic MTTF Bound, Network size, Fault Tolerance.

INTRODUCTION

The optimistic and pessimistic MTTF bounds are the markers of the reliability of the MIN. These values have been calculated by considering the series and parallel connections of the components in the MIN.

LITERATURE SURVEY

Different types of Multistage Interconnection Networks have been reviewed. The studied MINs have been categorized on the basis of their design and structure. The categories which have been studied include Fault-free and Fault-Tolerant MINs. On the basis of the mathematical and analytical models, the performance measures of these MINs have also been studied. The study helps to design new MINs with better performance.

ARCHITECTURE OF NIASN

The proposed MIN has been designed by using less number of SEs in the intermediate stages and with changed connection patterns in existing MIN Irregular Augmented Shuffle Exchange Network (IASN) Sadawarti et al. (2007) The proposed MIN consists of k-1 stages (k=log2 N).The network Comprises of two identical groups of switching elements (SEs), named as G0 and G1.There are N/2 sources and N/2 destinations in each group. Both the groups are connected to the N inputs and N outputs. The inputs are connected through N multiplexers of 4:1 size, and the outputs are connected through the same number of demultiplexers of 1:2 size. The multiplexers and demultiplexers have been numbered as 0, 1, ----, N/2. In this network the switches are of size 2*2 in all the stages except the first stage where the switches are of size 3*3. The NIASN network of size N*N has (2*k) no. of switches of size 3*3 and [(2*k) +3] number of switches of size 2*2.Each source is connected to one switching element in each

group with the help of multiplexers. The multiplexers and demultiplexers have been given the numbers as 0, 1, ---, N/2- 1. The switches in the first stage have been assigned the numbers from 0, 1, ---, N/2-1, connected to each other through links called as auxiliary links. The auxiliary links are used when the SE in the next stage is busy or faulty. This makes the network more Fault-Tolerant and reliable. The switches in the middle stage have been given the number as N/2,-- ,N/2+2. Like wise the switches in the last stage are identified with the numbers from N/2+3,----,N/2+10.

OPTIMISTIC AND PESSIMISTIC MTTF BOUNDS OF NIASN AND TRIANGLE MIN

The optimistic and pessimistic MTTF bounds have been calculated by considering the series and parallel connections of the components in the MIN.

Optimistic MTTF Bound

The network is operational if the critical set of switches is operational. The critical set is the set of k SEs, each from different module such that a failure occurs if all k SEs are faulty simultaneously. The NIASN network is in operation as long as one of the two multiplexers attached to the source in any of the groups is operational. The block diagramme of this bound has been shown in Fig 2.

The functions of the stages in the network are given below

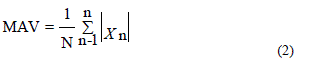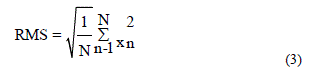The expression for optimistic Bound Reliability is

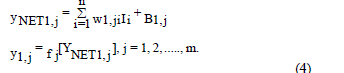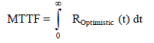The optimistic MTTF bound of the proposed NIASN network has been evaluated. Table 1 shows the values of this MTTF analysis.

The equations of Optimistic MTTF Bound of the Triangle Network are

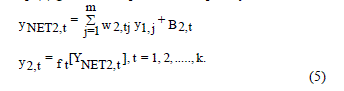The Optimistic MTTF Bound is calculated as

The Table 2 shows the values of the Optimistic MTTF Bound of Triangle Network

PESSIMISTIC MTTF BOUND

In the pessimistic MTTF Bound analysis, the input side SEs and their corresponding multiplexers are considered as a series system and failure of any component leads to the failure of all three. The functions of the stages in the network are given below

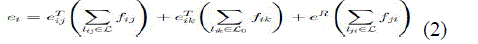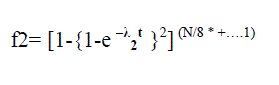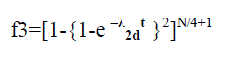The expression for pessimistic MTTF Reliability is

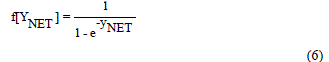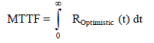The reliability block diagram for the pessimistic MTTF bound has been shown in Fig. 3.

Table 3 shows the values of the pessimistic MTTF bound of the proposed NIASN network

If two multiplexers are grouped with each switch in the source and considered as a series system, then Pessimistic MTTF Bound of Triangle MIN can be equated as below

The functions of the stages in the Triangle MIN are given below

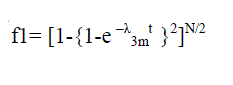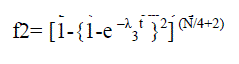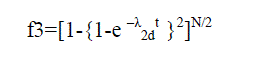The Pessimistic MTTF expression is calculated as

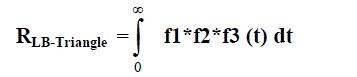Table 4, shows the values of the Pessimistic MTTF Bound of Triangle Network. Fig 1:

CONCLUSION

The NIASN MIN shows significant improvement in MTTF Bounds as compared to similar class of Network i.e. Triangle MIN. It is clear that the NIASN MIN is reliable for small size of network and is comparable to Triangle MIN as the network size grows.

Tables at a glance


Table 1	Table 2	Table 3	Table 4

Figures at a glance


Figure 1	Figure 2	Figure 3

References

Balaguruswami E, “Reliability Engineering”, Tata Mc-Graw Hill, 1989.

Das C. R. and Bhuyan L. N., “Reliability simulation of multiprocessor systems”, Proceedings International Conference on ParallelProcessing, pp. 764-771, August 1985.

Sengupta J., Bansal P. K. and Gupta A., “Permutation and Reliability Measures of Regular and Irregular MINS”, Proceedings of IEEEConference (TENCON), pp. 531-536, September 2000.

Sadawarti Harsh, Bansal P. K.,”Fault-Tolerant Irregular Augmented Shuffle Network”, Proceedings of the 2007 WSEAS InternationalConference on Computer Engineering and Applications, Gold Coast, AUSTRALIA, January 17-19, 2007.

Tripathi V. S., Tripathi C. B., Tiwari S., “Performance evaluation of a Fault-Tolerant Switch for the Next Generation Computer Networks”,Proceedings of the 12th International Conference on Parallel and Distributed Systems (ICPADS), July 2006.

BIOGRAPHY

Dr. Amardeep Gupta is Head PG Dept. of Computer Sc. and IT at D A V College, Amritsar, Punjab, India. He is B.E in Computer Sc. and Engg. He received M Tech degree from Punjabi Univ Patiala. He received his Ph. D in faculty of Engineering from Punjab Technical University, Jalandhar. He has supervised theses of 2 MCA candidates. He has got published 28 research papers in International Journals and periodicals.He has to his credit 5 research papers published in conferences. He has also presented 15 research papers in conferences. He has co-authored 10 text books. The author is member of various professional bodies. As convener he has conducted 2 National and 2 International Conferences on Computer Science. He has established computer lab at Vishveshranand Vedic Research Institute, Hoshiarpur.