School of Mathematical Sciences, Guangxi Teachers Education University,Nanning 530023, P. R. China
Received: 01/11/2015; Accepted: 04/11/2015; Published: 16/11/2015
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
In the paper, the stochastic Kaldor-Kalecki model of business cycle with noise is investigated. By analyzing the Lyapunov exponent, invariant measure and singular boundary theory, some new criteria ensuring stochastic stability, P-bifurcation and pitchfork bifurcation for stochastic Kaldor-Kalecki model are obtained, respectively. Numerical simulation results are given to support the theoretical predictions.
Kaldor [1] proposed a ordinary differential system to model business cycle, in which the gross investment depends on the level of output and capital stock. Thereafter, this model was often discussed, see [1-11] and references there in. The Kalecki business model [5] was a few years earlier than the Kaldor one. Kalecki assumed that the saved part of profit is invested and the capital growth is due to past investment decisions. There is a gestation period or a time lag, after which capital equipment is available for production. In 1999, Krawiec and Szydlowski [6] have formulated the Kaldor-Kalecki business cycle model based on the multiplier dynamics which is the core of both the Kaldor (after Keynes) and Kalecki approach. However, they employed Kaleckis approach to investment and of a time lag between investment decisions and implementation. The model is as following form:
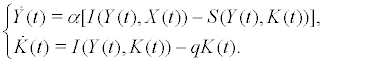 (1)
(1)
Clearly, introducing noise and time delays into the business model is more reasonable. On the model, Krawiec and Szydlowski [7-11] have studied the stability and existence of Hopf bifurcations by analyzing the characteristic equation associated with the model, the method cannot be applied to the stochastic model. In general, stochastic delay-differential equations exhibit much more complicated dynamics than the responding ordinary differential equations since a time delay or noise could cause the change of stability of an equilibrium, and hence Hopf bifurcation occurs.
It is interested to investigate the noise or time delay how to affect the dynamics of a system, and it is important to determine the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions when a Hopf bifurcation occurs. Taking these factors into account we introduce randomness into the model by replacing the parameters β and q 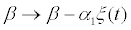 and
and 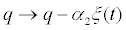 This is only a first step in introducing stochasticity into the model. Ideally we would also like to introduce stochastic environmental variation into the other parameters such as the transmission coefficient α and γ , the total rate of production of healthy cells per unit time, but to do this would make the analysis much too difficult. In this paper, we consider the Kaldor-Kalecki model of business cycle with noise as following
This is only a first step in introducing stochasticity into the model. Ideally we would also like to introduce stochastic environmental variation into the other parameters such as the transmission coefficient α and γ , the total rate of production of healthy cells per unit time, but to do this would make the analysis much too difficult. In this paper, we consider the Kaldor-Kalecki model of business cycle with noise as following
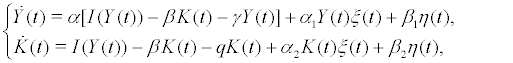
where
• Y is the gross product and K the capital product of the business cycle;
• 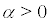 measure the reaction of the system to the difference between investment and saving;
measure the reaction of the system to the difference between investment and saving;
• q∈(0,1) is the depreciation rate of capital stock;
•  are investment and saving function of Y and K, respectively;
are investment and saving function of Y and K, respectively;
• 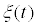 is the multiplicative random excitation and η (t) is the external random excitation directly(namely additive random).ξ (t) and η (t) are independent, in possession of zero mean value and standard variance Gauss white noises. i.e.
is the multiplicative random excitation and η (t) is the external random excitation directly(namely additive random).ξ (t) and η (t) are independent, in possession of zero mean value and standard variance Gauss white noises. i.e.
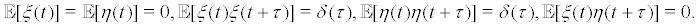 And
And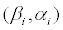 is the intensities of the white nois
is the intensities of the white nois
The theory of random dynamical system provides a very powerful mathematical tool for understanding the limiting behavior of stochastic system. Recently, it has been applied to economics and finance to help in understanding the stochastic nature of financial model with random perturbations [12-17]. In particular, the study of the limiting distributing of various stochastic models in economics and finance give a good description of stationary business cycle. There seems to have been no application of it to Kaldor-Kalecki model of business cycle. Our purpose in this paper is to investigate the stochastic bifurcation and stability for (2) by applying the singular boundary theory, Lyapunov exponent and the invariant measure theory, the direction of the Hopf bifurcation and the stability of bifurcating periodic solutions are also determined. We also give numerical example to simulate the results found by using the Matlab and Mathematica software .
The structure of the paper is as follows. In Section 2, we fist outline the extended model of Kaldor-Kalecki model of business cycle. In Section 3 and 4, the stochastic dynamical behavior is analyzed from the viewpoint of stationary measures and invariant measure respectively. The paper is then concluded in Section 5.
In the section, we present some preliminary results to be used in a subsequent section to establish the stochastic stability and stochastic bifurcation. Before proving the main theorem we give some lemmas and definitions.
Throughout the rest of this paper, we assume that α ,β > 0,q,γ ∈(0,1) and that I (s) is C4 C4. Let (Y*,K* ) be an equilibrium point Let (Y*,K* ) be an equilibrium point of system (2),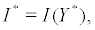 and
and 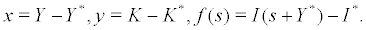 Then system (2) can be transformed as
Then system (2) can be transformed as
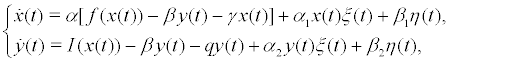 (3)
(3)
Let the Taylor expansion of f at 0. Then we can rewrite (3) as the following equivalent system
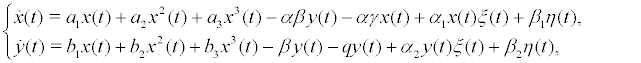 (4)
(4)
where, 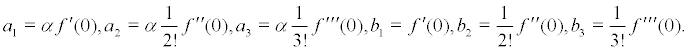
Let 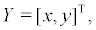 then by substituting the corresponding variables in Eq. (4)
then by substituting the corresponding variables in Eq. (4)
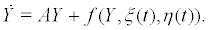
So discussing the stability of system (2) at equilibrium point Q is equivalent to discussing the stability of system (6) at equilibrium point O(0,0).
Let
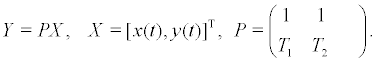
where
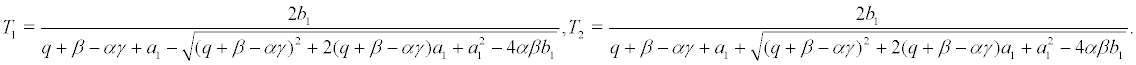
Then by substituting the corresponding variable in the equations, we obtain
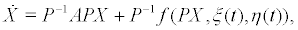
i.e.
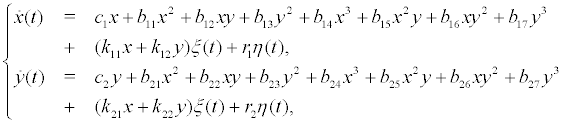
where the coefficient are denoted as following:
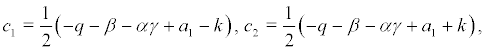
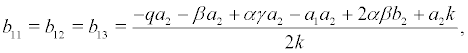
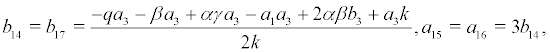
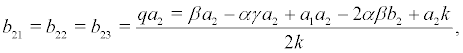
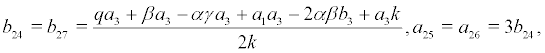
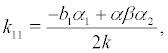
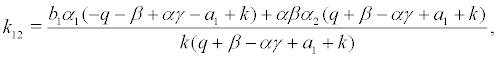
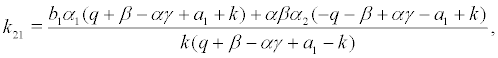
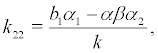
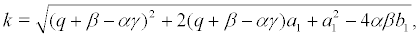
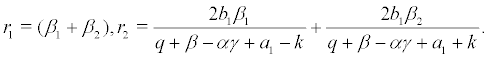
Set the coordinate transformation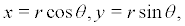 and by substituting the variable in (6), we obtain
and by substituting the variable in (6), we obtain
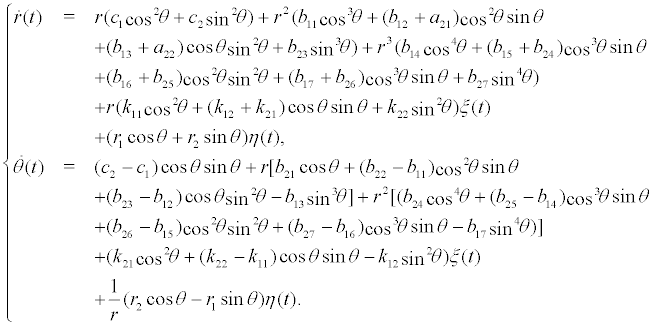
It is difficult to calculate the exact solution for system (7) today. According to the Khasminskii limit theorem, when the intensities of the white noises 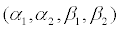 is small enough, the response process
is small enough, the response process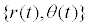 weakly converged to the two-dimensional Markov diffusion process [18-20]. Through the stochastic averaging method, we obtained the It
weakly converged to the two-dimensional Markov diffusion process [18-20]. Through the stochastic averaging method, we obtained the It stochastic differential equation
stochastic differential equation  the process satisfied
the process satisfied
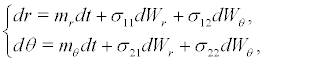 (8)
(8)
where 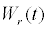 and
and 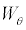 are the independent and standard Wiener processes. As for the two-dimensional diffusion process, it is necessary to calculate its two-dimensional transition probability density. There is no general and right method for the calculation. As for the concrete system, we could finish the calculation with some special techniques
are the independent and standard Wiener processes. As for the two-dimensional diffusion process, it is necessary to calculate its two-dimensional transition probability density. There is no general and right method for the calculation. As for the concrete system, we could finish the calculation with some special techniques
Under the condition 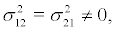 system(8) is rewritten as follows
system(8) is rewritten as follows
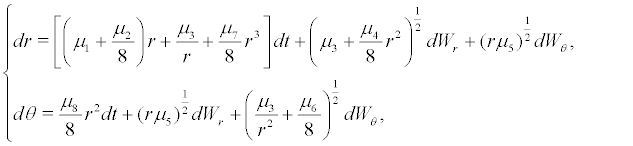 (9)
(9)
where
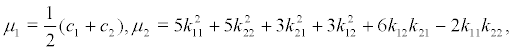
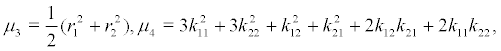
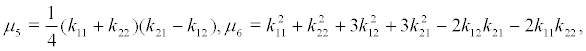
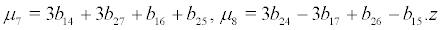
From the diffusion matrix, we can find that the averaging amplitude r(t) is a one-dimensional Markov diffusing process when
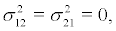 i.e
i.e 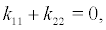 or
or 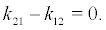 Thus we have the equation as following
Thus we have the equation as following
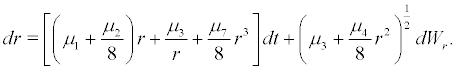 (10)
(10)
This is an efficient method to obtain the critical point of stochastic bifurcation through analyzing the change of stability of the averaging amplitude r(t) in the meaning of probability.
In order to detect the local stochastic stability of the stochastic averaging system, the method that we often used is to calculate the maximum Lyapunov exponent.
Theorem 3.1 If 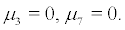
(i) When 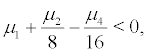 then the stochastic system (2) is stochastically stable.
then the stochastic system (2) is stochastically stable.
(ii) When 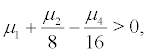 then the stochastic system (2) is stochastically unstable.
then the stochastic system (2) is stochastically unstable.
Proof. When 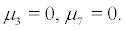 Then system (10) becomes
Then system (10) becomes
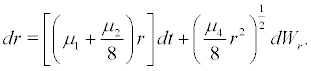 (11)
(11)
Using the solution of linear Itô stochastic differential equation, we obtain the solution of system (11) as follow
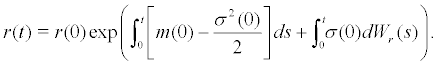 (12)
(12)
where
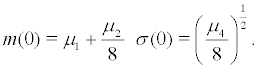
Using the theorem of qusi-non-integrable Hamiltonian system, here we define a new norm: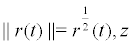 thus, the approximation of Lyapunov exponent of the linear Itô stochastic differential equation is:
thus, the approximation of Lyapunov exponent of the linear Itô stochastic differential equation is:
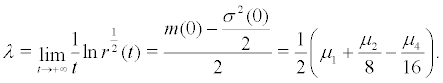
Thus we have:
When 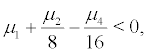 that is λ < 0 , thus the trivial solution of the linear Itô stochastic differential equation r = 0 is stable in the meaning of probability, i.e. the stochastic system is stable at the equilibrium point Q . In addition the linear Itô stochastic differential equation have robustness , i.e. the trivial solution r = 0 of the nonlinear Itô stochastic differential equation (10) is stable in the meaning of probability. This demonstrates that the deterministic system is steady at its equilibrium point, it may also be steady in the meaning of probability at its equilibrium point under random excitations.
that is λ < 0 , thus the trivial solution of the linear Itô stochastic differential equation r = 0 is stable in the meaning of probability, i.e. the stochastic system is stable at the equilibrium point Q . In addition the linear Itô stochastic differential equation have robustness , i.e. the trivial solution r = 0 of the nonlinear Itô stochastic differential equation (10) is stable in the meaning of probability. This demonstrates that the deterministic system is steady at its equilibrium point, it may also be steady in the meaning of probability at its equilibrium point under random excitations.
When 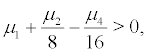 that is λ > 0. Thus the trivial solution of the linear Itô stochastic differential equation r = 0 is unstable in the meaning of probability, i.e. the stochastic system is unstable at the equilibrium point Q . This demonstrates that although the deterministic system is steady at its equilibrium point, the stochastic system may be unstable in the meaning of probability at its equilibrium under random excitations.
that is λ > 0. Thus the trivial solution of the linear Itô stochastic differential equation r = 0 is unstable in the meaning of probability, i.e. the stochastic system is unstable at the equilibrium point Q . This demonstrates that although the deterministic system is steady at its equilibrium point, the stochastic system may be unstable in the meaning of probability at its equilibrium under random excitations.
When 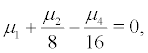 that is λ = 0. Whether
that is λ = 0. Whether 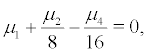 or not can be regarded as the critical condition of bifurcation at the equilibrium point. And whether the Hopf bifurcation could occur or not are what we will discuss in the next section.
or not can be regarded as the critical condition of bifurcation at the equilibrium point. And whether the Hopf bifurcation could occur or not are what we will discuss in the next section.
The max Lyapunov exponent based on Oseledec multiplicative ergodic theory can only be used to judge the local stability, here we judge the global stability by the singular boundary theory. In the section, according to the singular boundary theory, we will obtain stability of the stochastic averaging system.
Theorem 3.2 Let 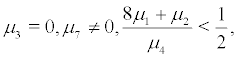 and
and 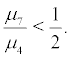 Then the stochastic system (2) is stochastically stable.
Then the stochastic system (2) is stochastically stable.
Proof. When 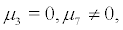 the system (10) can be rewritten as follows
the system (10) can be rewritten as follows
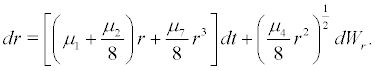 (13)
(13)
Thus r = 0 is the first kind of singular boundary of system (13). When 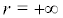 we can find
we can find 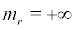 thus
thus 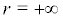 is the second kind of singular boundary of system (13).
is the second kind of singular boundary of system (13).
According to the singular boundary theory, we can calculate the diffusion exponent, drifting exponent and characteristic value of boundary r = 0 and the results are as follows:
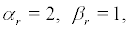
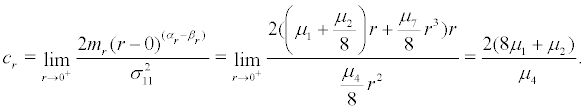 (14)
(14)
So
if 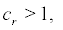 i.e.
i.e.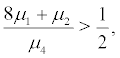 the boundary r = 0 is exclusively natural.
the boundary r = 0 is exclusively natural.
if 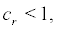 i.e
i.e 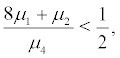 the boundary r = 0 is attractively natural.
the boundary r = 0 is attractively natural.
If 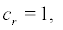 i.e.
i.e.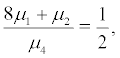 the boundary r = 0 is strictly natural.
the boundary r = 0 is strictly natural.
We can also calculate the diffusion exponent, drifting exponent and characteristic value of boundary r = +∞ , and the results are as follows:
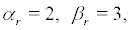
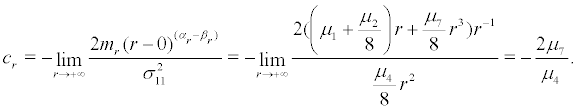 (15)
(15)
So
if 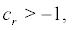 i.e.
i.e. 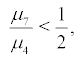 the boundaryis
the boundaryis 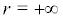 exclusively natural.
exclusively natural.
if 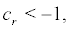 i.e.
i.e.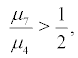 the boundary
the boundary 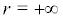 is attractively natural
is attractively natural
If 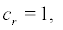 i.e.
i.e.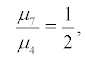 the boundary
the boundary 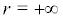 is strictly natural
is strictly natural
As we know, if the singular boundary r = 0 is attractively natural boundary and 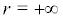 is entrance boundary, this situation is all the solve curves enter the inner system from the right boundary and is attracted by the left boundary, the equilibrium point is global stable.
is entrance boundary, this situation is all the solve curves enter the inner system from the right boundary and is attracted by the left boundary, the equilibrium point is global stable.
From the analysis above, we can draw a conclusion that the equilibrium point is global stable when the singular boundary r = 0 is attractively natural boundary and 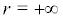 is entrance boundary. Combine the condition of local stability, the equilibrium
is entrance boundary. Combine the condition of local stability, the equilibrium
point r = 0 is stable when 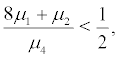 and
and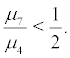
Theorem 3.3 Let 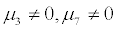 Then the stochastic system (2) is not stochastically stable.
Then the stochastic system (2) is not stochastically stable.
Proof. When 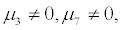 ≠ 0, the system (10) can be rewritten as follows:
≠ 0, the system (10) can be rewritten as follows:
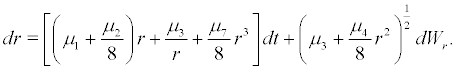 (16)
(16)
One can find 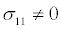 at r = 0, so r = 0 is a nonsingular boundary of system (16). Through some calculations we can find that r = 0 is a regular boundary(reachable). The other result is
at r = 0, so r = 0 is a nonsingular boundary of system (16). Through some calculations we can find that r = 0 is a regular boundary(reachable). The other result is 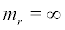 when
when 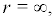 so
so 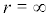 is second singular boundary of (16). The details are presented as follows:
is second singular boundary of (16). The details are presented as follows:
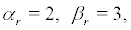
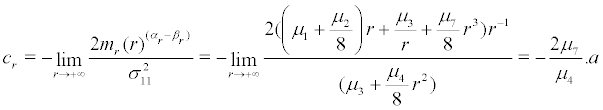 (17)
(17)
So
if 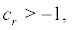 i.e.
i.e.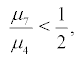 the boundary
the boundary 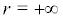 is exclusively natural.
is exclusively natural.
If 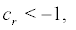 i.e.
i.e. 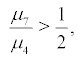 the boundary
the boundary 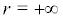 is attractively natural.
is attractively natural.
If 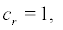 ,i.e.
,i.e. 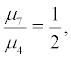 the boundary r = 0 is strictly natural.
the boundary r = 0 is strictly natural.
As we know, if the singular boundary r = 0 is attractively natural boundary and r = +∞ is entrance boundary, this situation is all the solve curves enter the inner system from the right boundary and is attracted by the left boundary, the equilibrium point is global stable.:
From the analysis above, we can draw a conclusion that the equilibrium point is global stable when the singular boundary r = 0 is attractively natural boundary and r = +∞ is entrance boundary. Combine the condition of local stability, the equilibrium point r = 0 is stable when 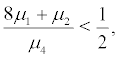 and
and 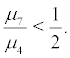
Theorem 3.3 Let 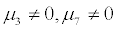 . Then the stochastic system (2) is not stochastically stable.
. Then the stochastic system (2) is not stochastically stable.
Proof. When 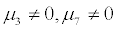 , the system (10) can be rewritten as follows:
, the system (10) can be rewritten as follows:
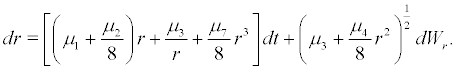 (16)
(16)
One can find 11 σ ≠ 0 at r = 0, so r = 0 is a nonsingular boundary of system (16). Through some calculations we can find that r = 0 is a regular boundary(reachable). The other result is = r m ∞ when r = ∞, so r = ∞ is second singular boundary of (16). The details are presented as follows:
α2=2,βr=3,
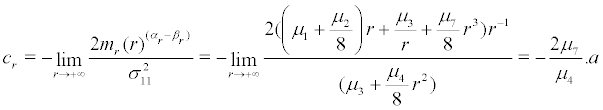 (17)
(17)
So
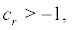 i.e.
i.e. 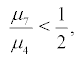 the boundary r = +∞ is exclusively natural.
the boundary r = +∞ is exclusively natural.
If 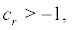 i.e.
i.e. 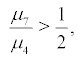 the boundary r = +∞ is exclusively natural.
the boundary r = +∞ is exclusively natural.
If 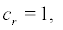 i.e.
i.e. 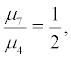 the boundary r = +∞ is exclusively natural.
the boundary r = +∞ is exclusively natural.
Thus we can draw the conclusion that the trivial solution r = 0 is unstable, i.e. the stochastic system is unstable at the equilibrium point Q no matter whether the deterministic system is stable at equilibrium point Q or not.
In the section, We will see how the introduction of randomness change the stochastic behavior significantly from both the dynamical and phenomenological points of view [21,22].
Theorem 4.1(D-bifurcation) Let 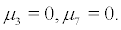 Then system (2) undergoes stochastic D-bifurcation.
Then system (2) undergoes stochastic D-bifurcation.
Proof. When 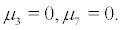 Then system (10) becomes
Then system (10) becomes
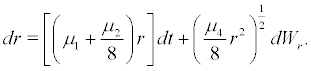 (18)
(18)
When 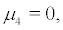 equation (18) is a determinate system, and there is no bifurcation phenomenon. Here we discuss the situation
equation (18) is a determinate system, and there is no bifurcation phenomenon. Here we discuss the situation 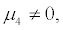 let
let
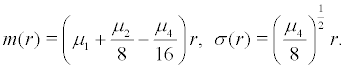
The continuous random dynamic system generate by (18) is
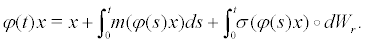
where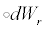 is the differential at the meaning of Statonovich, it is the unique strong solution of (18) with initial value x . And
is the differential at the meaning of Statonovich, it is the unique strong solution of (18) with initial value x . And 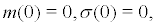 so 0 is a fixed point of ÃÂÃâ¢. Since m(r) is bounded and for any
so 0 is a fixed point of ÃÂÃâ¢. Since m(r) is bounded and for any 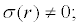 , it satisfy the ellipticity condition: σ (r) ≠ 0; it assure that there is at most one stationary probability density. According to the Itoˆ equation of amplitude r(t) , we obtain its FPK equation corresponding to (18) as follows
, it satisfy the ellipticity condition: σ (r) ≠ 0; it assure that there is at most one stationary probability density. According to the Itoˆ equation of amplitude r(t) , we obtain its FPK equation corresponding to (18) as follows
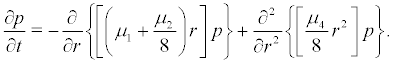 (19)
(19)
Let 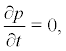 then we obtain the solution of system (19)
then we obtain the solution of system (19)
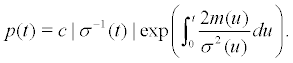 (20)
(20)
The above dynamical system (19) has two kinds of equilibrium state: fixed point and non-stationary motion. The invariant measure of the former is 0 δ and it’s probability density is . δx The invariant measure of the latter is ν and it’s probability density is (20). In the following, we calculate the lyapunov exponent of the two invariant measures.
Using the solution of linear Itô stochastic differential equation, we obtain the solution of system (18)
 (21)
(21)
The lyapunov exponent with regard to μ of dynamic system ÃÂÃ⢠is defined as:
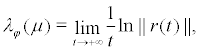 (22)
(22)
substituting (21) into (22) , note that 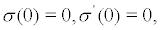 , we obtain the lyapunov exponent of the fixed point:
, we obtain the lyapunov exponent of the fixed point:
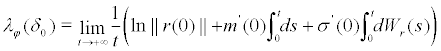
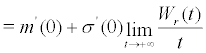
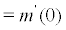
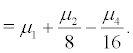 (23)
(23)
For the invariant measure which regard (21) as its density, we obtain the lyapunov exponent:
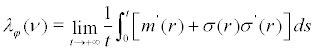
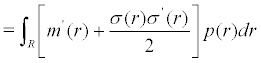
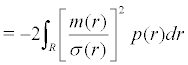
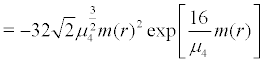
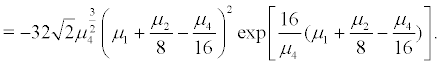 (24)
(24)
Let 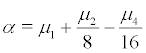 We can obtain that the invariant measure of the fixed point is stable when α < 0 , but the invariant measure of the non-stationary motion is stable when
We can obtain that the invariant measure of the fixed point is stable when α < 0 , but the invariant measure of the non-stationary motion is stable when 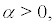 so
so 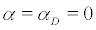 is a point of D -bifurcation. Then system (2) undergoes stochastic D-bifurcation.
is a point of D -bifurcation. Then system (2) undergoes stochastic D-bifurcation.
Theorem 4.2 Let 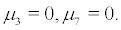 Then system (2) dose not undergo stochastic P-bifurcation.
Then system (2) dose not undergo stochastic P-bifurcation.
Proof. Simplify Eq. (20) , we can obtain
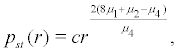 (25)
(25)
where c is a normalization constant, thus we have
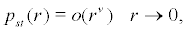 (26)
(26)
where 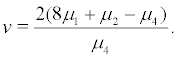 Obviously when
Obviously when 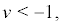 that is
that is 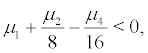
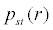 is a δ function. when
is a δ function. when 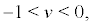 that is
that is 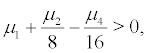 r = 0 is a maximum point of
r = 0 is a maximum point of 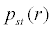 in the state space, thus the system occur D-bifurcation when v = −1, that is
in the state space, thus the system occur D-bifurcation when v = −1, that is 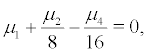 is the critical condition of D-bifurcation at the equilibrium point. When v > 0, there is no point that make
is the critical condition of D-bifurcation at the equilibrium point. When v > 0, there is no point that make 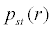 have maximum value, thus the system does not occur P-bifurcation.
have maximum value, thus the system does not occur P-bifurcation.
Theorem 4.3(P-bifurcation) Let 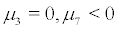 ,then system (2) undergo a P-bifurcation at the parameter value
,then system (2) undergo a P-bifurcation at the parameter value 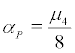
Proof. When 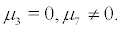 then Eq (10) can rewrite as following
then Eq (10) can rewrite as following
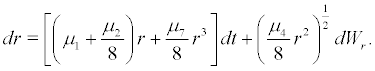 (27)
(27)
Let 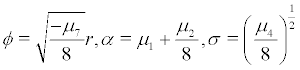 then we consider the system (27) becomes
then we consider the system (27) becomes
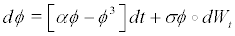 (28)
(28)
which is solved by
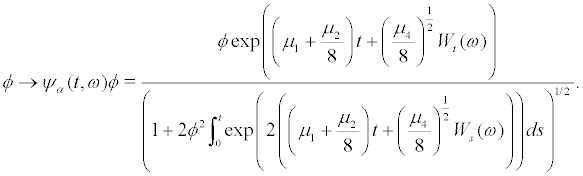 (29)
(29)
We now determine the domain 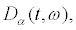 where
where 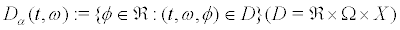 is the (in general possibly empty) set of initial values
is the (in general possibly empty) set of initial values 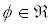 for which the trajectories still exist at time t and the range
for which the trajectories still exist at time t and the range 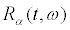 of
of 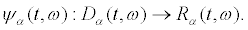
We have
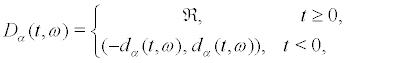 (30)
(30)
where
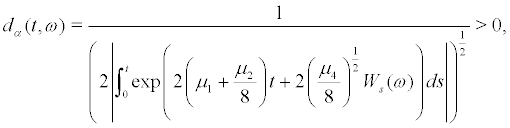
and
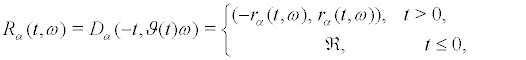 (31)
(31)
where
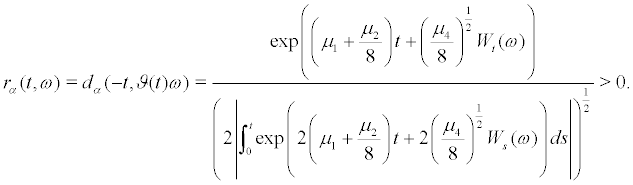
We can now determine
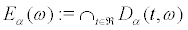
and obtain
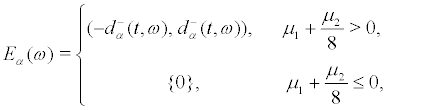 (32)
(32)
where
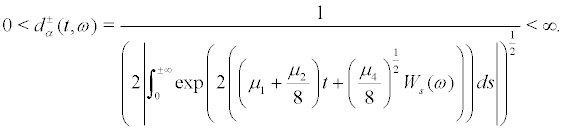
The ergodic invariant measures of system (27) are£º
(i) For 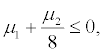 the only invariant measures is
the only invariant measures is 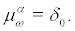
(ii) For 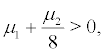 we have the three invariant forward Markov measures
we have the three invariant forward Markov measures 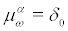 and
and 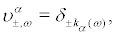 where
where 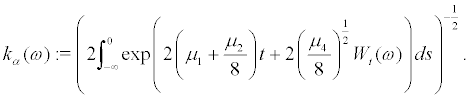
We have 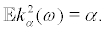 Solving the forward Fokkwer-planck equation
Solving the forward Fokkwer-planck equation
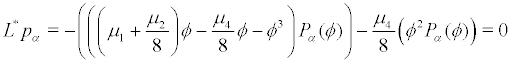
yield
(i) 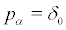 for all
for all 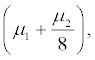
(ii) for 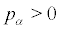
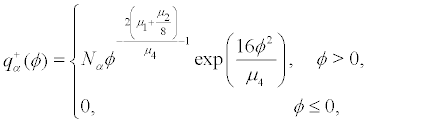
and 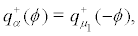 where
where 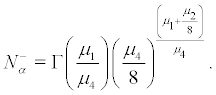
Naturally the invariant measures 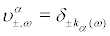 are those corresponding to the stationary measures q α+.Hence all invariant measures are Markov measures.
are those corresponding to the stationary measures q α+.Hence all invariant measures are Markov measures.
The two families of densities 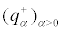 clearly undergo a P-bifurcation at the parameter value
clearly undergo a P-bifurcation at the parameter value 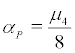 . Then system (2) undergo a P-bifurcation
. Then system (2) undergo a P-bifurcation
Theorem 4.4 Let 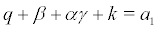 or
or 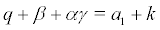 ,
, 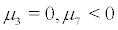 .Then system (2) undergoes stochastic pitchfork bifurcation.
.Then system (2) undergoes stochastic pitchfork bifurcation.
Proof.We determine all invariant measures(necessarily Dirac measure) of local RDS χ generated by the SDE
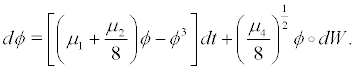 (33)
(33)
on the state space 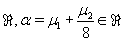 and
and 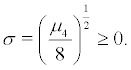 We now calculate the Lyapunov exponent for each of these measure.
We now calculate the Lyapunov exponent for each of these measure.
The linearized RDS 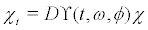 satisfies the linearized SDE
satisfies the linearized SDE
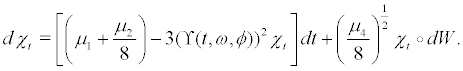
hence
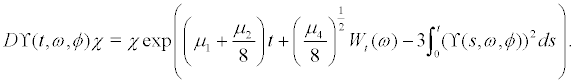
Thus, if 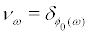 is a ϒ - invariant measure, its Lyapunov exponent is
is a ϒ - invariant measure, its Lyapunov exponent is
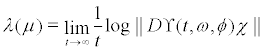
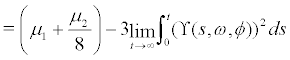
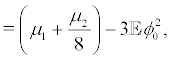
provided the IC 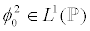 is satisfied.
is satisfied.
(i) For 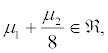 the IC for
the IC for 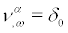 is trivially satisfied and we obtain
is trivially satisfied and we obtain
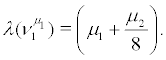
So ν1α is stable for 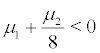 and unstable for
and unstable for 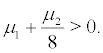
(ii) For 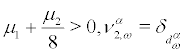 is
is  measurable, hence the density pα of
measurable, hence the density pα of 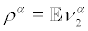 satisfies the Fokker-Planck equation
satisfies the Fokker-Planck equation
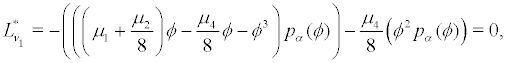
which has the unique probability density solution
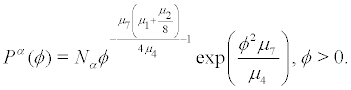
Since
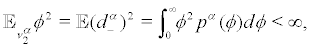
the IC is satisfied. The calculation of the Lyapunov exponent is accomplished by observing that
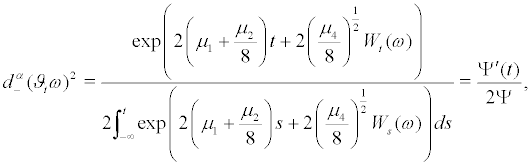
where
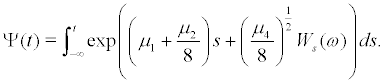
Hence by the ergodic thoerem
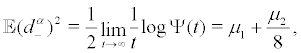
finally
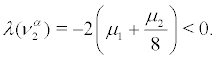
(iii) For 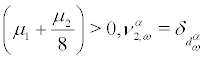 is
is 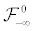 measurable. Since
measurable. Since 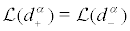
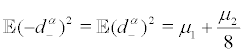
thus
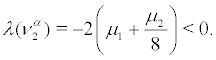
From Theorem 4.4, the two families of densities 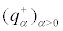 clearly undergo a P-bifurcation at the parameter value
clearly undergo a P-bifurcation at the parameter value 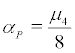 which is the same value as the transcritical case. Hence, we have a D-bifurcation of the trivial reference measure
which is the same value as the transcritical case. Hence, we have a D-bifurcation of the trivial reference measure 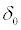 at
at 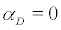 and a P-bifurcation of
and a P-bifurcation of 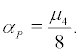 Then system (2) undergoes stochastic pitchfork bifurcation.
Then system (2) undergoes stochastic pitchfork bifurcation.
In this section, we give some examples to verify the thepretical results obtained in 3 and 4. Set 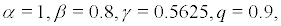 then Sys.(2) becomes
then Sys.(2) becomes
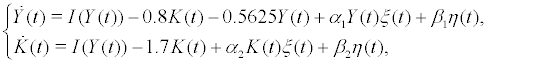 (34)
(34)
For simplicity, we assume that (0,0) is trivial equilibrium point of Sys.(34). Choose 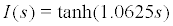 and then
and then 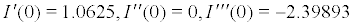 , (0,0) is asymptotically stability (Figures 1-7) .
, (0,0) is asymptotically stability (Figures 1-7) .
In this paper, we have considered a Kaldor-Kalecki model of business cycle with noise. Although there are lots of papers on the stability and Hopf bifurcation of Kaldor-Kalecki model of business cycle with delays, the method cannot be applied to the present model. By using the the singular boundary theory, Lyapunov exponent and the invariant measure theory, we have studied the a general third degree polynomial stochastic differential equation. Applying the obtained results to system (2), we have found that under certain conditions, when µ3 or µ7 varies, the zero solution loses its stability and Hopf bifurcation occurs, that is a family of periodic solutions bifurcate from the zero solution when µ3 or µ7 passes a critical. In addition, to provide a complete picture of the equilibrium behavior of the model as a parameter capturing the behavior changes of Kaldor-Kalecki model of business cycle, we conduct our analysis from the viewpoints of both dynamical and phenomenological bifurcations. Three numerical simulation results are given to support the theoretical predictions.
This research was supported by the National Natural Science Foundation of China (No. 11201089) and and (No.11301090). Guangxi Natural Science Foundation(No. 2013GXNSFAA019014) and (No. 2013GXNSFBA019016).