Data Hiding Using Difference Expension Method

Abstract

Ininverse order of datahidingtechniques,thevaluesoforiginal dataaremodifiedaccordingtosomeparticularrulesandtheoriginalhostcontentcanbeperfectlyrestoredafterextractionofthehidden dataonanotherside.Inthispaper,theoptimalruleofvaluemodificationunderapayloaddistortioncriterionisfoundbyusinganiterativeprocedure, andapracticalinverse order ofdatahidingschemeisproposed.Theembedded secret data,aswellastheauxiliaryinformationusedforcontentget back,arecarriedbythedifferencesbetweentheoriginalpixel valuesandthecorrespondingvaluesestimated fromthe neighbors.Here,the errors aremodifiedaccordingtotheoptimalvaluetransferrule.Also,theoriginalimageisdividedintoanumberofpixelsubsetsandtheauxil iaryinformationofasubsetisalwaysembeddedintotheestimationerrorsinthenextsubset.Areceivercansuccessfullypull outtheembeddedsecret dataand recovertheoriginalcontentinthe subsetswithanreverseorder.Thisway,agoodinverse order ofdatahidingperformanceis achieved.

Keywords

Distortion,payload,inverse order of datahiding.

INTRODUCTION

DATA hidingtechniqueaimstoembedsomesecretinformationintoacarriersignalbyalteringtheinsignificantcomponentsf orcopyrightprotectionorcovertcommunication.Ingeneralcases,thedataembeddingoperationwillresultindistortioninthehostsignal. However,suchdistortion,nomatterhowsmallitis and theyunacceptabletosomeapplications,e.g.,militaryandmedicalimages.Inthismethodtoimproveembedtheadditionalsecretmes sagewithareversiblemannersothattheoriginalcontentscanbeperfectlyrestoredafterextractionofthe hiddendata.

Anumberofreversibledatahidingtechniqueshavebeenproposed,andtheycanbesimplyclassifiedintothreetypes:lossless compressionbasedmethods,differenceexpansion methods andhistogrammodificationmethods.Thelosslesscompression basedmethodsmakeuse ofstatisticalredundancyofthehostmediabyperforminglosslesscompressioninordertocreateasparespacetoaccommodateadditi onalsecretdata.IntheRSmethod,forexample,anordinary-singularstatus isdefinedforeachgroupofpixelsaccordingtoaflippingoperationandadiscriminationfunction.Theentry ofRSstatusisthenlosslesslycompressedtoprovideaspacefordataembedding.Alternatively,theleastsignificantdigitsofpixelvalu esinan Larysystemortheleastsignificantbits( LSB)ofquantizedDCTcoefficientsinaJPEGimagecanalsobeusedtoprovidetherequireddat aspace.Intheinverse order ofdatahidingtechniques,aspareplacecanalwaysbemadeavailabletoaccommodatesecretdataaslongasthechosenitemiscompres sible,butthecapacitiesarelow.

Adata-hidercanalsoemployhistogrammodificationmechanismtorealizeinverse order ofdatahiding.Inthehostimageis divided into blockssized 4×4, 8×8, or 16×16, andgray valuesare mappedtoa onecircle.Afterpseudorandomlysegmentingeachblockintotwosub- regions,theHM r o t a t i o n ofthetwosub-regionsonthiscircle isusedtoembedonebitineachblock.Onthereceivingside,thehostblockcanberecoveredfromamarkedimageina reverseprocess.Payloadofthismethodislowsinceeachblockcanonlycarryon only onebit.Basedonthismethod,arobustlosslessdatahidingschemeisproposedinwhichcanbeusedforsemifragileimageauthentication. AtypicalHMmethodpresentedinutilizesthezeroandpeakpointsofthehistogramofanimageandslig htlymodifiesthepixelgray scalevaluestoembeddataintotheimage.Inabinarytreestructureisusedtoeliminatetherequirementtocommunicatepairsofpeaka ndzeropointstotherecipient,andaHMshiftingtechniqueisadoptedtopreventoverflowandunderflow.TheHMmechanismcanal sobeimplementedinthedifferencebetweensubsampledimagesandthepredictionerrorofhostpixelsandseveralgoodpredictionapproacheshavebe enintroducedtoimprovethe performanceofreversibledatahiding.Althoughtheoriginalhostcanbeperfectlyrecoveredafterdataextraction,adatahideralwayshopestolowerthedistortioncausedbydatahidingortomaximizetheembeddedpayload withagivendistortionlevel,inotherwords,toachieveagood“payload-distortion”performance.

OPTIMAL VALUE TRANSFER

This section will introduce a value transfer matrix for illustrating the modification of cover values in reversible data hiding. Then, an iterative procedure is proposed to calculate the optimal value transfer matrix, which will be used to realize reversible data hiding with good payload-distortion performance.

In reversible data hiding methods using DE or HM mechanisms, the particular data available for accommodating the secret data, such as pixel differences or prediction errors, are first generated from host image, and then their values are changed according to some given rules, such as difference expansion or histogram modification, to perform the reversible data hiding. Here, we use transfer matrix to model the reversible data hiding in available data. Denote the histogram of the available data as H = {…, h - 2, h – 1, h 0, h 1, h 2,…}, where h k is the amount of available data with a value k . We also denote the number of available data possessing an original value i and a new value j caused by data hiding as t i ,j , and a transfer matrix made up of t i , j as

In fact, the DE and HM reversible data hiding methods possess their corresponding transfer matrixes. For instance, in the typical difference expansion method, the difference between two adjacent pixels is doubled and the secret bit is embedded as the least significant bit of the new difference value, d’ = 2.d + b. (5) Here, d, d’, and b are the original pixel-difference, the new difference value, and the secret bit. That means a difference with original value d will be changed as 2d/(2d+1) when the secret bit is 0/1. Since the probabilities of 0 and 1 in secret data are same, h’ 2d = h’ 2d+1 = hd/2 , in other words, td,2d = td,2d+1 = hd/2. With the typical histogram modification method in after finding a peak point and a zero point of the original histogram, the gray values between them are shifted towards the zeros point by 1, and the pixels with values at the peak point will be kept or shifted by 1 towards the zeros point according to the secret bits to be embedded. Denote p and z as the gray values corresponding to the peak and zero points of histogram, and suppose p<z without loss of generality. Thus, h’ p= h’ p+1 = hd/2 and h’ x= hx-1 ( p+2 ≤ x ≤ z ), in other words, tp,p = tp,p+1 = hd/2 and tx-1, x = hx-1 (p+2 ≤ x ≤ z ). So, the transfer matrix is

By introducing the transfer matrix to model the modification of cover values, the difference expansion and histogram modification methods can be viewed as two special cases. For any transfer matrix, denote its rowss

Here, Δ is a given small positive value, and the purpose ofthe update operation is to decrease the largest λ( i , j , k) for equalizing all of λ( i , j , k) . 4. Calculate the distortion level D and the pure payload Pusing (8) and (16). The current T is just the optimal transfer matrix for the pure payload and the distortion level. Then, go to Step 2.Using the above-described procedure, the value of the computational complexity is higher. In practice, we should make a tradeoff between the precision and computational complexity.

REVERSIBLE DATA HIDING SCHEME

In the proposed scheme, the host hidden data, as well theauxiliary information used for content decryption, are carried by the differences between the host pixel-values and the corresponding values estimated from the neighbors, and the estimation errors are modified according to the optimal value transfer matrix. The optimal value transfer matrix is produced for maximizing the amount of secret data, i.e., the pure payload, by the iterative procedure described in the previous section. That implies the size of auxiliary information does not affect the optimality of the transfer matrix. By dividing the pixels in host image into two sets and a number of subsets, the data embedding is orderly performed in the subsets, and then the auxiliary information of a subset is always generated and embedded into the estimation errors in the next subset. This way, a receiver can successfully extract the embedded secret data and recover the original content in the subsets with an inverse order.

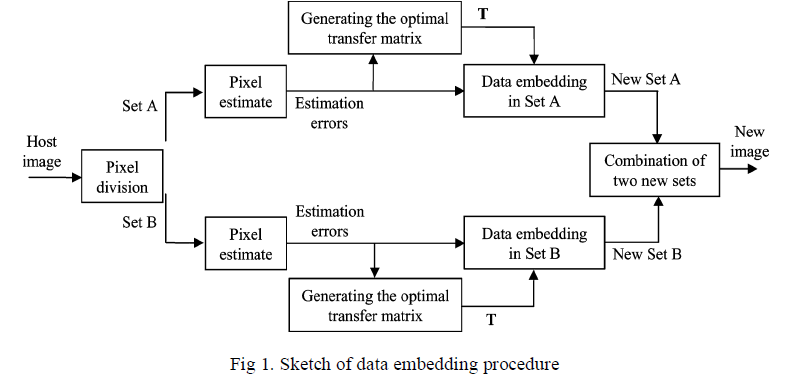A. Data Embedding

The data embedding procedure is sketched in Fig. 1. Denote the host pixels as pu,vwhere u and v are indices of row and column, and divide all pixels into two sets: Set A containing pixels with even (u+v) and Set B containing other pixels with odd (u+v). Fig. 2 shows the chessboard-like division. Clearly, the four neighbors of a pixel must belong to the different set. For each pixel, we may use four neighbors to estimate its value,

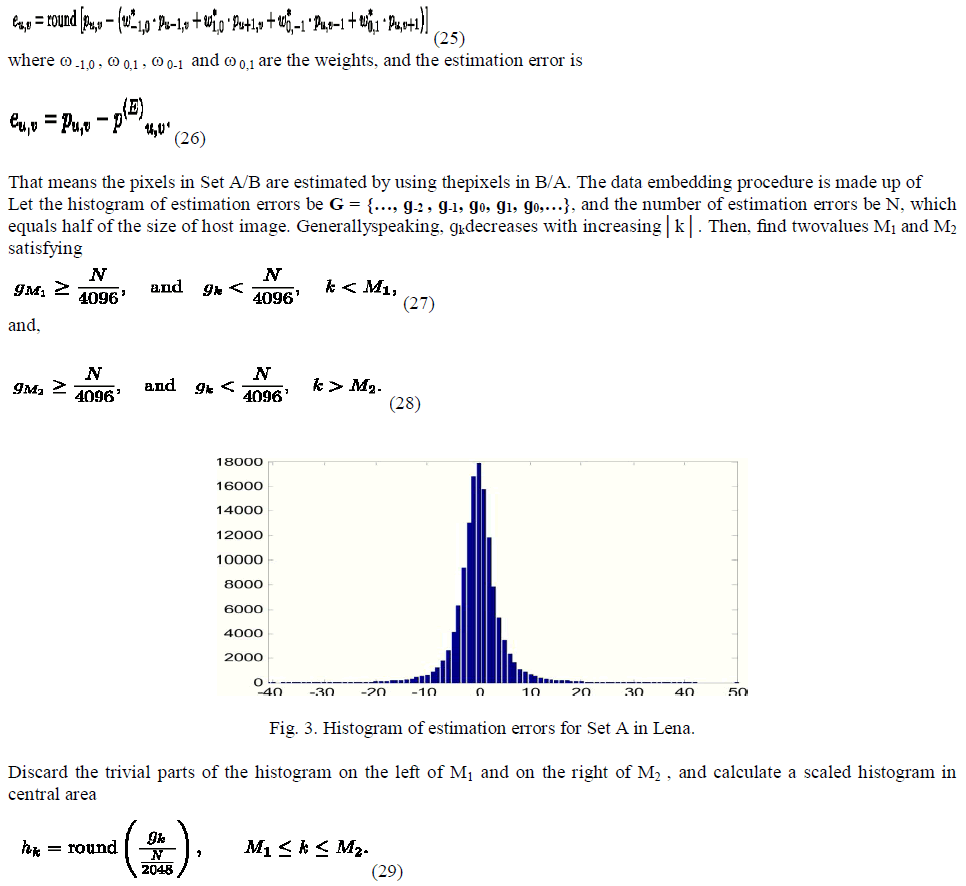Clearly, the scaled histogram on the left of M1 and on the right Of M2must be zeros, therefore will be ignored. For example, when a gray scale image Lena sized 512 × 512 was used as the host, the optimal estimation weights for Set A were ω * -1,0 = 0.406, ω* 0,1 = 0.408, ω* 0,-1 = 0.094 and ω* 0,1 = 0.093. The histogram of estimation errors G.

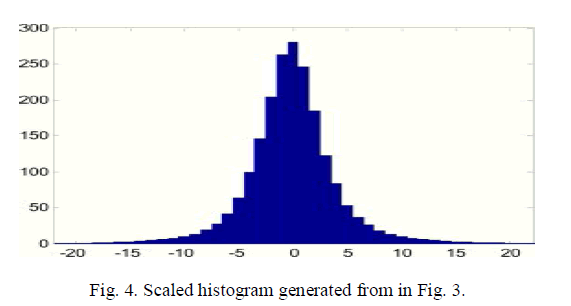around the diagonal. Fig. 5 gives an example of optimal transfer matrix generated from the histogram in Fig. 4by 4.0 × 104 iterations, in which the extreme white represents zero and the extreme black represents the maximal value in T. The computational complexity is proportional to the iteration number, and the generation of optimal transfer matrix can be finished in several seconds by a personal computer with 2.40 GHz CPU and 3.00 GB RAM.

B. Data Extraction and Content Recovery

Then, the receiver recovers the original content and extracts the hidden data in Subset NB - 1of Set B. Since the first part of AI NB – 1 contains the labels of saturated pixels and the original values of the first type of saturated pixels, the first type of saturated pixels in Subset NB – 1 can be localized and their original values can be recovered. For the second types of saturated pixels and the unsaturated pixels, after calculating the probability P0(ē) in (36), the receiver can convert the second part of AI NB – 1 into a sequence of original estimation error by arithmetic decoding. Thus, the original pixel values are recovered as

where P’ and e’ are the pixel value and estimation error in received image, and e is the original estimation error. Furthermore, with the original estimation errors e and the new estimation errors e’ , after calculating the probability PN(ē) in (34), the receiver can also retrieve the embedded data by arithmetic decoding

EXPERIMENTAL RESULTS

Four images, Lena, Baboon, Plane and Lake, all sized 512 × 512, shown in the host images. Both Set A and Set B were divided into 16 subsets. Since the auxiliary information of a subset is generated after data embedding and embedded into the next subset, we should ensure the capacity of a subset is more than the data amount of auxiliary information of the previous subset. This way, a receiver can successfully extract the embedded secret data and recover the original content in the subsets with an inverse order. On the other hand, the optimal transfer mechanism implemented in every subset except the last one is used to achieve a good payload-distortion performance. For the last subset, a LSB replacement method is employed to embed the auxiliary information of the second last subset and CB for content recovery with an inverse order. So, we hope the size of the last subset is small. Considering the two aspects, we make the subset sizes identical and let NA= NB = 16. In this case, the last subset occupies only 1/32 of cover data and almost does not affect the payload-distortion per

CONCLUSION

In order to achieve a good payload-distortion performance of reversible data hiding, this work first finds the optimal value transfer matrix by maximizing a target function of pure payload with an iterative procedure, and then proposes a practical reversible data hiding scheme. The differences between the original pixel-values and the corresponding values estimated from the neighbors are used to carry the payload that is made up of the actual secret data to be embedded and the auxiliary information for original content recovery. According to the optimal value transfer matrix, the auxiliary information is generated and the estimation errors are modified. Also, the host image is divided into a number of subsets and the auxiliary information of a subset is always embedded into the estimation errors in another subset. This way, one can successfully extract the embedded secret data and recover the original content in the subsets with an inverse order. The payload-distortion performance of the proposed scheme is excellent. For the smooth host images, the proposed scheme significantly outperforms the previous reversible data hiding methods. The optimal transfer mechanism proposed in this work is independent from the generation of available cover values. In other words, the optimal transfer mechanism gives a new rule of value modification and can be used on various cover values. If a smarter prediction method is exploited to make the estimation errors closer to zero, a best performance can be reached, but the computation complexity due to the prediction will be higher. The combination of the optimal transfer mechanism and other kinds of available cover data deserves further investigation in the future.

References

M. Goljan, J. Fridrich, and R. Du, “Distortion-free data embedding,” in Proc. 4th Int. Workshop on Information Hiding, Lecture Notes in Computer Science, 2001, vol. 2137, pp. 27–41. M. U. Celik, G. Sharma, A. M. Tekalp, and E. Saber, “Lossless generalized-LSB data embedding,” IEEE Trans. Image Process., vol. 14, no. 2, pp. 253–266, Feb. 2005. J. Fridrich, M. Goljan, and R. Du, “Lossless data embedding for all image formats,” in Proc. Security and Watermarking of Multimedia Contents IV, Proc. SPIE, 2002, vol. 4675, pp. 572–583.