ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| Prachi Patil Student of ME (Computer), AISSMS COE, Pune, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
A colossal data mining and knowledge discovery exhibits a great challenge with the volume of data growing at an unpredicted rate. Different techniques used to retrieve meaningful data. Rough set is one of them. This method is based on lower approximation, upper approximation. Existing method calculates rough set approximation in serial way. Therefore we propose a parallel method. Map-Reduce has developed to manage many large-scale computation. Recently introduced Map-Reduce technique has received much consideration from both scientific community and industry for its applicability in big data analysis. The effective computation of approximation is essential step in improving the performance of rough set. For mining the massive data, parallel computing modes, algorithms and different methods get used in research fields. In this paper, we have explained a parallel method for computing rough set. Using map-reduce we can achieve the same. Because of map-reduce we can generate rules and abstract attributes of massive data.
Keywords |
| Big Data; Map-Reduce; Rough Set; |
INTRODUCTION |
| From last few decennium, the size of the data stored in the databases has been increasing each day and therefore we face lots of difficulties about obtaining the worthful data. It has become difficult to reach accurate and useful information as the data stored in the databases is growing each day. To find out the rules or interesting and useful patterns within stored data in the databases, data mining techniques are used. Storing huge amount of increasing data in the databases, which is called information explosion, it is necessary to transform these data into necessary and useful information. Using conventional statistics techniques fail to satisfy the requirements for analyzing the data. |
| Data mining is a nontrivial process of determination of valid, unknown and potential useful and easily understandable dependencies in data. With the development of information technology, data volumes processed by many applications will routinely cross the peta-scale threshold, which will in turn increase the computational requirements. Data processing and knowledge discovery [1].For massive data is always a hot topic in data mining Data processing and knowledge discovery for massive data is always a hot topic in data mining. The big problem in data mining is the deficiency and indeterminateness. This problem is solved by using new theories and procedures, for example fuzzy sets, genetic algorithms or rough sets. |
II. RELATED WORK |
| In [1] author proposes a parallel method for computing rough set approximations. Consequently, algorithms corresponding to the parallel method based on the Map-Reduce technique are put forward to deal with the massive data. An extensive experimental evaluation on different large data sets shows that the proposed parallel method is effective for data mining. Enlarging data in applications make algorithms based on rough sets a challenging task. Since the computation of rough set approximations is the necessary step, the development of its efficient algorithms becomes an important task. Author has explained all the algorithm required for map-reduce. In paper [2], author explained the purpose of data mining for massive data, parallel computing modes and algorithms are typical methods in research fields. To mine knowledge from big data, he present consequently algorithm corresponding to the Map-Reduce based on roughest theory. In this paper comprehensive to evaluate the performances on the large data sets show that the proposed demonstrated can effectively process of big data. Author explained history of rough set and described with example [3]. He also introduced a knowledge discovery paradigm for multi-attribute and multi-criteria decision support, based on the concept of rough sets. Rough set theory provides mathematical tools for dealing with granularity of information and possible inconsistencies in the description of objects. In paper [4], the mathematical principles of rough sets theory are explained and a sample application about rule discovery from a decision table by using different algorithms in rough sets theory is presented. In the document author described basic concepts of rough set and its advantage. |
III. ROUGH SET |
| Rough set theory is a powerful mathematical tool created by Z. Pawlak in the beginning of the 1980s that has been applied widely to extract knowledge from database [1]. It discovers hidden patterns in data through the use of identification of partial and total dependencies in data. It also works with null or missing values. In decision making, it has confirmed that rough set methods have a powerful essence in dealing with uncertainties. Rough sets can be used separately but usually they are used together with other methods such as fuzzy sets, statistic methods, genetic algorithms etc. The RST has been applied in several fields including image processing, data mining, pattern recognition, medical informatics, knowledge discovery and expert systems. |
| Basically rough set is depend on approximation i.e. upper approximation and lower approximation as mentioned below which is calculated later in this paper. |
| ïÃâ÷ Lower approximation– The lower approximation consists of all the data without any ambiguity based on attributes. |
| ïÃâ÷ Upper approximation– The objects are probably belong to the set, cannot be described as not belonging to the set based on the knowledge of the attributes. |
| ïÃâ÷ Boundary region– The differences between these lower and upper approximations define the boundary region of the rough set. |
| The set is crisp, if boundary region is empty. Or set is rough, if the boundary region is nonempty. Rough set deals with vagueness and uncertainty emphasized in decision making. Data mining is a discipline that has an important contribution to data analysis, discovery of new meaningful knowledge, and autonomous decision making. The rough set theory offers a feasible approach for decision rule extraction from data. Rough set theory (RST) employed mathematical modeling to deal with class data classification problems, and then turned out to be a very useful tool for decision support systems, especially when hybrid data, vague concepts and uncertain data were involved in the decision process [6]. |
| Let T is decision table and T = (U, A) where U is universal set and A be the attribute set. If B A and X U We can approximate X using only the information contained in B by constructing the B-lower and B-upper approximations of X, denoted and respectively, where |
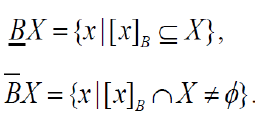 |
| There are many application associated with massive data, such as association rule mining, sequential pattern mining, text mining and temporal data mining, among the many algorithms based on rough set theory. Data stored in the databases is growing quickly, in addition to that effective use of the data is becoming a problem. Therefore data mining techniques are used to find out the rules or interesting and useful patterns from stored data. If data is incomplete or inaccurate, the results extracted from the database during the data discovery phase would be discrepant and nonmeaningful. Rough sets theory is a new mathematical approach used in the intelligent data analysis and data mining if data is uncertain or incomplete.[2] Rough set has great importance in cognitive science and artificial intelligence, decision analysis, expert systems and machine learning, inductive reasoning. |
IV. EXAMPLE |
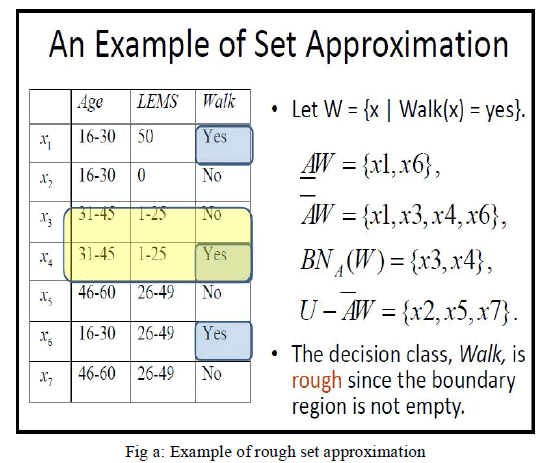 |
| As shown in above figure, there are two class attributes (Age, LEMS) and one decision attribute (Walk). We can generate rules from this table using rough set. The value of attribute Walk is only ‘yes’ or ‘no’. We are going to calculate approximation by considering decision attribute value ‘yes’. |
| As lower approximation contains data without ambiguity. In our example the object x1, x4, and x5 has value ‘yes’. We cannot add x4 in the set of lower approximation because the object x3 has the same class values as x4. It forms ambiguity. Therefore we exclude x4. In case of upper approximation, we choose objects having decision attribute value ‘no’. We found objects x2, x3, x5 and x7 having the decision value ‘no’. But this set contains the objects with ambiguity. In our example x3 has same class attribute value as x4 but different decision value. Such type of objects we can add in upper approximation. As a result, lower approximation of our decision table is {x1, x6} and upper approximation is {x1, x3, x4, x6}. As the boundary region is difference between these two sets, it contains objects {x3, x4}. Here boundary region is non-empty, hence it is rough set. |
V. MAP-REDUCE |
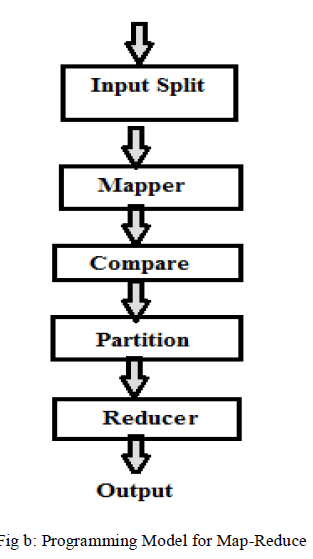
| Map-Reduce allows for distributed processing of the Map and Reduce functions.[2] The Map-Reduce divides the input file into no of blocks by method “input split”. It is used for processing data on commodity hardware. |
| Step 1: Input reader: |
| It divides the input into appropriate size splits i.e. blocks and assigns one split to each map function. The input reader reads data from stable storage and generates key/value pairs. |
| Step 2: Mapper |
| It process a key/value pair and generate another key/value pair. A number of such map functions running in parallel on the data that is partitioned across the cluster, produce a set of intermediate key/value pairs. |
| , |
| Step 3: Compare function |
| The input for each reduces is pulled from the machine where the map ran and stored using the applications comparison function. |
| Step 4: Partition Function |
| The partition function is given the key and the number of reducers and returns the indexes of the desired reduce. It is important to pick a partition function that gives an approximately uniform distribution of data reducers assigned more than their share of data for load-balancing operation to finish. |
| Step 5: Reducer |
| The reduce function then merge all intermediate values that are associated with the same intermediate key. |
| Step 6: Output |
| Map-Reduce allows developers to write and deploy code that runs directly on each data-node server in the cluster. That code understands the format of the data stored in each block in the file and can implement simple algorithms and much more complex ones. It can be used to process vast amounts of data in-parallel on large clusters in a reliable and fault tolerant fashion. Consequently, it renders the advantages of the Map/Reduce available to the users [2]. |
 |
| The rough set approximations obtained by the parallel method are the same as those obtained by the serial method. But using map reduce we can run independent phases in parallel as computing equivalence class, computing decision class, constructing associations based on map-reduce. Therefore time required is very less as compared to traditional method of rough set calculation. In addition to that we can also generate the rules for massive data and able to abstract attributes in more efficient way using map-reduce with rough set. |
VI. PROPOSED SYSTEM |
| Existing method for calculating rough set performs in-memory processing. Firstly, it calculates the equivalence class and then decision class. And at the last approximation of decision class calculated. Existing method calculates the rough set serially. It cannot deal with large data sets. Therefore we have proposed parallel method performs on the Hadoop platform which may remove the data size limit due to transparent spilling. |
| Data partitioning, fault tolerance, execution scheduling are provided by MapReduce framework itself. MapReduce was designed to handle large data volumes and huge clusters (thousands of servers). MapReduce is a programming framework that allows to execute user code in a large cluster. All the user has to write two functions: Map and Reduce.During the Map phase, the input data are distributed across the mapper machines, where each machine then processes a subset of the data in parallel and produces one or more <key; value> pairs for each data record. Next, during the Shuffle phase, those <key, value> pairs are repartitioned (and sorted within each partition) so that values corresponding to the same key are grouped together into values {v1; v2; :::}. Finally, during the Reduce phase, each reducer machine processes a subset of the <key, {v1; v2; :::}> pairs in parallel and writes the final results to the distributed file system. The map and reduce tasks are defined by the user while the shuffle is accomplished by the system.Even though the former pseudo code is written in terms of string inputs and outputs, conceptually the map and reduce functions supplied by the user have associated types. |
| Map (k1, v1) → list (k2, v2) |
| Reduce (k2, list (v2)) → list (v2) |
| Two programmer specified functions: |
| • Map |
| Input: key/value pairs (k1, v1) |
| Output: intermediate key/value pairs list (k2, v2) |
| • Reduce |
| Input: intermediate key/value pairs (k2, list (v2)) |
| Output: List of values list (v2) |
| That is, the input keys and values are drawn from a different domain than the output keys and values. The k1, k2 are the two different keys used in MapReduce phase and same as v1, v2 are the different values. The intermediate keys and values are from the same domain as the output keys and values. |
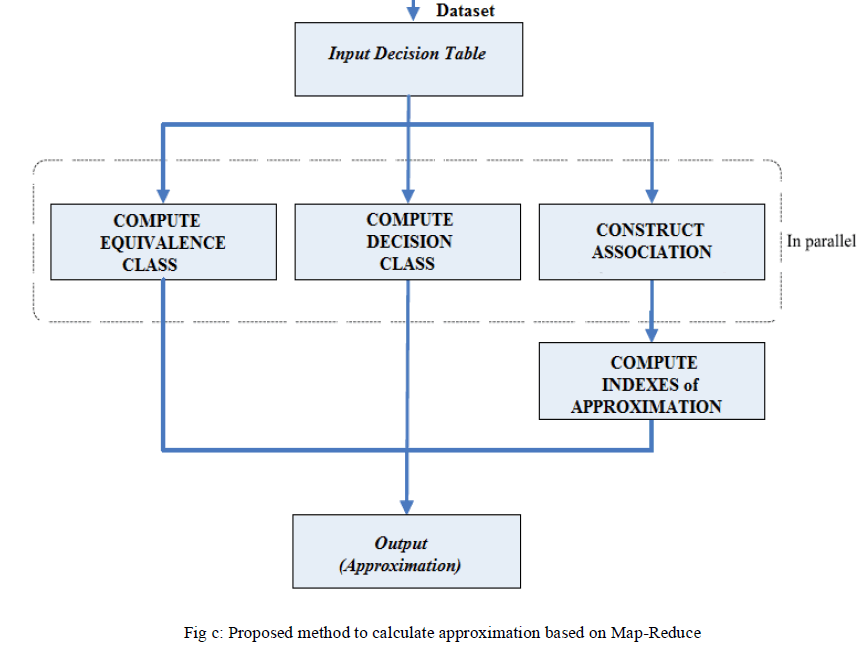
| In Proposed system we can compute both rough set equivalence classes and decision classes in parallel using theMap-Reduce technique. The associations between equivalence classes and decision classes of the decision table can also be executed in parallel. Lower and upper approximations are computed by associations between equivalence classes and decision classes. However, if we compute the approximations directly, memory may overflow since equivalence classes and decision classes both contain too many objects while dealing the large data set. Hence we can compute the Indexes of Rough Set Approximations i.e. the set of information for each decision class. After computing the indexes of approximations, we output the approximations directly. The diagram of the parallel method for computing rough set approximations is shown below. |
 |
| he rough set approximations obtained by the parallel method are the same as those obtained by the serial method. But using map reduce we can run independent phases in parallel as computing equivalence class, computing decision class, constructing associations based on map-reduce. Therefore time required is very less as compared to traditional method of rough set calculation. In addition to that we can also generate the rules for massive data and able to abstract attributes in more efficient way using map-reduce with rough set. |
| Map-Reduce framework offers clean abstraction between data analysis task and the underlying systems challenges involved in ensuring reliable large-scale computation. Map-Reduce runtime system can be transparently explore the parallelism and schedule components to distribute resource for execution. |
VII. CHARACERISTICS OF PROPOSED SYSTEM |
| We can measure the performance of proposed system using three characteristics as described below. |
| • Speed up: |
| To measure the speedup, we keep the data set constant and increase the number of nodes (computers) in the system. Speedup given by the larger system is defined by the following formula [8]: |
| Speedup (p) = T1 / Tp; |
| where p is the number of nodes (computers), T1 is the execution time on one node, Tp is the execution time on p nodes.We can perform the speedup evaluation on data sets with quite different sizes and structures. The number of nodes (computers) varied from one to many. In Serial existing system with p times the number of computers yields a speedup of p. However, linear speedup is difficult to achieve because the communication cost increases with the number of clusters becomes large. |
| • Scale up: |
| Scale up is defined as the ability of a p-times larger system to perform a p-times larger job in the same execution time [8]. |
| Scale up (D, p) = TD1/TDp |
| where D is the data set, TD1 is the execution time for D on one node, TDp is the execution time for p × D on p nodes.To check whether the proposed system handles larger data sets when more nodes are available. Therefore we can perform scale up experiments, where we can increase the size of the data sets in direct proportion to the number of nodes in the system. |
| • Size up: |
| Size up is defined as the following formula [8]: |
| Size up (D, p) = TSp/ TS1 |
| where TSp is the execution time for p × D, TS1 is the execution time for D.Size up analysis holds the number of computers in the system constant, and grows the size of the data sets by the factor p. Size up measures how much longer it takes on a given system, when the size of data set is p-times larger than that of the original data set. |
VII CONCLUSION |
| Up till now, many rough sets based algorithms have been developed for data mining. But enlarged data in applications made these algorithms based on rough sets a challenging task. Computation of rough set approximation is very important step. We can improve the quality and speed of calculating approximation. This is one way where we have lots of opportunities to achieve speed and accuracy. |
| In this paper, we proposed a parallel method for rough set. Using map-reduce we can achieve the same. Because of map-reduce we can generate rules and abstract attributes of massive data. Future work will involve the parallel frequent pattern mining exploration of an alternative method that calculate the attribute space, so that information systems with a large number of attributes, such as those used in mathematical, may be analyzed effectively. |
References |
|