International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Designing Of Fast Multipliers with Ancient Vedic Techniques

Jeevitha.R1, Jayanthi.P1, Gowthami A.K1, Uvarajan K.P2
  1. Assistant Professor, Dept. of ECE, Bannari Amman Institute of Technology, Sathyamangalam, India
  2. Assistant Professor, Dept. of ECE, KSR College of Engineering, Erode, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Vedic mathematics is an ancient system of mathematics which performs unique technique of calculations based on 16 sutras. The performance of high speed multiplier is designed based on Urdhva Tiryabhyam, Nikhilam Navatashcaramam Dashatah, and Anurupye algorithms. These algorithms gives minimum delay and used for multiplication of all types of numbers. The performance of high speed multiplier is designed and compared using these sutras for various NxN bit multiplications and implemented on the FFT of the DSP processor. Anurupye Vedic multiplier on FFT is made efficient than Urdhva tiryabhyam and Nikhilam Navatashcaramam Dashatah sutras by more reduction in computation time. Logic verification of these design is verified by simulating the logic circuits in XILINX ISE 9.1 and MODELSIM SE 5.7g using VHDL.

Keywords
Urdhva Tiryagbhyam, Nikhilam Navatashcaramam-Dashatah, Anurupye, Vedic multiplier.

INTRODUCTION
Multiplication is an important function in arithmetic operations. Multiply and Accumulate(MAC) is one of the frequently used Computation- Intensive Arithmetic Functions(CIAF) that are implemented in many Digital Signal Processing (DSP) applications such as convolution operation, filtering, Fast Fourier Transform(FFT) and in microprocessors in its arithmetic and logic unit(ALU) [2].
The demand for high speed processing has been increasing as a result of expanding computer and signal processing applications. High throughput arithmetic operation is important to achieve the desired performance in many image and real time processing applications. One of the arithmetic operations in such application is multiplication and the development of fast multiplier circuit. Reduction of both the time delay and power consumption is very essential requirements for many applications [3].
Multiplier design based on Vedic Mathematics is one of the fast and low power multiplier. Minimizing power consumption for digital systems is important and it involves optimization at all levels of the design. This optimization includes one technology that is used to implement the style, topology and the architecture of digital circuits.

VEDIC MATHEMATICS
Vedic mathematics is the part of four Vedas. Mainly it is a part of Sthapatya- Veda which is an upa-veda and a supplement of Atharva Veda. It gives various mathematical terms including arithmetic, geometry, trigonometry, factorization, calculus, etc. In the period of 1884-1960, Jagadguru Shankaracharya Bharati Krishna Teerthaji Maharaja comprised all this work together and gave its mathematical explanation while it is used for various applications. After extensive research in Atharva Veda, Swamiji constructed 16 sutras. But it is not found in present text of Atharva Veda because these formulae were constructed by Swamiji itself [6].
Vedic mathematics is not only a mathematical wonder but also it is used for logical operations. Vedic mathematics deals with various branches of mathematics like arithmetic, algebra, geometry etc. These methods and ideas are directly applied to geometry, trigonometry and applied mathematics. This is an interesting field and it gives some effective algorithms that can be applied to various branches of engineering such as computing and digital signal processing (DSP) [6].
A large amount of work has been done by understanding various methodologies of sutras. The16 sutras are as following:
• Chalana-Kalanabyham: Denotes “Differences and Similarities operation”.
• Ekanyunena Purvena: Denotes “By one less than the previous one operation”.
• Gunitasamuchyah: Denotes “The product of the sum is equal to the sum of the product operation”.
• Paraavartya Yojayet: Denotes “Transpose and adjusted operation”.
• Sankalana- vyavakalanabhyam: Denotes “By addition and subtraction operation”.
• Shunyam Saamyasamuccaye: Denotes “If the sum is same then it will be zero operation”.
• Urdhva-tiryagbhyam: Denotes “Vertical and crosswise operation”.
• Yaavadunam: Denotes “An extent of its deficiency operation”.
• (Anurupye) Shunyamanyat: Denotes “If one is in ratio, the other is zero operation”.
• Ekadhikina Purvena: Denotes “By one more than the previous one operation”.
• Gunakasamuchyah: Denotes “Factor of the sum is equal to sum of the factor operations”.
• Nikhilam Navatashcaramam Dashatah: Denotes “All from 9 and last from 10 operations”.
• Puranapuranabyham: Denotes “A complete or non complete operation”.
• Shesanyankena Charamena: Denotes “The remainders by the last digit operation”.
• Sopaantyadvayamantyam: Denotes “An ultimate and penultimate operation”.
• Vyashtisamanstih: Denotes “The Part and Whole operation”.

DESIGN OF HIGH SPEED VEDIC MULTIPLIER IN FFT
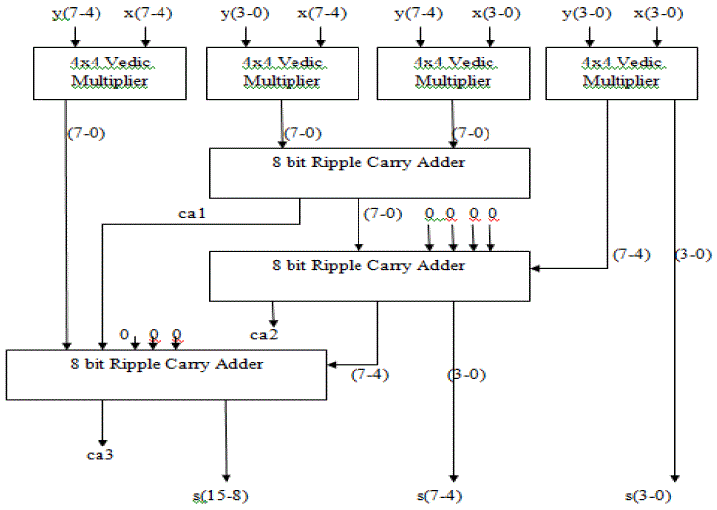
The Vedic multiplier which is designed based on “Urdhva Tiryagbhyam” sutra (algorithm) is a general multiplication formula applicable to all cases of multiplication and it means that “Vertically and Crosswise” and it is used for the multiplication of two decimal numbers. The advantage of this sutra is that it is based on novel concept through which the generation of all partial products can be done with the concurrent addition of partial products. This algorithm can be generalised for the design of n x n bit numbers. The multiplier is independent of clock frequency of the processor while calculating the partial products and their sums in parallel. Nikhilam Navatashcaramam Dashatah Vedic mathematical algorithm is done by “All from 9 and last from 10” and it is more efficient for large numbers. Anurupye sutra is done by “if one is in ratio, then the other is in zero operation”.
Digital signal processing (DSP) is the fastest growing technology that is important in almost all engineering discipline. Therefore, it possesses tremendous challenges to the engineering community. Fast operation of additions and multiplications are of extreme importance in DSP for digital filters, discrete Fast Fourier transforms etc..,

A.NIKHILAM NAVATASHCARAMAM DASHATAH SUTRA
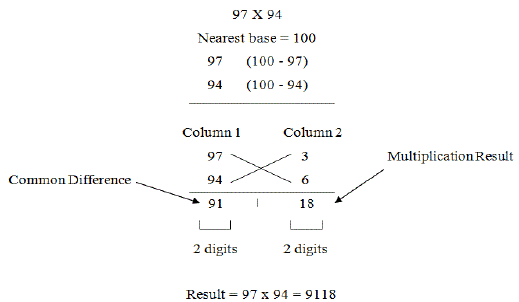
Nikhilam Sutra means “all from 9 and last from 10” multiplication operation. It is applicable for all cases of multiplication but it is more efficient for large numbers. Small numbers are also possible but complexity was increased. The multiplication operation is performed by found out the compliment of the large number from its nearest base. Hence the complexity is lesser for larger original number multiplication.
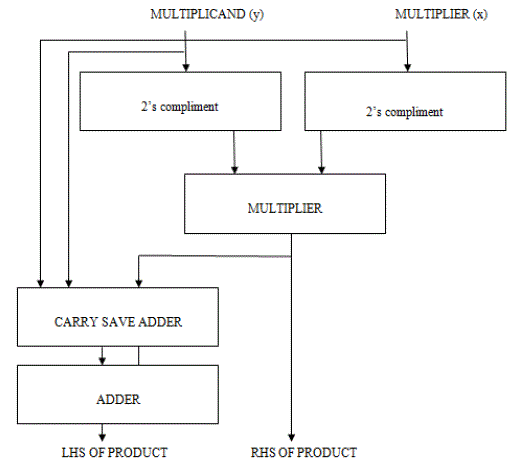
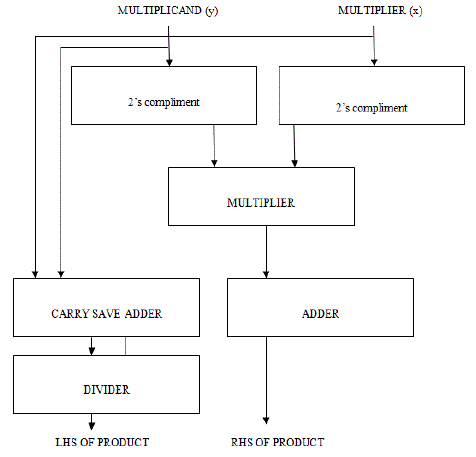
Nikhilam Sutra performs subtraction of a two number from its nearest power base i.e. 10, 100, 1000, etc. The difference is calculated from the power of 10 is called as Base. It is seen that the difference between the base and the number is Positive and hence it is called as NIKHILAM. The multiplication of two 8-bit numbers is reduced to the multiplication of their compliments and addition is shown in Fig.1
The Nikhilam sutra is applicable to both binary and decimal number system. The subtraction result of multiplicand and multiplier is represented by taking 2?s compliment of those two numbers. The right hand side (RHS) part of the product is implemented using 8x8 bit multiplier. The left hand side (LHS) part of the product is implemented using 8- bit carry save adder. If there is carry in RHS of product then it is added to LHS of product. The multiplication of 97 and 94 using Nikhilam sutra is shown in Fig.2.
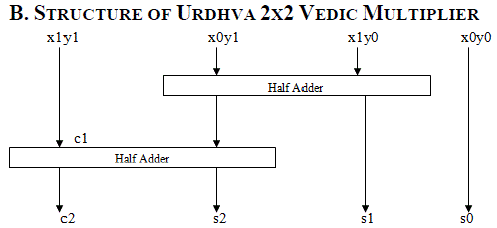
The method is described for both the 2 bit numbers X and Y where X = x1x0 and B = y1y0 as shown in Fig 3. In the first step the least significant bit of the final product (vertical) is obtained by multiplication of least significant bits of two numbers. In the second step the LSB of the multiplicand is multiplied with next higher bit of the multiplier. Then it is added with the multiplier product of LSB and next higher bit of the multiplicand (crosswise). Likewise this process is to be done concurrently.
The sum is obtained in second bit of the final product and the carry is added with partial product. By multiplying the most significant bits gives sum and carry. Digital multiplier architecture is developed by applying Urdhva tiryakbhyam Sutra to the binary number system. This is similar to the popular array multiplier architecture.
Another important multiplication algorithm is Booth multiplication. For high speed application large booth array is required and it provides the fast process of multiplying two numbers. Delay is the only time for the signals to propagate through the gates and the multiplication array is formed. An array multiplier is less economical because it requires a large no gates.

C. Multiplication of Two Decimal Numbers
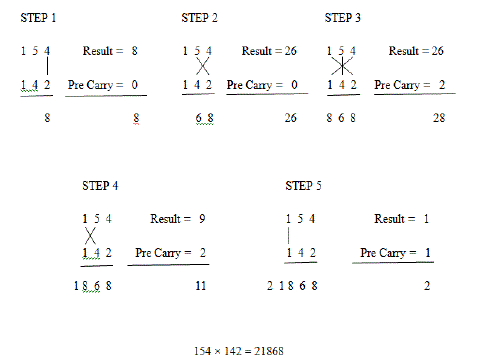
The Urdhva Sutra is illustrated by consider the multiplication of two decimal numbers 154 x 142 by Urdhva- Tiryakbhyam method as shown in Fig 5. The result is obtained by multiplying the digits on both sides of the line and added with the carry from the previous step. This generates result for one of the bits and carry. This process goes on by adding carry in the next step. If more than one line is present in one step then all the results are added to the previous carry. In every step, least significant bit (LSB) acts as a result bit and all other bits act as carry for the next step. Initially the value of carry is zero.

D. ANURUPYE (SHUNYAMANYAT) SUTRA
The upa-Sutra Anurupye means ‘proportionality’. This Sutra is used to find products of two numbers.The Common bases are 50, 60, 200 etc (multiples of powers of10).
The Anurupye sutra is illustrated by consider the multiplication of two decimal numbers 58 x 48 by Anurupye method as shown in Fig 7.

RESULTS AND DISCUSSIONS
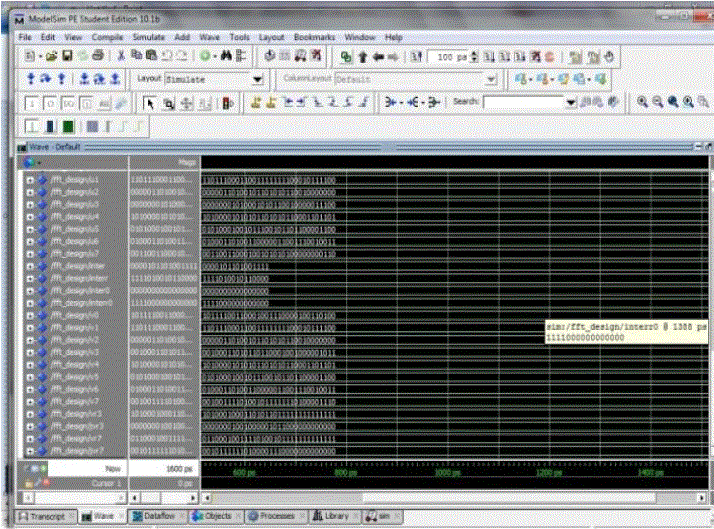
The Output window for 8x8 Anurupye Vedic Multiplier which was implemented in FFT is shown in Fig.8. It perform multiplication of two decimal numbers 58 x 48 by Anurupye method.
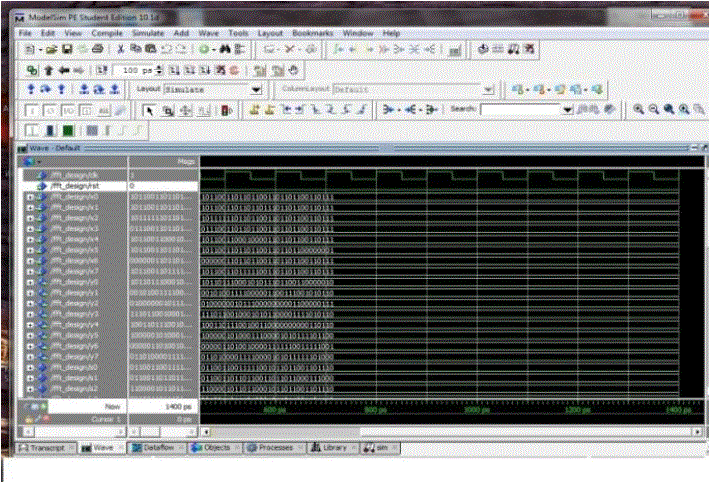
The Output window for 8x8 Urdhva Vedic Multiplier which was implemented in FFT is shown in Fig.9. It perform multiplication of two decimal numbers 154 x 142 by Urdhva-Tiryakbhyam method
The Output window for 8x8 Nikhilam Vedic Multiplier which was implemented in FFT is shown in Fig.10. It perform multiplication of two decimal numbers 97 x 94 by Nikhilam method.
The performance analysis of vedic multiplier with high speed and low delay are explained as in Table No.1.

CONCLUSION
Using Urdhva tiryabhyam and Nikhilam Navatashcaramam Dashatah sutras, multipliers were designed. Anurupye Vedic multiplier on FFT is made efficient than Urdhva tiryabhyam and Nikhilam Navatashcaramam Dashatah sutras by more reduction in computation time. Anurupye is used for multiplication of larger numbers.

Tables at a glance
Table icon
Table 1

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 1 Figure 2 Figure 3 Figure 4 Figure 5
Figure 6 Figure 7 Figure 8 Figure 9 Figure 10

References