Shortest Path problems are inevitable in road network applications such as city emergency handling and drive guiding system. Basic concepts of network analysis in connection with traffic issues are explored. The traffic condition among a city changes from time to time and there are usually huge amounts of requests occur, it needs to find the solution quickly. The above problems can be rectified through shortest paths by using the Dijkstra’s Algorithm. The main objective is the low cost of the implementation. The shortest path problem is to find a path between two vertices (nodes) on a given graph, such that the sum of the weights on its constituent edges is minimized. This problem has been intensively investigated over years, due to its extensive applications in graph theory, artificial intelligence, computer network and the design of transportation systems. The classic Dijkstra’s algorithm was designed to solve the singlesource shortest path problem for a static graph. It works starting from the source node and calculating the shortest path on the whole network. Noting that an upper bound of the distance between two nodes can be evaluated in advance on the given transportation network. In order to solve the problem, we have been implemented shortest path for road network by using Applets in a programing language java. Software required for this application is jdk1.7.0_01.
Keywords |
| shortest path; Dijkstra’s Algorithm; Breadth First Search; maximum number of nodes; |
INTRODUCTION |
| This paper involved in illustrating the best way to travel between two points and in doing so, the shortest path
algorithm was created. Dijkstra‘s Algorithm is a graph search algorithm that solves the single-source shortest path
problem for a graph with nonnegative edge path costs, producing a shortest path tree. This algorithm is often used in
routing and other network related protocols. For a given source vertex (node) in the graph, the algorithm finds the
Sfinding costs of shortest paths from a single vertex to a single destination vertex by stopping the algorithm once the
shortest path to the destination vertex has been determined. For example, if the vertices of the graph represent cities and
edge path costs represent driving distances between pairs of cities connected by a direct road, Dijkstra's algorithm can
be used to find the shortest route between one city and all other cities. |
| A large amount of work has been done on finding shortest paths through abstract. Dijkstra‘s algorithm is a
Shortest Path Finding Algorithm which is applicable on a Graph which is Directed and got the Edges weighted with
non-negative weights. If we have an undirected graph with edges unweighted, we can solve the problem with the
implementation of Breadth First Search (BFS) algorithm. As we know we are unableto use BFS algorithm in case of a
weighted and directed graph, but we can modify our algorithm of BFS in such a way that we can handle the above
stated issues (weights and direction). We will later know thatDijkstra‘s algorithm is asymptotically the fastest known
single-source shortest-path algorithm for arbitrary directed graphs with unbounded nonnegative weights. These are the
motivations‘that will help us to know further about the Dijkstra‘s algorithm. |
RELATED WORK |
| The indoor navigational assistance for this type of users [1] presents additional challenges not faced by conventional
guidance systems, due to the personal nature of the interactions. The algorithms are part of an overall Indoor
Navigation Model that is used to provide assistance and guidance in unfamiliar indoor environments. Path planning
uses the Dijkstra's shortestpathalgorithms, to operate on an "Intelligent Map", that is based on a new data structure
termed "cactus tree" which is predicated on the relationships between the different objects that represent an indoor
environment. This research explores the potential to design an application for the visually impaired even when to- date 'positioning and tracking' system cannot offer reliable position information that highly required by this type of
application.The best-path problem for public transportation systems[3], we found that the nature of transfer is that it
requires extra costs from an edge to its adjacent edge. So,we use the direct/indirect adjacent edges weighted directed
graph as a public transportation data model and improve the storage of an adjacency matrix. We introduce the space
storage structure in order to store the scattered information of transfer in indirect adjacent edges lists. Thus, we solve
the problem of complex network graphs' storage and design a new shortest path algorithm to solve transit problem
based on the data model.Algorithm analysis exhibits that the data model and the algorithm we propose are prior to a
simple graph based on the Dijkstra's algorithm in terms of time and space.Today, the increased traffic and complex
modern roadnetwork have made finding a good route[4] from one location to another a non-trivial task. Many search
algorithms have been proposed to solve the problem, and the most well-known being Dijkstra's algorithm, Johnson's
algorithm. While these algorithms are effective for path finding, they are wasteful in terms of computation. In this
paper, we present a study to examine both uninformed search and heuristic search based on some major cities and
towns.Efficient usage of routing algorithms [16] can significantly reduce travelling distance and transportation costs as
well. Usage of the shortest-path algorithm in this case Dijkstra's algorithm for inner transportation optimization in
warehouses. The model integrates data such as: 2D graph of warehouse layout, its 3D extension, historical data, ABC
analysis and business process model. The prototype of proposed application is tested with sample data and by
simulating different working conditions. |
DIJKSTRA’S ALGORITHM |
| Let the node at which we are starting be called the initial node. Dijkstra's algorithm will assign some initialdistance
values and will try to improve them step by step. For the first iteration, the current intersection will be the starting point
and the distance to it will be zero. For subsequent iterations (after the first), the current intersection will be the closest
unvisited intersection to the starting point—this will be easy to find. |
| From the current intersection, update the distance to every unvisited intersection that is directly connected to it. This is
done by determining the sum of the distance between an unvisited intersection and the value of the current intersection
and relabeling the unvisited intersection with this value if it is less than its current value. In effect, the intersection is
relabelled if the path to it through the current intersection is shorter than the previously known paths. To facilitate
shortest path identification, in pencil, mark the road with an arrow pointing to the relabelled intersection if you
label/relabel it, and erase all others pointing to it. After you have updated the distances to each neighbouring
intersection, mark the current intersection as visited and select theunvisited intersection with lowest distance (from the
starting point) – or the lowest label—as the current intersection. Nodes marked as visited are labelled with the shortest
path from the starting point to it and will not be revisited or returned to. |
 |
EXPERIMENTAL RESULTS |
| In this section, we conduct an experiment to compare the paths between the nodes. In that paths, the shortest path was
done by using dijkstra‘s algorithm. Here the shortest path it means low cost was found by the shortest path algorithm.
Here java code uses the applets so that applet viewer shows how the shortest path was done. With the use of java
software the result was shown in the report. We have got successful result. The experiment was successfully complete.
The result of this project finding the shortest path for a single source to to all pairs of vertices by using the Dijkstra’s
Algorithm. It gives the cheapest cost and its implementation is easy. |
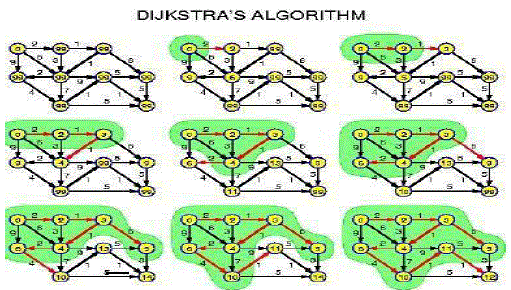
| A. Initial: |
| Algorithm running: Red arrows point to nodes reachable from the start node. |
| The distance to: b=55, d=50, f=100. Node d has the minimum distance. There is no other arrows coming in to d. Node
d will be colored orange to indicate 50 is the length of the shortest path to d. |
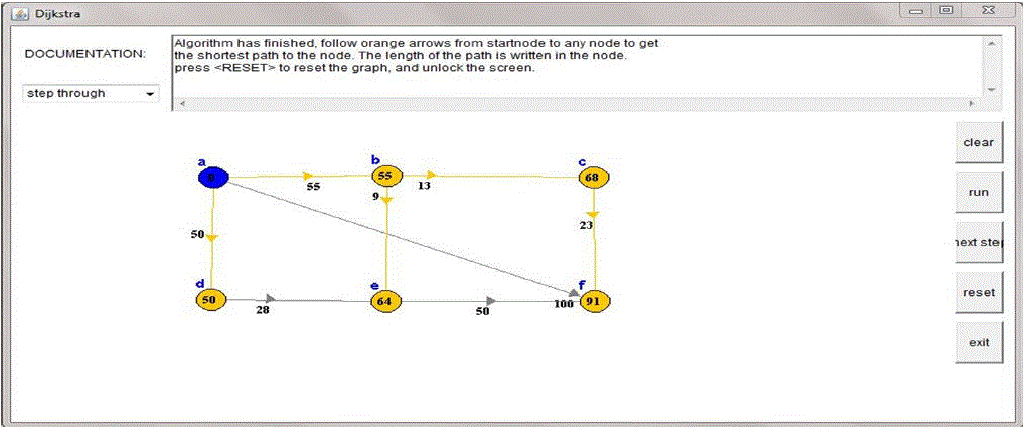
| B. Final : |
| Orange arrows point to nodes reachable from nodes that already have a final distance. The distance to: c=68.
There are no other arrows coming in to c. |
| Node c will be colored orange to indicate 68 is the length of the shortest path to c.Algorithm has finished,
follow orange arrows from start node to any node to get the shortest path to the node. |
CONCLUSION |
| We have proposed a practical algorithm for the shortest path problem in transportation networks. The proposed
algorithm can limit the search in a sub-graph based on the given nodes of the distance between the two nodes. As a
result, the calculation for the shortest path has been simplified. Experimental results on a real-world road network
reflect the potential characteristic of the proposed algorithm in comparison to the existing works. |
| Applets can prove to be very helpful to all the students, in general. Every student who wishes to learn one of the
algorithms, implemented in this tool, may use the proposed applet from any remote place, probably his home. It doesn’t
matter what his system is. It only requires that the Java Virtual Machine, (JVM), is installed into his system. It should
be pointed out that JVM is freely available for download from Sun Microsystems. Moreover there is an intention to
enhance the graph editor, in order that the user would be able to draw undirected graphs, or networks, as well. Yet this
applet could be further enriched, and possibly visualize more algorithms for digraphs. Directed networks such as the
Primal Simplex Algorithm which solves the Minimum Cost Network Flow Problem (MCNFP). Besides more
algorithms will be added for undirected graphs such as the Kruskal’s and Prim’s algorithms which solve the Minimum
Spanning Tree (MST) problem. |
FUTURE WORK |
| In future release the applet will be modified, in order to be executed as standalone Java application as well. In addition,
certain questionnaires will be given to the students of our department to be filled in, in order to get feedback. This is
very important, to improve and evaluate the teaching effectiveness of our applet in real instruction environment.
Students will also be encouraged to construct their own applets. |
| |
Figures at a glance |
 |
 |
| Figure 1 |
Figure 2 |
|
| |
References |
- Hua Wu; Marshall, A.; Yu, W., "Path Planning and Following Algorithms in an Indoor Navigation Model for Visually Impaired, " InternetMonitoring and Protection, 2007. ICIMP 2007. Second International Conference on , vol., no., pp.38,38, 1-5 July 2007.
- Reza SoltanAghaei, M.; Zukarnain, Z.A.; Mamat, A.; Zainuddin, H., "A Hybrid Algorithm for the Shortest-Path Problem in theGraph,"Advanced Computer Theory and Engineering, 2008. ICACTE '08. International Conference on , vol., no., pp.251,255, 20-22 Dec. 2008.
- Hongmei Wang; Ming Hu; Wei Xiao, "A new public transportation data model and shortest-path algorithms," Informatics in Control,Automation and Robotics (CAR), 2010 2nd International Asia Conference on , vol.1, no., pp.456,459, 6-7 March 2010.
- F. B. Zhan and C. E. Noon, Shortest Path Algorithms: An Evaluation Using Real Road Networks. Transportation Science. Vol.32, pp.65-73,February 1,1998.
- LixiaoGuo; Qiang Yang; Wenjun Yan, "Intelligent path planning for automated guided vehicles system based on topological map," Control,Systems & Industrial Informatics (ICCSII), 2012 IEEE Conference on , vol., no., pp.69,74, 23-26 Sept. 2012.
- Gene Eu Jan; Ming Che Lee; Hsieh, S.G.; Yung-Yuan Chen, "Transportation network navigation with turn penalties," Advanced Intelligent Mechatronics, 2009. AIM 2009. IEEE/ASME International Conference on , vol., no., pp.1224,1229, 14-17 July 2009.
- Abbas, M.A.; Chumachenko, S.V.; Hahanova, A.V.; Gorobets, A.A.; Priymak, A., "Models for quality analysis of computer structures," East-West Design & Test Symposium, 2013 , vol., no., pp.1,6, 27-30 Sept. 2013.
- Alzahrani, A.S.; Woodward, M.E., "End-to-end delay in localized QoS routing," Communication Systems,2008. ICCS 2008. 11th IEEESingapore International Conference on , vol., no., pp.1700,1706, 19-21 Nov. 2008.s
- Zhen Zhang; Wu Jigang; XinmingDuan, "Practical algorithm for shortest path on transportation network," Computer and InformationApplication (ICCIA), 2010 International Conference on , vol., no., pp.48,51, 3-5 Dec. 2010.
- Wu Jigang; Pingliang Han; Jagadeesh, G.R.; Srikanthan, T., "Notice of RetractionPractical algorithm for shortest path on large networks with time-dependent edge-length," Computer Engineering and Technology (ICCET),2010 2nd International Conference on , vol.2, no., pp.V2-57,V2-60, 16-18 April 2010.
- Wenyan Zhou; QizhiQiu; PengLuo; Pei Fang, "An improved shortest path algorithm based on orientation rectangle for restricted searchingarea," Computer Supported Cooperative Work in Design (CSCWD), 2013 IEEE 17th International Conference on ,vol., no.,pp.692,697, 27-29 June2013.
|