Keywords
|
| WSN, centralized, distributed, sensor network |
INTRODUCTION
|
| Wireless sensor networks are revolutionizing the ways to collect and use information from the physical world. This new technology has resulted in significant impacts on a wide array of applications in various fields, including military, science, industry, commerce, transportation, and health-care. However, the quality of sensors varies significantly in terms of their sensing precision, accuracy, tolerance to hardware/external noise, and so on. For example, studies show that the distribution of noise varies widely in different photovoltic sensors, precision and accuracy of readings usually vary significantly in humidity sensors, and the errors in GPS devices can be up to several meters. Thus, sensor readings are inherently uncertain. To facilitate management of uncertain data, research on probabilistic databases has received renewed attentions in the past few years. Most of the recent works on probabilistic data modeling propose to associate a confidence (in form of probability) with a data record/tuple to capture the data uncertainty and thus carry a possible world semantic. We first use an environmental monitoring application of wireless sensor network to introduce some basics of probabilistic databases. Consider a wireless sensor network that consists of a large number of sensor nodes deployed in a geographical region. Feature readings (e.g., moisture levels or speed of wind gust) are collected from these distributed sensor nodes. |
| Due to sensing imprecision and environmental interferences, the sensor readings are usually noisy. Thus, multiple sensors are deployed at certain zones in order to improve monitoring quality. In this network, sensor nodes are grouped into clusters, within each of which one of sensors is selected as the cluster head for performing localized data processing. By using statistic methods, a cluster head may generate a set of data tuples for each zone within its monitored region. In this example, we assume that each tuple is comprised of tuple id, zone, a derived possible attribute value, along with a confidence that serves as a measurement of data uncertainty. Thus, the data tuples corresponding to the same zone collectively represent the probabilistic distribution of derived possible values for the zone. Since the existence of possible values in these tuples is exclusive to each other, they naturally form a logical tuple, called x-tuple. Top-k queries on uncertain data have received increasing interests recently. Given a scoring function and a data set, a top-k query finds the highest ranked k tuples over all possible worlds. The answers to this query may vary in different possible worlds, making the problem interesting and challenging. Moreover, various semantics of top-k queries can be employed in different applications. |
DESIGN GOAL
|
| By using static methods, a cluster head may generate a set of data tuples for each zone within its monitored region. There are three proposed algorithm is to minimize the communication and energy overhead in responding to changing data distribution in the network. The algorithms are sufficient set-based (SSB) algorithm. The advantages of NSB and BB take advantage of the skewed necessary sets and necessary boundaries among local clusters to obtain their global boundaries, respectively, which are very effective for intercluster pruning. The transmission cost increases for all algorithms because the number of tuples needed for query processing is increased. |
Related work of top-K Query processing
|
| Moreover, various semantics of top-k queries can be employed in different applications. There are several top-k query semantics and solutions proposed recently, including U-Topk and UkRank, PT-Topk in, PK-Topk in, expected rank and so on. A common way to process probabilistic top-k queries is to first sort all tuples based on the scoring attribute, and then process tuples in the sorted order (until some termination condition is met) to compute the final answer set. Answer sets for the abovementioned queries typically consist of highly ranked tuples in the sorted list because tuples positioned lowly usually do not have the required ranks and confidence to be included in the answer sets. While these works produce insightful results, they are conducted on a centralized database rather than in a distributed setting as we target on in this paper. Only recently, a study on processing a probabilistic query with “expected rank” semantic in distributed systems has appeared. |
OVERVIEW
|
| Wireless sensor networks are revolutionizing the ways to collect and use information from the physical world. This new technology has resulted in significant impacts on a wide array of applications in various fields, including military, science, industry, commerce, transportation, and health-care. However, the quality of sensors varies significantly in terms of their sensing precision, accuracy, tolerance to hardware/external noise, and so on. For example, studies show that the distribution of noise varies widely in different photovoltic sensors, precision and accuracy of readings usually vary significantly in humidity sensors, and the errors in GPS devices can be up to several meters. Thus, sensor readings are inherently uncertain. To facilitate management of uncertain data, researches on probabilistic databases have received renewed attentions in the past few years. Most of the recent works on probabilistic data modeling propose to associate a confidence (in form of probability) with a data record/tuple to capture the data uncertainty and thus carry possible worlds semantic. |
| The distinction between digital and analogue has become tired and inappropriate. This is also true in the world of architectural drawing, which paradoxically is enjoying a renaissance supported by the graphic dexterity of the computer. This new fecundity has produced a contemporary glut of stunning architectural drawings and representations that could rival the most recent outpouring of architectural vision. |
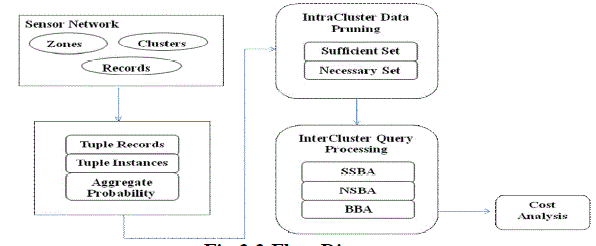
A Sensor Network
|
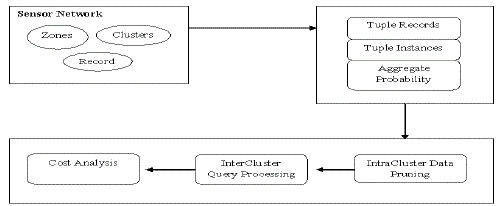
| A wireless sensor network that consists of a large number of sensor nodes deployed in a geographical region. Feature readings (e.g., moisture levels or speed of wind gust) are collected from these distributed sensor nodes. Due to sensing imprecision and environmental interferences, the sensor readings are usually noisy. Thus, multiple sensors are deployed at certain zones in order to improve monitoring quality. In this network, sensor nodes are grouped into clusters, within each of which one of sensors is selected as the cluster head for performing localized data processing. By using statistic methods a cluster head may generate a set of data tuples for each zone within its monitored region. Each tuple is comprised of tupleid, zone, a derived possible attribute value, along with a confidence that serves as a measurement of data uncertainty. Thus, the data tuples corresponding to the same zone collectively represent the probabilistic distribution of derived possible values for the zone. Since the existences of possible values in these tuples are exclusive to each other, they naturally form a logical tuple, called x-tuple. |
B Top-k Probability
|
| We define the tuple structure for each Zone. Then calculate the aggregate probability for all zones. Let W denote a possible world which consists of a subset of tuples in T and W denote the set of all possible worlds. The probability that w?W exists is |
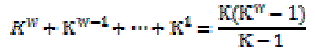 |
C Intracluster Pruning
|
| In a cluster-based wireless sensor network, the cluster heads are responsible for generating uncertain data tuples from the collected raw sensor readings within their clusters. We propose the notion of sufficient set and necessary set, and describe how to identify them from local data sets at cluster heads. Next, we use the PT-Topk query as a test case to derive sufficient set and necessary set and show that the top-k probability of a tuple t obtained locally is an upper bound of its true top-k probability. Given an uncertain data set Ti in cluster Ci. The sufficient boundary of Ti, SB(Ti) is the highest ranked tuple tsb such that the following condition is satisfied |
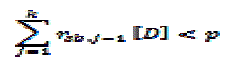 |
| Given an uncertain data set Ti in cluster Ci, the necessary boundary NB(Ti) is the lowest ranked tuple tnb such that: |
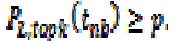 |
D Intercluster Query Processing
|
| The notion of sufficient and necessary sets as a basis, we propose three distributed algorithms for processing probabilistic top-k queries in wireless sensor networks, namely 1) Sufficient Set-based method; 2) Necessary Set-based method; and 3) Boundary-based method. Here we focus on addressing the communication overhead which is critical for wireless sensor networks and their applications. For simplicity, we logically assume single-hop transmission in both intracluster and intercluster communications. Nevertheless, our algorithms are not restricted to this assumption and can be extended for the multihop communications. As long as the base station receives all the candidate data tuples and supplementary tuples, we are able to compute the final answer with a generic centralized algorithm. Note that the supplementary tuples refer to the unqualified data tuples needed for computing the confidence probability of final answer. |
E Cost Analysis
|
| We first perform a cost analysis on data transmission of the three proposed methods. Let M denote the number of clusters in the network; and Sq,Sb, and Sd be the sizes of query message, boundary message, and data message, respectively. Also let |S(Ti)| and |N(Ti)| denote the cardinalities of the sufficient set and necessary set of the data set Ti in a cluster Ci(1<i<M), respectively. |
| The total transmission cost for SSB |
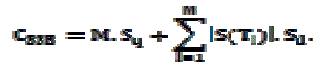 |
| The total transmission cost for NSB |
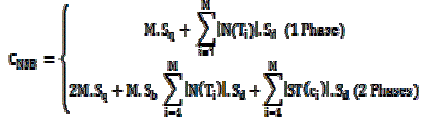 |
| The total transmission cost for BB |
Input and Output information
|
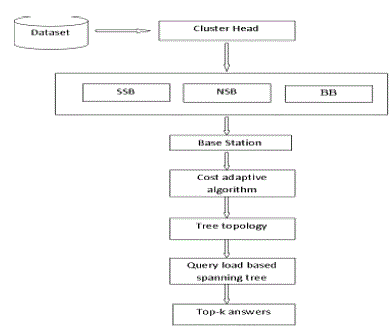
| ? Sensor Network – Network Details; Top-k Probability – Answer Set Probability; Intracluster Pruning – SS & NS Boundaries; Intercluster Query Processing – Final answer set |
| Cost Analysis – Cost for all sets |
OTHER ISSUES
|
| Confidentiality, integrity, availability, and authentication are four important security issues to be addressed in clusters connected by an unsecured public network. Rather than addressing all the security aspects, particular attention is confidentiality services for messages passed among computing nodes in an unsecured cluster. |
Sufficient Set-Based Algorithm
|
 |
EVALUATION
|
| In this section, we first conduct a simulation-based performance evaluation on the distributed algorithms for processing PTtop k queries in two-tier hierarchical cluster- based wireless sensor monitoring system. As discussed, limited energy budget is a critical issue for wireless sensor network and radio transmission is the most dominate source of energy consumption. Thus, we measure the total amount of data transmission as the performance metrics. Notice that, response time is another important metrics to evaluate query processing algorithms in wireless sensor networks. All of those three algorithms, i.e., SSB, NSB, and BB, perform at most two rounds of message exchange, thus clearly outperform an iterative approach (developed based on the processing strategy in [14]), which usually needs hundreds of iterations. Note that, there is not much difference among SSB, NSB, and BB in terms of query response time, thus we focus on the data transmission cost in the evaluation. Finally, we also conduct experiments to evaluate algorithms, SSB-T, NSB-T, and NSB-T-Opt under the tree-structured network topology. A value generated based on the node is location in order to inject spatial locality and is a random variable ranging from 0 to 1. When ¼ 1, the data distribution is highly spatial-correlated. When? ¼ 0, the data distribution is totally random. The real sensor traces are from the Intel Lab Data [35]. We treat the readings for each sensor node in the traces as for an area of interest by assigning readings to sensor nodes in an area. |
OVERALL PERFORMANCE
|
| We first validate the effectiveness of our proposed methods in reducing the transmission cost against two baseline approaches, including 1) a naive approach, which simply transmits the entire data set to the base station for query processing; 2) an iterative approach devised based on the |
CONCLUSION
|
| We propose the sufficient set and necessary set for efficient in-network pruning of distributed uncertain data in probabilistic top-k query processing. Introduce new algorithms namely SSB, NSB, and BB for in-network processing of PT-Top k queries. We derive a cost model on communication cost of the three proposed algorithms and propose a cost-based adaptive algorithm that adapts to the application dynamics. |
| |
Figures at a glance
|
 |
 |
 |
 |
| Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
| |
References
|
- A.D. Sarma, O. Benjelloun, A. Halevy, and J. Widom, “Working Models for Uncertain Data,”Proc. 22nd Int’l Conf. Data Eng. (ICDE ’06), p.7, 2006.
- C. Re, N. Dalvi, and D. Suciu, “Efficient Top-k Query Evaluation on Probabilistic Data,” Proc. Int’l Conf. Data Eng. (ICDE ’07), pp. 896-905,2007.
- M. Hua, J. Pei, W. Zhang, and X. Lin, “Ranking Queries on Uncertain Data: A Probabilistic Threshold Approach,”Proc. ACM SIGMOD Int’lConf. Management of Data (SIGMOD ’08),2008.
- F. Li, K. Yi, and J. Jestes, “Ranking Distributed Probabilistic Data,” Proc. 35th SIGMOD Int’l Conf. Management of Data (SIGMOD ’09),2009.
- Y. Diao, D. Ganesan, G. Mathur, and P.J. Shenoy, “Rethinking Data Management for Storage-Centric Sensor Networks,”Proc. Conf.Innovative Data Systems Research (CIDR ’07),pp. 22-31, 2007.
- M.A. Soliman, I.F. Ilyas, and K.C. Chang, “Top-k Query Processing in Uncertain Databases,”Proc. Int’l Conf. Data Eng. (ICDE ’07),2007
- C. Jin, K. Yi, L. Chen, J.X. Yu, and X. Lin, “Sliding-Window Top-k Queries on Uncertain Streams,”Proc. Int’l Conf. Very Large Data Bases(VLDB ’08),2008.
- G. Cormode, F. Li, and K. Yi, “Semantics of Ranking Queries for Probabilistic Data and Expected Ranks,”Proc. IEEE Int’l Conf. Data Eng.(ICDE ’09),2009.
- X. Liu, J. Xu, and W.-C. Lee, “A Cross Pruning Framework for Top-k Data Collection in Wireless Sensor Networks,”Proc. 11th Int’l Conf.Mobile Data Management,pp. 157-166, 2010.
- X. Lian and L. Chen, “Probabilistic Ranked Queries in Uncertain Databases,”Proc. 11th Int’l Conf. Extending Database Technology (EDBT’08), pp. 511-522, 2008.
|