Dynamic Architecture for Scalable and Proficient
Group Key Management

G M Mythili; N M Saravana Kumar

Dynamic Architecture for Scalable and Proficient Group Key Management

G M Mythili¹, N M Saravana Kumar²

PG Scholar, Department of CSE, Bannari Amman Institute of Technology, Sathyamangalam, Tamilnadu, India
Associate Professor, Department of CSE, Bannari Amman Institute of Technology, Sathyamangalam, Tamilnadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Network security plays important role in computer networks in both public and private, which are used in network transactions and communications such as businesses, government agencies and individuals. Key administration is one of the main errands in secure group communication systems. This paper proposes a cluster-based network and a secure and proficient key management scheme in multicast networks for achieving a secure communication between the group members. In this paper, process of generating self-invertible matrix for Hill Cipher algorithm has been proposed. The inverse of the matrix used for encrypting the message does not always available. If the matrix is not invertible, the encrypted message cannot be decrypted. In the self-invertible matrix generation process, the matrix used for the encryption is itself self-invertible. So, at the time of decryption, need not to find inverse of the matrix. This process decreases the computational complexity involved in finding inverse of the matrix while decryption. In this paper, we propose a secure and proficient key management scheme in multicast networks, Dynamic Architecture for Scalable and proficient Group Key Management, for achieving a secure communication between the communicating members in a cluster based network.

Keywords

multicast networks, key management, rekeying, secret sharing schemes, invertible matrix

INTRODUCTION

In internet world and the popularization of multicast networks, group-oriented communications, such as video conference, network games, and Video on demand, etc., play more and more vital roles. Secure group communication system provides confidentiality with matrix, user authentication, and information integrity, good scalability. Using the chosen key, the messages are protected by encryption. The context of group communication is called the group key. Only the group member knows the key for recover the original message. The group may require that membership changes produce the group to be rekeyed. Accessing the group communication from group members are prevented by changing the group key. When the key is changed with a member leave or join in group.

In the group communication all the designated receivers or members in a multicast group share a session encryption self-invertible matrix key. In many group communication applications, the multicast group membership modifies dynamically. Some new members are authorized to join a new multicast session, whereas some old members should be excluded. To ensure both forward secrecy and backward secrecy of multicast communications session keys shall change dynamically.

The matrix forward secrecy is maintained if a previous member who has been excluded from the current and future sessions cannot access the communication of the current and future sessions, and the backward secrecy is guaranteed if a new member of the current session cannot recover the communication data of past sessions. For authorized session members for each session, needs a new key that is only known to the present session members and session keys need to be dynamically distributed. Secure key distribution schemes for group communications allow establishing a secure multicast communication between a group manager and group members. The Perfect Group Communication contains Name abstraction, delivery, guarantees, reliability, ordering, group membership service, dynamic membership, multicast network, efficiency. Multicast communication uses network hardware support for broadcast or multicast when it is available over a distribution tree .

Goals of Group Communications are Information and ideas sharing and exchanging any project/policy/scheme are collected by information or feedback in groups To turn up at a decision on vital matters .Discuss about the issues related to a particular topic in relation to the group itself or for the benefit of a larger audience. Make elaborate upon any work undertaken or research done in order to elicit feedback management scheme .Key distribution plays an important role in network communication. All the key distribution protocol should be efficient and need to be more secure against the adversary attacks. The proposed key distribution scheme should be reliable to the large network size. This paper contains a scalable and reliable group key respect to the group communications with more security Organization as a whole member to solve a problem.

DYNAMIC ARCHITECTURE

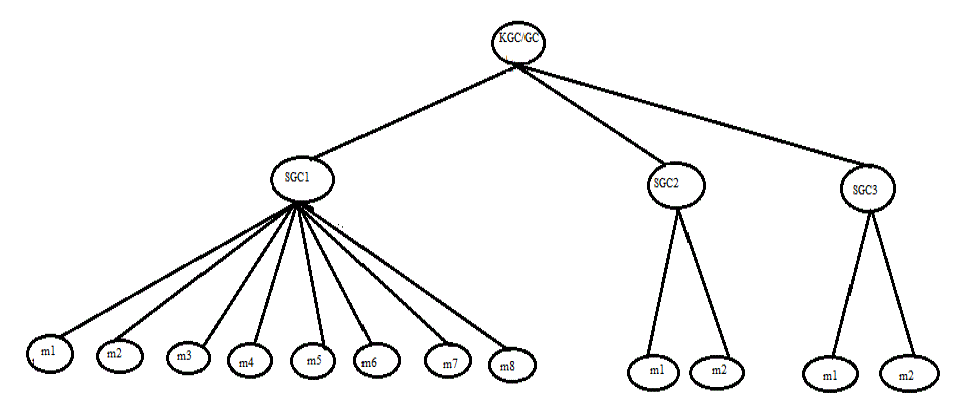
The multicast network in Dynamic Architecture has time-based cluster structure. Initially Key Generation Center/Group Controller (KGC/GC) assigns the number of sub-groups (cluster) to be constructed and their respective subscription span values based on which the members are grouped. For instance we consider the number of sub-groups under KGC/GC to be 3 whose subscription spans are 30 days, 6 months and 1 year respectively as shown in figure 1 where SGC1, SGC2, andSGC3 are sub-group controllers. Let there be 8 members with subscription span less than or equal to 30days who are to be grouped under SGC1, 2 members with subscription span more than 1 month endless than or equal to 6 months under SGC2, and 2 members with subscription span more than 6 months and less than or equal to 1 year under SGC3.

Sub-Group Key And Group Key Generation

The group key computation method used in [10] uses multi-party Diffe-Hellman and TGDH protocol to generate group keys. In Dynamic Architecture For Scalable and Efficient Group Key Management, we modify this idea by making the group key GK independent of sub-group key SGK.

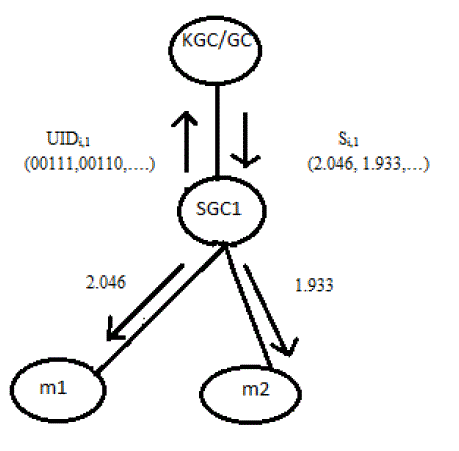
a) Generate sub-group Keys using Partial Keys from Members: Each member under a sub- partial key, ƒLi,j f Li,j to SGC, where i = 1, 2, 3, 4, .... and j = 1, 2, 3, .... The SGC then uses these partial keys to compute the subgroup keys (SGKs). Here, f is the generator of the multiplicative group, N Z* which is the set 1, 2,..., N − 1, N is the prime and L is a randomly chosen prime number for respective member. For example, from Figure 2, SGC1gets f L1,1L2,1L3,1L4,1 . Then each SGC adds its own partial key, fKj where j = 1, 2, 3, .., and computes the sub-group key. i.e. SGC1 adds its partial key say, f K1 . The resulting sub-group key of SGC1 is given bySGK1= f L1,1L2,1L3,1L4,1L5,1L6,1L7,1L8,1K1 …(1)The resulting SGK is sent to each member and is used for encryption and decryption of the message exchange among the members within the sub-group.

b) Generate Group Keys using the Partial Keys from SGCs.: The KGC/GC collects the partial key of each sub- group. Consider Figure 2. Let partial keys of SGCs are respectively. The KGC/GC receives f K1K2K3 and the group key, GK is computed by KGC/GC by adding its own partial keys as shown equation GK= f K1K2K3KGC …..(2)

Further, this Group key is broadcast to each sub-group which is used for decryption or encryption during the communication between different sub-groups under KGC/GC. The SGKs and GK are distributed in this network using proactive secret sharing scheme. For each GK and SGK to be distributed to the sub-groups and the members, a time periods , TGK and SGK , are set and divided into periods of time. Here, a proactive threshold scheme is applied, say (r + 1, t), where t is the number of time periods and r + 1 is the number of captions, say routers on the way between the sender and receivers, to be compromised by the adversary, who tries to learn the GK or SGK, in a single time period which is difficult as at the end of each time period, the share become obsolete and has to be erased. It is even difficult to distrust the secret by the adversary as t − r shares are to be corrupted in a single period of time.

Public-Private Keys and Signature Generation

Each user is given long-term public and private keys. The KGC/GC randomly chooses a secret key and the computes and publishes the corresponding public key. Dynamic Architecture For Scalable and Efficient Group Key Management uses the idea of RSA to construct a private-public key pair, where the KGC/GC calculates (1) public key (M, E), where M is the product of any two large prime numbers, a and b, and E is the number prime with respect to M and (2) private key (a, b, d, _(M )), where d is the part of private key of KGC/GC and is equal to mod _(M ). The KGC/GC determines a primitive element _ in GF(a) and GF(b). Then it chooses a one-way hash function. Here, (_, h()) is a public information where h() gives unique output for different input.

When a member creates a key-pair, then one key is kept as private and the other is the public-key which is uploaded to a server by the member where it can be accessed by any other member to send encrypted message. In secret sharing scheme, a secret is used as a beginning to generate a number of unique secrets, and those secrets are distributed and two or more secrets are combined to authenticate themselves and use the secret information. Secret sharing is also called secret splitting, key splitting, and split knowledge.

PUBLIC-PRIVATE KEYS AND SIGNATURE GENERATION

Each SGC provides UIDs of the member under it to the KGC/GC to obtain the signature Si,j of reach UIDi,j of a member mi,, where i = 1, 2, 3, ...., represents each member and j = 1, 2, or 3represents the SGC. If KGC/GC confirms the correctness and the relationship between mi,j and UIDi,j then it calculates Si,j using Equation 3 and distributes Si,j to each SGC where each SGC distributes them to the respective members. Si,j = UIDdi mod M ….(3)Both public-private keys pair and signatures are distributed using proactive secret sharing scheme.

REKEYING

Any member may leave or join the sub-group at any time. Whenever there is any change in the number of members in a sub-group, rekeying is done. In this section, the rekeying is discussed with respect to single leave, single join, multiple leaves and multiple joins situations in the group. In the database of KGC/GC, the data of the member is deleted and put in leaving member database as soon as the subscription span is finished,

Single leave,

1. Single member leave

2. Single member join

Multiple leaves,

1. Multiple leaves from the same sub group

2.Multiple leaves from the different sub group

Multiple Joins contains,

1. Multiple Joins in the same sub-group

2. Multiple Joins in the different sub-groups

MODIFIED HILL CIPHER

This algorithm generates the different key matrix for each block encryption instead of keeping the key matrix constant. This increases the secrecy of data in key distribution. Also algorithm checks the matrix used for encrypting the plaintext, whether that is invertible or not. If the encryption matrix is not invertible, then the algorithm modifies the matrix such a way that it’s inverse exist. The new matrix we obtain after modification of key matrix is called as Encryption matrix and with the help of this matrix encryption operation is performed. To generate different key matrix at every time, the encryption algorithm randomly generates the matrix which is also used as a key.

GENERATING SELF-INVERTIBLE MATRIX

This Hill cipher decryption needs inverse of the matrix, so while decryption a problem arises that is, inverse of the matrix does not always available. If the matrix is not invertible, then encrypted message cannot be decrypted. In order to overcome this problem, with help of self-invertible matrix generation method while encryption in the Hill Cipher. In the self-invertible matrix generation method, the matrix method used for the encryption is itself selfinvertible. So, at the time of decryption, need not to find inverse of the matrix. This method decreases the computational complexity involved in finding inverse of the matrix while decryption. A is self-invertible matrix if −1 A = A .

The analyses presented the generation of self-invertible matrix are valid for matrix of +ve integer numbers, they residues of modulo arithmetic on a prime number. The self-invertible matrix provides more security with group key and sub group key distribution in the group communication with respect of group members leave and join process. At the time of member leave or join sub group key calculated and distributed with matrix .The group key also calculated with matrix in the group communication.

OTHER BENEFITS

Dynamic Architecture For Scalable and Proficient Group Key Management achieves flexibility in the size of each sub-group i.e. any number of members can be joined in Dynamic Architecture For Scalable and proficient Group Key Management. Since the joining of a member is based on the subscription span and whenever subscription span is completed the member leaves the sub-group. The communications and key distributions in Dynamic Architecture For Scalable and Proficient Group Key Management ensure the security of the message exchanged between the members. . When an intruder tries to access the information being exchanged, it is difficult to obtain without the use of the required keys. In Dynamic Architecture For Scalable and proficient Group Key Management, only the communicating members know the subgroup keys, group keys, and other necessary keys required for the decryption of the data received. Even if the group key is static, the data cannot be accessed without the present sub-group key and other keys as the session keys change for each communication. If the intruder was the member under the group in past, it cannot access the data without its information being present in the database. Whenever a past member or a newly joined member tries to access any information, it is possible only if the session falls under their subscription span.

CONCLUSION

Dynamic Architecture For Scalable and Efficient Group Key Management is a systematic approach for the key management in a multicast network to achieve a great advantage in terms of scalability, forward secrecy, backward secrecy, key independence, etc. The number of sub-groups is constant and hence the group key remains same throughout. Hence, GK is generated and distributed only once. Dynamic Architecture for Scalable and Efficient Group Key Management uses proactive secret sharing scheme which is proven to be efficient for distribution of the keys. This algorithm is called Modified Hill Cipher Algorithm. This algorithm removes the drawback of using a random key matrix in this algorithm for encryption, need not be able to decrypt the encrypted message, if the matrix is not invertible. This paper provides efficient process for generating self-invertible matrix for Hill Cipher algorithm. These methods provide less computational complexity as inverse of the matrix is not required while decrypting in Hill Cipher.

Figures at a glance


Figure 1	Figure 2

References

XukaiZou, Byrav Ramamurthy and Spyros Magliveras 2002, ”Efficient Key Management for SecureGroupommunications with BurstyBehavior”. In Proceedings of the IASTED InternationalConference. Communications, Internet, and Information Technology.

Srinivasan T, Sathish S, Vijay Kumar R,.Vijayender M.V.B 2006, ”A Hybrid Scalable Group Key Management Approach for LargeDynamic Multicast Networks”.The Sixth IEEE InternationalConference on Computer and Information Technology.

MunivelE,Lokesh J 2008, “Design of Secure Group Key Management Scheme for MulticastNetworks using Number Theory”. CIMCA,IAWTIC, and ISE.

Anil Kapil, SanjeevRana 2009, ”Identity-Based Key Management in MANETs using Public Key Cryptography”. International Journal ofSecurity (I,JS), Vol(3), Issue(1).

A. J. Menezes, P.C. Van Oorschot, S.A. Van Stone, “Handbook of Applied Cryptography”,CRC press, 1996

Panja.B, Madria.S.K, Bhargava.B 2006., ”Energy and communication efficient group keymanagement protocol for hierarchical sensornetworks”. IEEE International Conference onSensor Networks, biquitous, and Trustworthy Computing, Vol(1).

Isabella Chang, Robert Engel, ”Key Management for Secure Internet Multicast using BooleanFunction Minimization Techniques”.Eighteenth Annual Joint Conference of the IEEEComputer and Communications Societies.Proceedings.IEEE INFOCOM’99. 1999.

Shu-Quan Li, Yue Wu 2010, ”A Survey on Key Management for Multicast”. Second InternationalConference on InformationTechnology and Computer Science.

Bibo Jiang, Xiulin Hu 2008, ”A Survey of Group Key Management”. International Conference on Computer Science and SoftwareEngineering.

PitipatanaSakarindr, NirwanAnsari 2007, “Elliptic Curve Cryptosystem based Group KeyManagement for Secure GroupCommunications”, Military Communications Conference,IEEE.

SenthamilIlango, Johnson Thomas 2004, ”Group Key Management utilizing Huffman and Petrickbased approaches”. Proceedings of theInternational Conference on Information Technology:Coding and Computing (ITCC’04).

Imai H., Hanaoka G., Shikata J., Otsuka A 2002., Nascimento A.C., “Cyptography with InformationTheoretic Security”, InformationTheory Workshop, 2002, Proceedings of the IEEE.