Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Efficient Data Broadcast Using One-To-All and All-To-All Broadcast Algorithm In Wireless Networks

S.BrittoRaj1 and A.Sivanesh Kumar2
  1. Assistant Professor
  2. Assistant Professor
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Broadcast communication is a key requirement for WSNs since many tasks in the network depend on broadcasting. Broadcasting has been one of the most significant and widely used communication techniques for information transformation. Broadcast communication, which forms the basis of all communication in wireless networks. In multihop wireless networks, however, interference at a node due to simultaneous transmissions from its neighbors makes it important to design a minimum-latency broadcast algorithm, which is known to be NP-complete. A simple 12-approximation algorithm for the one-to-all broadcast problem that improves latency Problem in the one-to-all broadcast algorithm. This leads to better performance with a collision free broadcasting. The all-to-all broadcast crisis where each node sends its own message to all other nodes. For all-to-all broadcasting the performance is improved by using Collect and Distribute, Interleaved Collect and Distribute algorithm. The message transmission in the wireless network using one-to-all and all-toall broadcast algorithm best result. But it is not enough for very large multihop networks, so in future it can be implemented for very large multihop networks in efficient manner to reduce latency and collision-free and to find the latency time in wireless networks. We can increase the performance in multihop networks over the existing system.

INDEX TERMS
Wireless networking, approximation algorithms, broadcast algorithms, wireless scheduling.

INTRODUCTION
NETWORK-WIDE broadcasting is a fundamental operation in wireless networks, in which a message needs to be transmitted from its source to all the other nodes in the network. There may be multiple messages to be broadcasted from multiple sources. Given that key applications of multihop wireless networks include prompt object detection using sensors, the design of low-latency broadcasting scheme is essential to meet stringent end-to-end delay requirements for higher-level applications. Interference is a fundamental limiting factor in wireless networks. When two or more nodes transmit a message to a common neighbor at the same time, the common node will not receive any of these messages. In such a case, we say that collision has occurred at the common node. Interference range may be even larger than the transmission range, in which case a node may not receive a message from its transmitter if it is within the interference range of another node sending a message. Approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems, since it is unlikely that there can ever be efficient polynomial-time exact algorithms solving NP-hard problems. One of the earliest broadcast mechanisms proposed in the literature is flooding [1], [2], where every node in the network transmits a message to its neighbors after receiving it. Although flooding is extremely simple and easy to implement, Ni et al. [3] show that flooding can be very costly and can lead to serious redundancy, bandwidth contention, and collision: a situation known as broadcast storm.
A. Our Contributions
We present algorithms for ONE-TO-ALL and ALL-TO-ALL broadcasting problems. In one-to-all broadcast, there is a source that sends a message to all other nodes in the network. In all-to-all broadcast each node sends its own message to all other nodes. Even the one-to-all broadcasting problem is known to be NP-complete [4]. For both problems, we develop approximation algorithms, which improve the previous results. For ONE-TO-ALL BROADCAST problem, we present a simple approximation algorithm that achieves a 12-approximate solution, thereby improving the approximation guarantee of 16. Our algorithm is based on the algorithm of Gandhi et al. [4] and incorporates the following two ideas that lead to the improvement: 1) processing the nodes greedily—in non increasing order of the number of receivers, and 2) allowing nodes to transmit more than once. For the ALL-TO-ALL BROADCAST problem we present two algorithms (called CDA and ICDA) with approximation guarantees of 20 and 34, respectively, thereby improving the approximation guarantee of 27. In ICDA, all nodes are scheduled to participate in transmissions as early as possible. Our algorithms achieve up to 37 percent improvement on end-to-end latency over existing schemes.

RELATED WORKS
Several techniques have been proposed for broadcasting in wireless networks. In order to reduce the broadcast redundancy and contentions, they make use of nodes’ neighborhood information and determine whether a particular node needs to transmit a message [5], [6]. There has been some work on latency-constrained broadcasting in wired networks [7] and some results do exist for radio networks whose models are essentially the same as ours. This result does not directly extend to ad hoc networks which are modeled by a restricted class of geometric graphs called disk graphs. Gandhi et al. [4] show that minimizing broadcast latency in wireless networks is NP-complete and then present an approximation algorithm for one-to-all broadcasting.
A. Network Model
When the interference range and the transmission range are identical, a wireless network can be modeled as a unit disk graph (UDG), G(V,E). The nodes in V are embedded in the plane. Each node u has a unit transmission range. Let uj; vj denote the Euclidean distance between u and v. We assume that time is discrete. We assume that every message transmission occupies a unit time slot: i.e., the latency of a single successful transmission is one unit of time. We say that there is a collision at node w, if w hears a message from two transmitters at the same time. In such a case, we also say that the two transmissions interfere at w. A node w receives a message collision free iff w hears the message without any collision.
B. Problem Statement:
Disk graph G= (V, E) and a set of messages M=(m1; m2; . . .;mn).A set of sources for these messages are taken as sources: (sj|sj is the source of message j). A node can transmit message j only after it receives message j collision free. A schedule specifies, for each message j and each node i, the time at which node i receives message j collision free and the time at which it transmits message j. If a node does not transmit a message then its transmit time for that message is 0. The latency of the broadcast schedule is the first time at which every node receives all messages. The number of transmissions is the total number of times every node transmits any message. The goal is to compute a schedule in which the latency is minimized. For that one-to-all and many-to-all broadcasting is used. One-to-all broadcasting is the operation where there is one source node s which has a message to send all other nodes. In all-to-all broadcasting each node v has its own message m to send all other nodes.

ONE-TO-ALL BROADCAST ALGORITHM
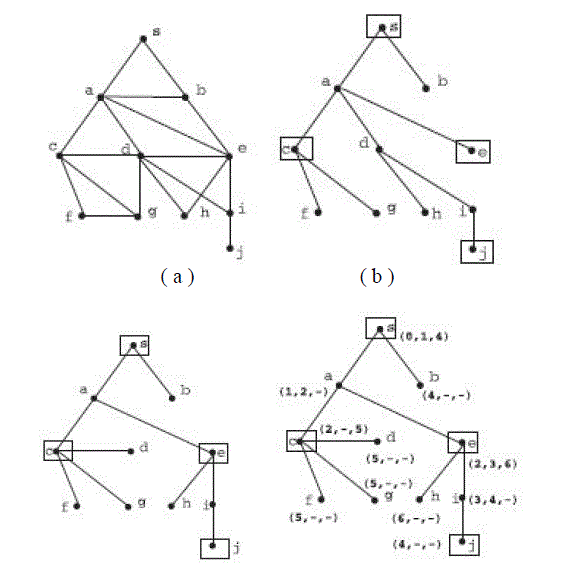
This algorithm takes the input and a source node s. If a node u is parent node of the node w then u is responsible for transmitting the message to w without any collision. This algorithm leads to significantly improved approximation guarantee are 1. Processing node in a greedy manner 2. Allowing a node to transmit more than once. It leads to guarantee that receiver node will receive the message collision free by overcoming broadcast problem. This algorithm first constructs BFS Tree. In BFS the non increasing order of nodes are the primary nodes. The children of the primary nodes are secondary nodes. In ONE-TO-ALL BROADCAST, the transmissions are scheduled in two phases. In Phase 1, the algorithm schedules transmissions only to the nodes in set X which contains all primary nodes and non leaf secondary nodes in the tree. In Phase 2, transmissions are scheduled to send the message to all other nodes. In Phase 1, nodes are considered one level at a time starting from Level 0. Only those primary nodes that have a child will transmit the message in this phase. The Primary nodes that doesn’t have child will transmit in the phase 2.

ALL-TO-ALL BROADCAST ALGORITHM
In all to all broadcast, every node in the network will transmits the message to every other node in the network. To overcome problem we change the value in approximation ratio as 20 and 34 using Collect and Distributed Algorithm(CDA) and Interleaved Collect and Distribute Algorithm(ICDA). In terms of transmission overhead, our algorithm shows that both CDA and ICDA consistently use fewer transmissions than existing one.
A. Collect-and-Distribute Algorithm (CDA)
The algorithm consists of 2 phases. In phase 1, source node collects all the packets by performing upward transmissions. In the Phase 2, source node broadcasts all the n packets to all other nodes via downward transmissions.
Phase 1. The source node collects all messages. The algorithm is as follows: first construct a BFS tree from s, and sort messages in non decreasing order of the level in the BFS tree. That is, messages that are closer to s appear first in the sorted list. Let us assume that message j be the jth message in the sorted order. The latency of the collection algorithm is at most reduced.
Phase 2. We construct a broadcast tree. Next, we describe transmission scheduling algorithm. In the algorithm by Gandhi et al. [4], the root node collects all messages and performs one-to-all broadcasting for each message. The root node needs to wait until the previous message reaches the level before initiating a broadcast for another message to make sure there are no collisions in their algorithm. In this algorithm, we find a schedule by a vertex coloring, which makes sure that all the nodes with the same color can broadcast a message without collision, and show that 17 colors are enough to obtain a collision-free schedule. Then computing the broadcast tree and let k1,k2 be the number of colors. We define a superstep for k time slots. In each superstep, the first k1 slots are for scheduling transmissions from primaries, and the remaining k2 slots will be for secondaries. Each primary with color i is only allowed to transmit in the ith slot of a primary slot in a superstep. Each secondary receiving a packet in a superstep transmits the received packet in the corresponding secondary slot in the same superstep.
B. Interleaved Collect-and-Distribute Algorithm (ICDA)
In the early stages of the algorithm, until s receives all the messages and starts propagating them, most nodes are idle, thus increasing the broadcast time significantly. Thus it describes an algorithm in which all nodes participate in broadcasting as soon as possible so as to minimize the broadcast time. A node v receives a message m forwarded originally from its descendant x in the broadcast tree and relays it to its parent to deliver the message to the root node s.The children of v can also receive the message when v broadcasts it. Using the broadcast tree constructed as in CDA, we schedule transmissions for each node as follows: as in CDA, we define a superstep but in a slightly different way. That is, in each superstep, every node transmits at most one message (either upward or downward). Instead of finishing all upward transmissions first, we mix upward or downward transmissions in each superstep with preferences given to upward transmissions.
C. Results for One-to-All Broadcast
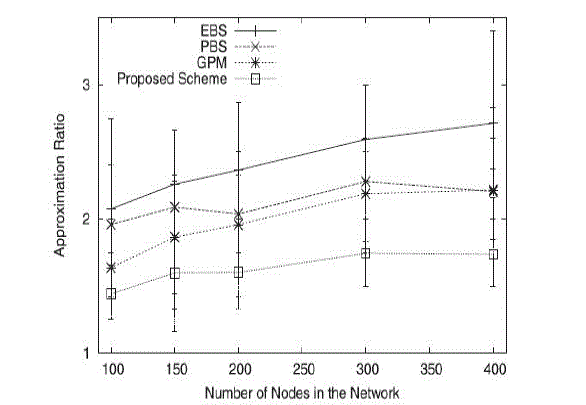
While we have experimented with various settings, we only report a set of representative results in the rest of this section. In Fig. 2, we present the average approximation ratios when we vary the number of nodes within a fixed-size square 1000 m _ 1000 m. Our proposed algorithm consistently outperforms existing schemes by 12-40 percent. Specifically, in the 400-node scenario, the average approximation ratio of our algorithm is 1.74, which is around 21 percent smaller than that of GPM (2.22) and PBS (2.21) and 40 percent smaller than that of EBS (2.92). Approximation ratio of our scheme goes up slightly, but the performance improvement over existing schemes is similar or larger.
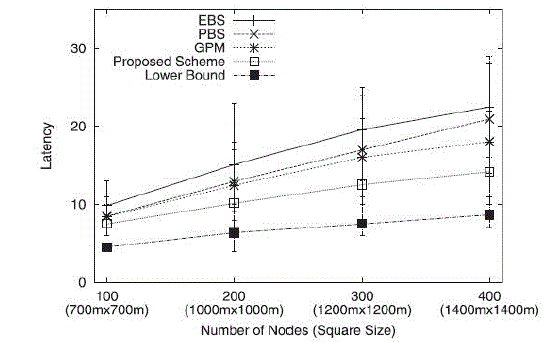
In Fig. 3, we present the average values of actual latency for broadcast algorithms as well as the height of BFS tree (i.e., lower bound). It varies both the number of nodes and the square size, so that the average number of neighbors is maintained similar. Observe that the proposed algorithm consistently outperforms existing schemes by 11-37 percent. D. Results for All-to-All Broadcast
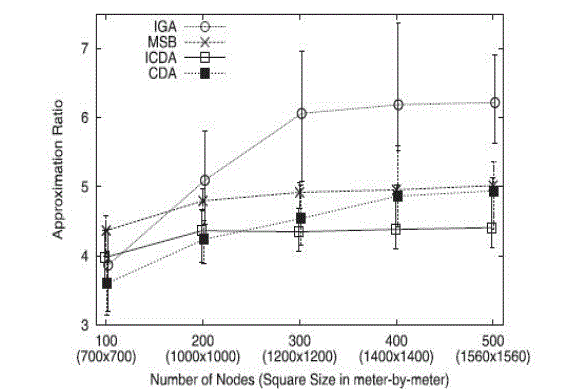
In Fig. 4, we present the average approximation ratio of our all-to-all broadcast schemes (CDA and ICDA), MSB and IGA that vary the number of nodes and the square size. Observe that the performance of CDA and ICDA in practice is much better than the analytical bound (20 and 34). CDA performs well when the network size is small However, the performance difference between CDA and MSB becomes smaller in larger Networks.

CONCLUSION
Thus an approximation algorithm for broadcasting in wireless networks was implemented. Our algorithm for ONE-TOALL BROADCASTING gives a 12-approximate Solution and the algorithms for ALL-TO-ALL BROADCASTING give approximation ratios of 20 and 34. But it is not enough for very large multihop networks, so in future it can be implemented for very large multihop networks in efficient manner to reduce latency and collision-free and to find the latency time in wireless networks.

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
 

References