Hashing function is the One of the most frequent way for finding the nearest match in the large data sets. From the last decades number of researcher has been work on the hashing and focusing on the better approach than the existing one with respective their performance. In this paper presents a survey on different type of hash functions, different type of hashing method, hashing strategies and structural weakness of them or the limitation of them that in which kind of problem they are suitable and what they can’t be used., also we are investigating the alternative approach for the mid- square hashing approach. The necessary data structures and algorithms are described, the expected performance is analyzed mathematically, and actual execution times are obtained and compared with alternative techniques. It shows that it provides the faster response time. Finally our method is intuitive and easy to implement.
Keywords |
| Hashing, algorithmic, access methods, data structures. |
INTRODUCTION |
| The address computation can be implemented in several ways in the hash table , here we discuss its basic operations
and typical hash function operations and the problem for which hash table are suitable and for which hash table are
not suitable. Focus on the some common hashing methods, folding methods and other hashing method Mid square,
Digit Addition, Analysis which are used in different application of Hashing. The necessary data structures and
algorithms are described, the expected performance is analyzed mathematically, and actual execution times are
obtained and compared with alternative techniques. |
| Hash defines “to hash” as “to chop up, as of potatoes”. This is exactly what hash functions usually do. A good hash
function creates disorder and, in this way, avoids collisions. |
OBJECTIVES |
| Finding the address of element from the hash table is one of the important task for performance of any algorithm.
This function can be done by Hash-fictions. |
| The some existing algorithms is complicated to implement and the constant of the space bound is large. With focus
of time and space bound ,We also study our opportunistic data structure in a dynamic setting and devise a variant
achieving effective search and update time bounds. The focus objective of this study is to reduce the computational
time of the Hashing function. Here we propose new algorithm as NKRSQR Hashing function with the following
objectives. |
| NKRSQR Algorithm should be easy to implement and easy to Understand. |
| NKRSQR Algorithm Must Return the result with minimum time complexity. |
RELATED WORK |
| Schmidt and Siegel [1] proposed the first algorithm for constructing a MPHF with constant evaluation time and
description size O(n + log log u) bits..From a practical point of view, the algorithm of Schmidt and Siegel is not
attractive. |
| The scheme is complicated to implement and the constant of the space bound is large. Ji, Jianqiu;Li, Jianmin et al [2]
introduce an effective method, i.e. the min-max hash method, which significantly reduces the hashing time by half, yet it has a provably slightly smaller variance in estimating pair wise Jaccard similarity. In addition, the estimator of minmax
hash only contains pair wise equality checking, thus it is especially suitable for approximate nearest neighbor
search. Experiments show that with the same length of hash code, min-max has reduces the hashing time to half as
much as that of min-wise hash. The divide-and-concatenate technique cannot speed up software implementations but
can only improve the collision probability beyond that provided by the processor architecture. This is because, if a
processor supports w-bit additions and multiplications in one or two cycles, then w/2-bit operations will also consume
the same number of cycles as w-bit operations.[2].Abutaha, M.Hamamreh, R.[3] Introduce The new one
way hash algorithm designed by using two steps. Firstly, convert the input data into matrix system by using all
necessary conversions to generate the initial hash value. Secondly, use the output of the first step to make a digest for
these data and finally generate the secure hash value. Joseph Gil and Yossi Matias implements the simple fast parallel
hashing by oblivious Execution. This algorithm was design with bucket approach in data structures . Experimental
result presents a simple fast and efficient parallel algorithm for the hashing problem Using n processors and the
running time of the algorithm is O(lg lg n). More recently, Hagerup and Tholey [4] have come up with the best
theoretical result we know of. The MPHF obtained can be evaluated in O(1) time and stored in n log e + log log u +
O(n(log log n)2/ log n + log log log u) bits. The construction time is O(n+log log u) using O(n) words of space. Again,
the terms involving u are negligible. In spite of its theoretical importance, the Hagerup and Tholey [4] algorithm is also
not practical, as it emphasizes asymptotic space complexity only. (It is also very complicated to implement. Hashingbased
approximate nearest neighbor (ANN) search in huge databases has become popular due to its computational and
memory efficiency[5]. |
PROPOSED ALGORITHM |
| From the literature review we can conclude that the well deep knowledge of different data structure allows us to
implement and design new algorithm which can fallow the basic principal of root data structure. The two principal
criteria use in selecting a hash function; |
| - It should be very easy and quick to compute. |
| - Function should, return value with minimum number of collisions. |
| and the next section also describes how address can be computed from the keys using the hash function. Several
variation on the basic theme are presented and analyzed; Focused line is that hashing is extremely effective and
practical technique. Question is that How easy is it to design a hash function? It is quite easy , as a little number
theory will help us prove. |
| A. Working Principal : |
| NKRSQR is based on the Divide and merge technique. This technique consist of decomposing the instance
and merge as individual element for problem solving. |
| Two questions that naturally spring to mind are: |
| 1.Why would any one want to do this? |
| 2.How should we solve ? |
| First we partition the number ‘n’ in ‘Two’ slots by taking the remainder of ‘n’.
That is the first step is computing as – |
| V1(n)= n mod 10--------------------eq(1) |
| V2(n)= n / 10--------------------------eq(2) |
| In second step apply the quadratic equation to find the square of number. Next Step can be done by extracting k bits
from the middle of the square of the key. |
| H(n)= (v1+v2)2 >>(w-n)----------------eq(3) |
| NKRSQR follows nature of recursive algorithm. This Algorithm does a pretty good job as compare to middle –square
method when the integer valued keys are equi-probable. |
| B. Address Space for Result Number: |
| The middle of square (or Mid- Square for short) function , fm is computed by squaring the identifiers and then using
an appropriate number of bits from middle of the square to obtain the bucket address.Since the middle bit of the
square will usually depend upon all of the characters’ in the identifier, it is expected that different identifiers would
result in different hash addresses with high probability even when some of the characters in the identifiers are the
same. |
| The number of bits to be used to obtain the bucket address depend on the table size . if n bits are used to compute
hash address, the range of value is 2n , so the size of hash table is chosen to be a power of 2 when this kind of scheme
is used . |
| MSHA(A)= n number of middle digits of (A2) |
| Where, |
| MSHA=Mid Square Hash Address |
NKRSQR ADVANTAGES AND DISADVANTAGES |
| As earlier we note the phrase of universe , now we will discusses the some advantages and disadvantages of
NKRSQR Hash function, This algorithm run faster than the existing one. However this is limited upto number 99
only. |
NKRSQR RESULTS |
| The proposed energy efficient algorithm is implemented with basic programming of Algorithm. We tested output
result with numbers from 1 to 99 for different size and required time . Proposed algorithm is compared with the basic
traditional Mid-square hash function for address mapping . We considered the time and memory space , and
processor execution time is calculated through the CPUTIME function of the program . proposed algorithm provides
better complexity with respective time and space which is a need of computer era for speedup the process and
maximum storage. |
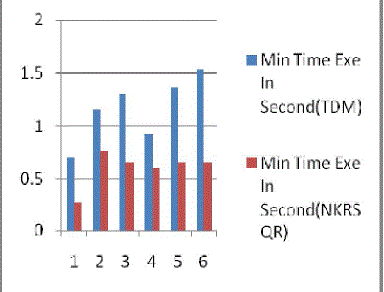
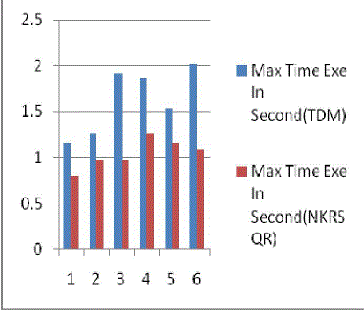
| The result Fig. 1 shows the Traditional Vs New(NKRSQR) approach for min time. In the same way Fig 2 shows
Traditional Vs New(NKRSQR) approach for Max time. Table 1. shows the Result Using Traditional Method of Time
and memory usage while Table 2 shows Result Using (NKRSQR) Method , which defines the better execution time. |
| The results shows in Fig 1 of Traditional Vs New(NKRSQR) approach for min time ,that the proposed algorithm
performs better with the minimum running time of this implementation is much less than the the traditional Midsquare
hash function. |
| The results shows in Fig 2 of Traditional Vs New(NKRSQR) approach for Max time ,that the proposed algorithm
performs better with the Maximum running time of this implementation is much less than the the traditional Midsquare
hash function. |
| The Table 1 shows the Minimum and maximum time required time for Traditional approach of hash squring
method . |
| The Table 2 shows the Minimum and maximum time required time for NKRSQR approach of hash squring
method . |
CONCLUSION AND FUTURE WORK |
| The results showed that the proposed algorithm performs better with the running time of this implementation is
much less than the the traditional Mid- square hash function. The proposed algorithm provides better complexity with
respective time and space which is a need of computer era for speedup the process and maximum storage. As the
performance of the proposed algorithm is analyzed with only traditional Mid- square approach in hashing functions in
future with some modifications in design considerations the performance of the proposed algorithm can be compared
with other efficient algorithm. NKRSQR is the simplest hash function which is obtain by combination of two
different method that is Division hash function and squaring hash function. |
Tables at a glance |
 |
 |
| Table 1 |
Table 2 |
|
| |
Figures at a glance |
 |
 |
| Figure 1 |
Figure 2 |
|
| |
References |
- Singh, M.; Garg, D., "Choosing Best Hashing Strategies and Hash Functions," Advance Computing Conference, 2009. IACC 2009. IEEEInternational , vol., no., pp.50,55, 6-7 March 2009 doi: 10.1109/IADCC.2009.4808979
- Bo Yang; Karri, R.; McGrew, D.A., "Divide-and-concatenate: an architecture-level optimization technique for universal hashfunctions," Computer-Aided Design of Integrated Circuits and Systems, IEEE Transactions on , vol.24, no.11, pp.1740,1747, Nov. 2005 doi: 10.1109/TCAD.2005.852455
- Abutaha, M.; Hamamreh, R., "New one way hash algorithm using non-invertible matrix," Computer Medical Applications (ICCMA),2013 International Conference on , vol., no., pp.1,5, 20-22 Jan. 2013 doi: 10.1109/ICCMA.2013.6506174
- T. Hagerup and T. Tholey. Efficient minimal perfect hashing in nearly minimal space. In Proc. of the 18th Symposium on TheoreticalAspects of Computer Science (STACS’01), pages 317–326. Springer LNCS vol. 2010, 2001.
- Jun Wang; Kumar, S.; Shih-Fu Chang, "Semi-Supervised Hashing for Large-Scale Search," Pattern Analysis and Machine Intelligence,IEEE Transactions on , vol.34, no.12, pp.2393,2406, Dec. 2012 doi: 10.1109/TPAMI.2012.48.
- Kollios, G.; Tsotras, V.J., "Hashing methods for temporal data," Knowledge and Data Engineering, IEEE Transactions on , vol.14, no.4,pp.902,919, Jul/Aug 2002 doi: 10.1109/TKDE.2002.1019221
- Jae-PilHeo; Youngwoon Lee; Junfeng He; Shih-Fu Chang; Sung-Eui Yoon, "Spherical hashing," Computer Vision and PatternRecognition (CVPR), 2012 IEEE Conference on , vol., no., pp.2957,2964, 16-21 June 2012 doi: 10.1109/CVPR.2012.6248024
- FengYue; Bin Li; Ming Yu; Jiaqiang Wang, "Hashing Based Fast Palmprint Identification for Large-Scale Databases," InformationForensics and Security, IEEE Transactions on , vol.8, no.5, pp.769,778, May 2013 doi: 10.1109/TIFS.2013.2253321
- Ye-In Chang; Chien-I Lee; Wann-Bay ChangLiaw, "Linear spiral hashing for expansible files," Knowledge and Data Engineering, IEEETransactions on , vol.11, no.6, pp.969,984, Nov/Dec 1999 doi: 10.1109/69.824617.
- Minho Jin; Yoo, C.D., "Quantum Hashing for Multimedia," Information Forensics and Security, IEEE Transactions on , vol.4, no.4,pp.982,994, Dec. 2009 doi: 10.1109/TIFS.2009.2033221
- Yuenan Li; Zheming Lu; Ce Zhu; XiaMuNiu, "Robust Image Hashing Based on Random Gabor Filtering and Dithered Lattice VectorQuantization," Image Processing, IEEE Transactions on , vol.21, no.4, pp.1963,1980, April 2012 doi: 10.1109/TIP.2011.2171698
- Lamberger, M.; Pramstaller, N.; Rechberger, C.; Rijmen, V., "Analysis of the Hash Function Design Strategy Called SMASH,"Information Theory, IEEE Transactions on , vol.54, no.8, pp.3647,3655, Aug. 2008 doi: 10.1109/TIT.2008.926420
- Gordon, D.M.; Miller, V.S.; Ostapenko, P., "Optimal Hash Functions for Approximate Matches on the -Cube," Information Theory, IEEETransactions on , vol.56, no.3, pp.984,991, March 2010 doi: 10.1109/TIT.2009.2039037.
- Jin, Z.; Li, C.; Lin, Y.; Cai, D., "Density Sensitive Hashing," Cybernetics, IEEE Transactions on , vol.PP, no.99, pp.1,1,0doi: 10.1109/TCYB.2013.2283497.
|