International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Efficient Multi-dimensional Fuzzy Search for Personal Information Management Systems

DR.K.P.KALIYAMURTHIE1 AND D.PARAMESWARI2
  1. Professor and Head, Dept. of IT, Bharath University, Chennai-600 073
  2. Asst. Prof. (SG), Dept. of Computer Applications, Jerusalem College of Engg., Chennai-600 100
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

With the explosion in the amount of semi-structured data users access and store in personal information management systems, there is a critical need for powerful search tools to retrieve often very heterogeneous data in a simple and efficient way. Existing tools typically support some IR-style ranking on the textual part of the query, but only consider structure (e.g., file directory) and metadata (e.g., date, file type) as filtering conditions. We propose a novel multi-dimensional search approach that allows users to perform fuzzy searches for structure and metadata conditions in addition to keyword conditions. Our techniques individually score each dimension and integrate the three dimension scores into a meaningful unified score. We also design indexes and algorithms to efficiently identify the most relevant files that match multi-dimensional queries. We perform a thorough experimental evaluation of our approach and show that our relaxation and scoring framework for fuzzy query conditions in non content dimensions can significantly improve ranking accuracy. We also show that our query processing strategies perform and scale well, making our fuzzy search approach practical for every day usage.

INTRODUCTION
THE amount of data stored in personal information management systems is rapidly increasing, following therelentless growth in capacity and dropping price of storage. This explosion of information is driving a critical need for powerful search tools to access often very heterogeneous data in a simple and efficient manner. Such tools should provide both high-quality scoring mechanisms and efficient query processing capabilities. Numerous search tools have been developed to perform keyword searches and locate personal information stored in file systems, such as the commercial tools Google Desktop Search and Spotlight . However, these tools usually support some form of ranking for the textual part of the query—similar to what has been done in the Information Retrieval (IR) community—but only consider structure (e.g., file directory) and metadata (e.g., date, file type) as filtering conditions. Recently, the research community has turned its focus on search over to Personal Information and Dataspaces , which consist of heterogeneous data collections. However, as is the case with commercial file system search tools, these works focus on IR-style keyword queries and use other system information only to guide the keyword-based search. Keyword-only searches are often insufficient, as illustrated by the following example:
Example 1: Consider a user saving personal information in the file system of a personal computing device. In addition to the actual file content, structural location information (e.g., directory structure) and a potentially large amount of metadata information (e.g., access time, file type) are also stored by the file system.
In such a scenario, the user might want to ask the query:
[filetype = *.doc AND
createdDate = 03/21/2007 AND
content = “proposal draft” AND
structure = /docs/Wayfinder/proposals]
Current tools would answer this query by returning all files of type *.doc created on 03/21/2007 under the directory /docs/Wayfinder/proposals (filtering conditions) that have content similar to “proposal draft” (ranking expression), ranked based on how close the content matches“proposal draft” using some underlying text scoring mechanism.
Because all information other than content are used only as filtering conditions, files that are very relevant to the query, but which do not satisfy these exact conditions would be ignored. We argue that allowing flexible conditions on structure and metadata can significantly increase the quality and usefulness of search results in many search scenarios. For instance, in Example 1, the user might not remember the exact creation date of the file of interest but remembers that it was created around 03/21/2007. Similarly, the user might be primarily interested in files of type *.doc but might also want to consider relevant files of different but related types(e.g., *.tex or *.txt). Finally, the user might misremember the directory path under which the file was stored. In this case, by using the date, size, and structure conditions not as filtering conditions but as part of the ranking conditions of the query.Once a good scoring mechanism is chosen, efficient algorithms to identify the best query results, without considering all the data in the system, are also needed. In this paper, we propose a novel approach that allows users to efficiently perform fuzzy searches across three different dimensions: content, metadata, and structure. We describe individual IDF-based scoring approaches for each dimension and present a unified scoring framework for multi-dimensional queries over personal information file systems. We also present new data structures and index construction optimizations to make finding and scoring fuzzy matches efficient.
Our specific contributions1 include:
• We propose IDF-based scoring mechanisms for content, metadata, and structure, and a framework to combine individual dimension scores into a unified
multi-dimensional score (Section 2).
• We adapt existing top-k query processing algorithms and propose optimizations to improve access to the structure dimension index. Our optimizations take into account the top-k evaluation strategy to focus on building only the parts of the index that are most relevant to the query processing (Sections 3 and 4).
• We evaluate our scoring framework experimentally and show that our approach has the potential to significantly improve search accuracy over current filtering approaches (Sections 5.2 and 5.3).
• We empirically demonstrate the effect of our optimizations on query processing time and show that our optimizations drastically improve query efficiency and result in good scalability (Sections 5.4∼5.8). There has been discussions in both the Database and
IR communities on integrating technologies from the two fields [1], [2], [7], [12] to combine content-only searches with structure-based query results. Our techniques provide a step in this direction as they integrate IR-style content scores with DB-style structure approximation scores. The rest of the paper is organized as follows. In Section 2, we present our multi-dimensional scoring framework. In Section 3, we discuss our choice of top-k query processing algorithm and present our novel static indexing 1. This work builds upon and significantly expands our work on scoring multi-dimensional data [24]. The top-k query processing indexes and algorithms of Sections 3 and 4 are novel contributions as are the experimental results of Sections 5.4∼5.8. structures and score evaluation techniques. Section 4 describes dynamic indexing structures and index construction algorithms for structural relaxations. In Section 5, we present our experimental results. Finally, conclude in Section 6.

UNIFIED MULTI-DIMENSIONAL SCORING
In this section, we present our unified framework for assigning scores to files based on how closely they match query conditions within different query dimensions. We distinguish three scoring dimensions: content for conditions on the textual content of the files, metadata for conditions on the system information related to the files, and structure for conditions on the directory path to access the file. We represent files and their associated metadata and structure information as XML documents. Scores across multiple dimensions are unified into a single overall score for ranking of answers. Our scoring strategy is based on an IDF-based interpretation of scores, as described below. For each query condition, we score files based on the least relaxed form of the condition that each file matches. Scoring along all dimensions is uniformly IDF-basedwhich permits us to meaningfully aggregate multiple singledimensional scores into a unified multi-dimensional score.

Scoring Content
We use standard IR relaxation and scoring techniques for content query conditions [30]. Specifically, we adopt the TF·IDF scoring formulas from Lucene [6], a state-of-theart keyword search tool. These formulas are as follows:
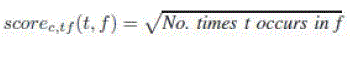equation (1)
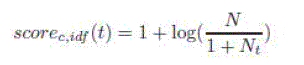equation (2)
equation (3)
where Q is the content query condition, f is the file being scored, N is the total number of files, Nt is the number of files containing the term t, and NormLength(f) is a normalizing factor that is a function of f’s length. 2 Note that relaxation is an integral part of the above formulas since they score all files that contain a subset of the terms in the query condition.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication.

Scoring Metadata
We introduce a hierarchical relaxation approach for each type of searchable metadata to support scoring. For example,Figure 1 shows (a portion of) the relaxation levels for file types, represented as a DAG3. Each leaf represents a specific file type (e.g., pdf files). Each internal node represents a more general file type that is the union of the types of its children (e.g., Media is the union of Video, Image,and Music) and thus is a relaxation of its descendants.
A key characteristic of this hierarchical representation is containment; that is, the set of files matching a node must be equal to or subsume the set of files matching each of its children nodes. This ensures that the score of a file matching a more relaxed form of a query condition is always less than or equal to the score of a file matching a less relaxed form (see Equation 4 below). We then say that a metadata condition matches a DAG node if the node’s range of metadata values is equal to or subsumes the query condition. For example, a file type query condition specifying a file of type “*.cpp” would match the nodes representing files of type “Code”,files of type “Document”, etc. A query condition on the creation date of a file would match different levels of time granularity, e.g., day, week or month. The nodes on the path from the deepest (most restrictive) matching node to the root of the DAG then represent all of the relaxations that we can score for that query condition. Similarly, each file matches all nodes in the DAG that is equal to or subsumes the file’s metadata value. Finally, given a query Q containing a single metadata condition M, the metadata score of a file f with respect to Q is computed as:
equation (4)
where N is the total number of files, nM is the deepest node that matches M, nf is the deepest DAG node that matches f, commonAnc(x, y) returns the closest common ancestor of nodes x and y in the relaxation hierarchy, and nFiles(x) returns the number of files that match node x. The score is normalized by log(N) so that a single perfect match would have the highest possible score of 1.2.

Scoring Structure
Most users use a hierarchical directory structure to organize their files. When searching for a particular file, a user may often remember some of the components of the containing directory path and their approximate ordering rather the exact path itself. Thus, allowing for some approximation on structure query conditions is desirable because it allows users to leverage their partial memory to help the search engine locate the desired file. Our structure scoring strategy extends priorwork on XML structural query relaxations [4], [5]. Specifically, the node inversion relaxation introduced below is novel and introduced to handle possible misordering of path name components when specifying structure query conditions in personal file systems. Assuming that structure query conditions are given as non-cyclic paths (i.e., path queries), these relaxations are:
• Edge Generalization is used to relax a parent-child relationship to an ancestor-descendant relationship.For example, applying edge generalization to /a/b would result in /a//b.
• Path Extension is used to extend a path P such that all files within the directory subtree rooted at P can be considered as answers. For example, applying path extension to /a/b would result in /a/b//∗.
• Node Inversion is used to permute nodes within a path query P. To represent possible permutations, we introduce the notion of node group as a path where the placement of edges are fixed and (labeled) nodes may permute. Permutations can be applied to any adjacent nodes or node groups except for the root and ∗ nodes. A permutation combines adjacent nodes, or node groups, into a single node group while preserving the relative order of edges in P. For example, applying node inversion on b and c from /a/b/c would result in /a/(b/c), allowing for both the original query condition as well as /a/c/b. The (b/c) part of the relaxed condition /a/(b/c) is called a node group.
• Node Deletion is used to drop a node from a path. Node deletion can be applied to any path query or node group but cannot be used to delete the root node or the ∗ node.To delete a node n in a path query P: – If n is a leaf node, n is dropped from P andP − n is extended with //∗. This is to ensure containment of the exact answers to P in the set of answers to P _, and monotonicity of scores.– If n is an internal node, n is dropped from P and parent(n) and child(n) are connected in P with //.
For example, deleting node c from a/b/c results in a/b//∗ because a/b//∗ is the most specific relaxed path query containing a/b/c that does not contain c. Similarly, deleting c from a/c/b//∗ results in a//b//∗.To delete a node n that is within a node group N This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication.
Fig. 2. Structure relaxation DAG. Solid lines represent parent-child relationships. Dotted linesrepresentancestordescendant relationships, with intermediate nodes removed for simplicity of presentation. IDF scores are shown at the top right corner of each DAG node. in a path query P, the following steps are required to ensure answer containment and monotonicity of scores:
– n and one of its adjacent edge in N are dropped from N. Every edge within N becomes an ancestor-descendant edge. If n is the only node left in N, N is replaced by that node in P.
– Within P the surrounding edges of N are replaced by ancestor-descendant edges.
– If N is a leaf node group, the result query is extended with //∗.

Score Aggregation
We aggregate the above single-dimensional scores into a unified multi-dimensional score to provide a unified ranking of files relevant to a multi-dimensional query. To do this, we construct a query vector, V_Q, having a value of 1 (exact match) for each dimension and a file vector, V_F , consisting of the single-dimensional scores of file F with respect to query Q. (Scores for the content dimension is normalized against the highest score for that query condition to get values in the range [0, 1].) We then compute the projection of V_F onto V_Q and the length of the resulting vector is used as the aggregated score of file F. In its current form, this is simply a linear combination of the component scores with equal weighting. The vector projection method, however, provides a framework for future exploration of more complex aggregations.

QUERY PROCESSING
We adapt an existing algorithm called the Threshold Algorithm (TA) [15] to drive query processing. TA uses a threshold condition to avoid evaluating all possible matchesto a query, focusing instead on identifying the k best answers. It takes as input several sorted lists, each containing the system’s objects (files in our scenario) sorted in descending order according to their relevance scores for a particular attribute (dimension in our scenario), and This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. dynamically accesses the sorted lists until the threshold condition is met to find the k best answers. Critically, TA relies on sorted and random accesses to retrieve individual attribute scores. Sorted accesses, that is, accesses to the sorted lists mentioned above, require the files to be returned in descending order of their scores for a particular dimension. Random accesses require the computation of a score for a particular dimension for any given file.

Evaluating Content Scores
As mentioned in Section 2.1, we use existing TF·IDF methods to score the content dimension. Random accesses are supported via standard inverted list implementations, where, for each query term, we can easily look up the term frequency in the entire file system as well as in a particular file. We support sorted accesses by keeping the inverted lists in sorted order; that is, for the set of files that contain a particular term, we keep the files in sorted order according to their TF scores, normalized by file size, for that term.4 We then use the TA algorithm recursively to return files in sorted order according to their content scores for queries that contain more than one term.

Evaluating Metadata Scores
Sorted access for a metadata condition is implemented using the appropriate relaxation DAG index. First, exact matches are identified by identifying the deepest DAG node N that matches the given metadata condition (see Section 2.2). Once all exact matches have been retrieved from N’s leaf descendants, approximate matches are produced by traversing up the DAG to consider more approximate matches. Each parent contains a larger range of values than its children, which ensures that the matches are returned in decreasing order of metadata scores. Similar to the content dimension, we use the TA algorithm recursively to return files in sorted order for queries that contain multiple metadata conditions. Random accesses for a metadata condition require locating in the appropriate DAG index the closest common ancestor of the deepest node that matches the condition and the deepest node that matches the file’s metadata attribute (see Section 2.2). This is implemented as an efficient DAG traversal algorithm.

Evaluating Structure Scores
The structure score of a file for a query condition depends on how close the directory in which the file is stored 4. This gives the same sorted order as TF·IDF since the IDF score of a term is the same for all files.
Fig. 3. A directory tree and its structure index. matches the condition. All files within the same directory will therefore have the same structure score. To compute the structure score of a file f in a directory d that matches the (exact or relaxed) structure condition P of a given query, we first have to identify all the directory paths, including d, that match P. For the rest of the section, we will use structure condition to refer to the original condition of a particular query and query path to refer to a possibly relaxed form of the original condition. We then sum the number of files contained in all the directories matching P to compute the structure score of these files for the query using Equation 6. The score computation step itself is straightforward; the complexity resides in the directory matching step. Node inversions complicate matching query paths with directories, as all possible permutations have to be considered. Specific techniques and their supporting index structures need to be developed.Several techniques for XML query processing have focused on path matching. Most notably, the PathStack algorithm [9] iterates through possible matches using stacks, each corresponding to a query path component in a fixed order. To match a query path that allows permutations (because of node inversion) for some of its components, we need to consider all possible permutations of these components (and their corresponding stacks) and a directory match for a node group may start and end with any one of the node group components, which makes it complicated to adapt the PathStack approach to our scenario. We use a two-phase algorithm to identify all directories that match a query path. First, we identify a set of candidate directories using the observation that for a directory d to match a query path P, it is necessary for all the components in P to appear in d. For example, the directory /docs/proposals/final/Wayfinder is a potential match for the query path /docs/(Wayfinder//proposals) since the directory contains all three components docs, Wayfinder, and proposals. We implement an inverted index mapping components to directories to support this step (see Figure 3). We extend our index to maintain the position that each component appears within each directory (Figure 3). For efficiency, each directory is represented by an integer directory id, so that each entry in the index is a pair of integers (DirID, position). This augmented index This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. allows us to quickly check structural relationships between components of a directory

OPTIMIZING QUERY PROCESSING IN THE STRUCTURE DIMENSION
In this section, we present our dynamic indexes and algorithms for efficient processing of query conditions in the structure dimension. This dimension brings the following challenges:
• The DAGs representing relaxations of structure conditions [4], [24] are query-dependent and so have to be built at query processing time. However, since these DAGs grow exponentially with query size, i.e., the number of components in the query, efficient index building and traversal techniques are critical issues.
• The TA algorithm requires efficient sorted and random access to the single-dimension scores (Section 3). In particular, random accesses can be very expensive. We need efficient indexes and traversal algorithms that support both types of access. We propose the following techniques and algorithms to address the above challenges. We incrementally build the query dependent DAG structures at query time, only materializing those DAG nodes necessary to answer a query (Section 4.1). To improve sorted access efficiency, we propose techniques to skip the scoring of unneeded DAG nodes by taking advantage of the containment property of the DAG (Section 4.2). We improve random accesses using a novel algorithm that efficiently locates and evaluates only the parts of the DAG that match the file requested by each random access (Section 4.3).

Incremental Identification of Relaxed Matches
As mentioned in Section 2.3, we represent all possible relaxations of a query condition and corresponding IDF scores using a DAG structure. Scoring an entire query relaxation DAG can be expensive as they grow exponentially with the size of the query condition. For example, there are 5, 21, 94, 427, and 1946 nodes in the respective complete DAGs for query conditions /a, /a/b, /a/b/c, /a/b/c/d,/a/b/c/d/e. However, in many cases, enough query matches will be found near the top of the DAG, and a large portion of the DAG will not need to be scored. Thus, we use a lazy evaluation approach to incrementally build the DAG, expanding and scoring DAG nodes to produce additional matches when needed in a greedy fashion [29]. The partial evaluation should nevertheless ensures that directories (and therefore files) are returned in the order of their scores. For a simple top-k evaluation on the structure condition, our lazy DAG building algorithm is applied and stops when k matches are identified. For complex queries involving multiple dimensions, the algorithm can be used for sorted This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. access to the structure condition. Random accesses are more problematic as they may access any node in the DAG. The DAG building algorithm can be used for random access, but any random access may lead to the materialization and scoring of a large part of the DAG.5 In the next sections we will discuss techniques to optimize sorted and random access to the query relaxation DAG.

Improving Sorted Accesses
Evaluating queries with structure conditions using the lazy DAG building algorithm can lead to significant query evaluation times as it is common for multi-dimensional topk processing to access very relaxed structure matches, i.e., matches to relaxed query paths that lay at the bottom of the DAG, to compute the top-k answers. An interesting observation is that not every possible relaxation leads to the discovery of new matches. For example, in Figure 2, the query paths /docs/Wayfinder/proposals,//docs/Wayfinder/proposals, and//docs//Wayfinder/proposals have exactly the same scores of 1, which means that no additional files were retrieved after relaxing /docs/Wayfinder/proposals to either//docs/Wayfinder/proposals or//docs//Wayfinder/proposals (Equation 6). By extension, if two DAG nodes share the same score, then all the nodes in the paths between the two DAG nodes must share the same score as well per the DAG definition. This is formalized in Theorem 1

Improving Random Accesses
Top-k query processing requires random accesses to the DAG. Using sorted access to emulate random access tends to be very inefficient as it is likely the top-k algorithm will access a file that is in a directory that only matches a very relaxed version of the structure condition, resulting in most of the DAG being materialized and scored. While the DAGJump algorithm somewhat alleviates this problem by reducing the number of nodes that need to be scored, efficient random access remains a critical problem for efficient top-k evaluations. We present the RandomDAG algorithm (Algorithm 2) to optimize random accesses over our structure DAG. The key idea behind RandomDAG is to skip to a node P in the DAG that is either a close ancestor of the actual least relaxed node P_ that matches the random access file’s parent (containing) directory d or P _ itself and only materialize and score the sub-DAG rooted at P as necessary to score P _. The intuition is that we can identify P by comparing d and the original query condition. In particular, we compute the intersection between the query condition’s components and d. P is then computed by dropping all components in the query condition that is not in the intersection, replacing parent-child with ancestor-descendant relationships as necessary. The computed P is then guaranteed to be equal to or an ancestor of P _. As DAG nodes are scored, the score together with matching directories are cached to speed up future random accesses. As an example, for our query condition /docs/Wayfinder/proposals in Figure 2, if the top-k algorithm wants to perform a random access to evaluate the structure score of a file that is in the directory /archive/proposals/Planetp,RandomDAGwill first compute the close ancestor to the node that matches /archive/proposals/Planetp as the intersection between the query condition and the file directory, i.e., //proposals, and will jump to the sub-DAG rooted at this node. The file’s directory does not match this query path, but does match its child //proposals//* with a structure score of 0.197. This
Fig. 5. An example execution of RandomDAG that returns the score of a file that is in the directory /archive/proposals/Planetp for the query condition /docs/Wayfinder/proposals. is illustrated in Figure 5 which shows the parts of the DAG from Figure 2 that would need to be accessed for a random access to the score of a file that is in the directory /archive/proposals/Planetp.

EXPERIMENTAL RESULTS
We now experimentally evaluate the potential for our multidimensional fuzzy search approach to improve relevance ranking. We also report on search performance achievable using our indexing structures, scoring algorithms, and top-k adaptation.

Impact of Flexible Multi-Dimensional Search
We begin by exploring the potential of our approach to improve scoring (and so ranking) accuracy using two example search scenarios. In each scenario, we initially construct a content-only query intended to retrieve a specific target file and then expand this query along several other dimensions. For each query, we consider the ranking of the target file by our approach together with whether the target file would be ranked at all by today’s typical filtering approaches on non-content query conditions.
A representative sample of results is given in Table 1. In the first example, the target file is the novel “The Time Machine” by H. G. Wells, located in the directory path /Personal/Ebooks/Novels/, and the set of query content terms in our initial content-only query Q1 contains the two terms time and machine. While the query is quite reasonable, the terms are generic enough that they appear in many files, leading to a ranking of 18 for the target file. Query Q2 augments Q1 with the exact matching values for file type, modification date, and containing directory. This brings the rank of the target file to 1. The remaining queries explore what happens when we provide an incorrect value for the non-content dimensions. For example, in query Q10,a couple of correct but wrongly ordered components in the directory name still brings the ranking up to 1. In contrast, if such directories were given as filtering conditions, the target file would be considered irrelevant to the query and not ranked at all; queries which contain a “*” next to our technique’s rank result represent those in which the target file would not be considered as a relevant answer given today’s typical filtering approach. Results for the second example, which is a search for an email, are similar. This study also presents an opportunity for gauging the potential impact of the node inversion relaxation. Specifically, queries Q23 and Q26 in the second example misorder the structure conditions as /Java/Mail and /Java/Code, respectively, compared to the real pathname /Personal/Mail/Code/Java. Node inversion allow these conditions to be relaxed to //(Java//Mail) and //(Java//Code), so that the target file is still ranked 1. Without node inversion, these conditions cannot match the target until they both are relaxed to //Java/*, the matching relaxation with the highest IDF score, using node deletion. This leads to ranks of 9 and 21 since files under other directories such as /Backup/CodeSnippet/Java and /workspace/BookExample/Java now have the same structure scores as the target file. In another example scenario not shown here, a user is searching for the file wayfinder cons.ppt stored in the directory /Personal/publications/wayfinder/presentations. The query with content condition wayfinder, 8. Content was extracted from MP3 music files using their ID3 tags. availability, paper and structure condition /Personal/wayfinder/presentations would rank wayfinder cons.ppt 1. However, if the structure condition is misordered as /Personal/presentations/wayfinder or /presentations/Personal/wayfinder, the rank of the target file would fall to 17 and 28, respectively, without node inversion. With node inversion, the conditions are relaxed to /Personal//(presentations/wayfinder) and /(presentations//Personal/wayfinder), respectively, and the target file is still ranked 1.
Base Case Query Processing Performance
We now turn to evaluating the search performance of our system. Content may change prior to final publication.
the base case where the system constructs and evaluates a structural DAG sequentially without incorporating the DAGJump (Section 4.2) and RandomDAG (Section 4.3) optimization algorithms. Note that the base case still includes the implementation of the matchDirectory (Section 3.3) and incremental DAG building (Section 4.1) techniques.

Query Processing Performance with Optimizations
Figure 7(b) gives the query processing times for the same 15 queries shown in Figure 7(a), but after we have applied both the DAGJump and the RandomDAG algorithms. We observe that these optimizations significantly reduce the query processing times for most of these queries. In particular, the query processing time of the slowest query, Q10, decreased from 125.57 to 1.96 seconds. Although not shown here, all 80 queries now require at most 0.39 seconds of processing time for the structure dimension, This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication.

CONCLUSIONS
We presented a scoring framework for multi-dimensional queries over personal information management systems. Specifically, we defined structure and metadata relaxations and proposed IDF-based scoring approaches for content, metadata, and structure query conditions. This uniformity of scoring allows individual dimension scores to be easily aggregated. We have also designed indexing structures and dynamic index construction and query processing optimizations to support efficient evaluation of multi-dimensional queries. We implemented and evaluated our scoring framework and query processing techniques. Our evaluation show that our multi-dimensional score aggregation technique preserves the properties of individual dimension scores and has the potential to significantly improve ranking accuracy. We also show that our indexes and optimizations are necessary to make multidimensional searches efficient enough for practical everyday usage. Our optimized query processing strategies exhibit good behavior across all dimensions, resulting in good overall query performance and scalability.

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3
Figure 5 Figure 6 Figure 7
 

References