Enactment of Offline and Online Mode
Mapping In Computational Grids

D. Thilagavathi; Dr. Antony Selvadoss Thanamani

Enactment of Offline and Online Mode Mapping In Computational Grids

D. Thilagavathi, Dr. Antony Selvadoss Thanamani

Ph D, Research Scholar, Department of Computer Science, NGM College, Pollachi, India
Associate Professor and Head, Department of Computer Science, NGM College, Pollachi, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

A Grid environment provides computational power to solve a hard problem, which otherwise might take a very large amount of time to execute on a single machine. Since the resources are physically scattered and diverse in nature, the algorithm used to assign the resources to jobs plays a significant role in the competence of the Grid scheduler. The major goal of Grid scheduler is to allocate each job to a resource, in such a way that the total time taken to execute all the jobs and their makespan, flowtime, tardiness are minimized. Thereby the resource utilization in grid is maximized. This job scheduling problem is known to be NP-Complete. This paper examines the four deterministic scheduling algorithms like Min-Min, Max-Min, Minimum Completion Time and Minimum Execution Time.

Keywords

Grid scheduler, Makespan, Flowtime, Tardiness, NP-Complete.

INTRODUCTION

A ‘Grid’ is a collection of different machines where in all of them contribute any combination of resources as an entire unit. The basic aim of Grid Computing is to create an illusion of a large and powerful virtual computer which is a collection of heterogeneous systems. ‘Grid’ Computing focuses on sharing of large scale of resources which are virtual to us. Systems connected in a grid can be inexpensive and located world-wide, as opposed to High-End computing [1]. It enables an application to run on a different machine, whose existing machine may be busy.

Grid scheduling is a process responsible for assigning users jobs onto available Grid resources. The goal of this process is to maximize various optimization criteria such as machine usage, fairness or to guarantee non trivial QoS (Quality of Service). Scheduling process should be flexible and fast so that it is able to efficiently react on dynamic changes in the Grid environment (job arrival, failure, imprecise job runtime estimate, etc.).

Effective scheduling in the Grid environment is a complex problem which is not fully and efficiently solved in nowadays production systems. Finding of optimal solution is an NP complete problem which is practically intractable for larger sets of jobs. The basic work of a Scheduler in grid environment is to automatically select a suitable machine to execute a particular job send by the Grid System. Examples are like Nimrod-G Grid Resource Broker, AppleS, STORM, Silver Meta scheduler, ST-ORM, CONDOR-G.

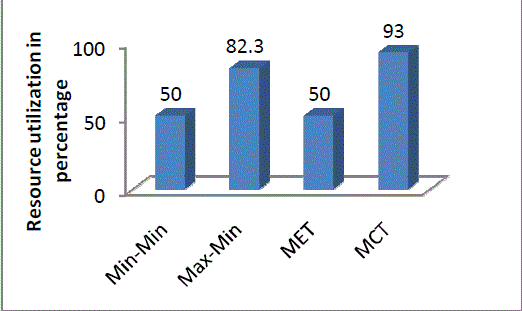
In this paper, solving scheduling problem in grid environment is studied using four scheduling algorithms like Min- Min, Max-Min, Minimum Completion Time(MCT) and Minimum Execution Time(MET) in which the optimization criteria’s like makespan, flowtime and tardiness are evaluated. The ultimate goal of scheduling is to achieve maximum resource utilization.

The rest of the paper is organized as follows. Section II discusses about the related work done by other researchers in grid scheduling problem. Section III gives the problem statement. Section IV briefs about the four static grid scheduling algorithms. Section V outlines the results of our experimental study and finally the paper conclusion is given in Section VI.

RELATED WORK

Optimal resource selection for jobs is known to be NP-Complete problem. Since complete search for solution would often fail, extensive research has been done, and numerous algorithms have been proposed and studied in literature [2][3][4]. They can be classified broadly into two categories, namely deterministic and meta-heuristics. The deterministic class of algorithms includes Min-Min, Max-Min, Suffrage, etc.

In paper [5], the author addresses a new scheduling algorithm called RASA. Here it takes advantages of MINMIN and MAX-MIN algorithm and tries to avoid their drawbacks. The algorithm builds a matrix C where Cij represents the completion time of the task Ti on the resource Rj. If the number of available resources is odd, the Min-min strategy is applied to assign the first task, otherwise the Max-min strategy is applied. The remaining tasks are assigned to their appropriate resources by one of the two strategies, alternatively. Min-min and Max-min algorithms are applicable in small scale distributed systems. Whereas RASA can be applied to large scale distributed systems.

The meta-heuristics class of algorithms includes Tabu Search [6], Ant Algorithm [7], Particle Swarm Optimization [8], Simulated Annealing [9], Genetic Algorithm [10] and Intelligent Water Drop Algorithm [11]. These are stochastic in nature.

Initially, the meta-heuristics classes of algorithms randomly generate population of potential solutions. In subsequent iterations, certain predefined operations are performed, in search of optimal or near-optimal solutions. The algorithms terminate when the solutions satisfy the fitness criterion, which is used to evaluate the candidate solutions.

PROBLEM STATEMENT

Consider there are n jobs and m resources in the grid environment. Then our job scheduling challenge is to find the best or optimal resources. The major objective functions to assess a Grid scheduler performance are Makespan, Flowtime and Tardiness [13]. Makespan is the time difference between the start time of the first task and the finish time of the last task [12]. We can also treat it as turnaround time in which the time gap between submissions of first task and completion of end task. Actually Makespan is a measure of the throughput of the heterogeneous computing system.

Let task set T = t1, t2, t3, …, tn be the group of tasks submitted to scheduler and Let Resource set R = r1, r2, r3, …, rm be the set of resources available at the time of task arrival makespan produced by any algorithm for a schedule can be calculated as follows:

(1) makespan = max(CT (ti, rj))

(2) CTij = RTj+ETij

where CTij is Completion Time of task i on resource j, ETij is expected execution time of job i on resource j and RTj is the ready time or availability time of resource j; the time when machine rj complete execution of all the prior assigned tasks.

The flow time (Fi) is also referred to as the cycle time. It is the amount of time job ti spends in the job shop. It is the time interval between the release time rei (The time at which the job is released to the job shop.) and the completion time Ci of job ti:

(3) Fi = Ci - rei

Tardiness: (Ti) – The tardiness Ti of a job ti is the non-negative amount of time by which the completion time exceeds the due date di,. The differences between the completion time and due date for each job.

(4) Ti = max [0, (Ci - di)]

Resource Utilization for a particular problem is calculated using the formula,

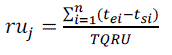where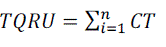

CT = Completion time of task

ruj= Resource utilization of a resource j

tei = End time of task i

tsi = Start time of task i

TQRU = Total quantity of resource used

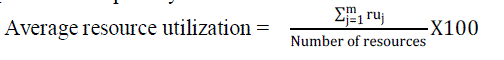GRID SCHEDULING ALGORITHMS

Grid Scheduling algorithms are majorly classified as Batch mode or Offline mode and Immediate mode or Online mode. In Batch mode, tasks are grouped together in Meta task (MT) and then the batch is scheduled in some predefined times called mapping events whereas in Immediate mode, task is mapped as soon as it arrived into the system. Min- Min, Max-Min algorithms are examples of Batch mode mapping whereas Minimum Execution Time (MET) and Minimum Completion Time (MCT) are examples of Immediate mode mapping.

A. Min-Min Scheduling Algorithm

The Min-Min Algorithm has two phases for task scheduling. In the first phase, it first finds the set of minimum completion time for all the tasks for the given resource. The second phase involves the selection of the minimum value from the minimum task set created by the first phase and assignment of the minimum selected task to the expected resource. The steps are repeated till all the tasks are mapped to the resources. One of limitation of Min-Min scheduling algorithm is load imbalance. The time complexity of this algorithm is O(RT2) time.

B. Max-Min Scheduling Algorithm

The Max-Min Algorithm is similar to the Min-Min algorithm. It also has two phases for task scheduling. In the first phase, it first finds the set of minimum completion time for all the tasks for the given resources. The second phase involves the selection of the maximum completion time value from the minimum task set calculated by the first phase for the given resource. The steps are repeated till all the tasks are mapped to the resources. The complexity of this algorithm is O(RT2) time.

C. Minimum Execution Time

This algorithm finds the task which has minimum execution time and assigns the task to the resource based on first come first served basis. One of the main drawbacks of this algorithm is load imbalance. It does not consider the availability of the resource and its load. It takes O(R) time to map a given job to an expected machine.

D. Minimum Completion Time

This algorithm finds the machine which has Minimum Completion Time for the particular task. It assigns the task to resources based on completion time. Completion time is calculated by adding the execution and the ready time of the resource. It takes O(R) time to map a given job to an expected resource.

RESULTS AND DISCUSSION

To analyze the four scheduling algorithms, Let us consider the problem having two resources R1 and R2 and the task group Ti consists of five tasks T1, T2, T3, T4 and T5. Table 1 gives the execution time and due time of the task. Using algorithms Min-Min, Max-Min, MET, MCT for the above given matrix, makespan, flowtime and tardiness of the jobs are calculated. Table 2 gives the calculated values of respective algorithms.

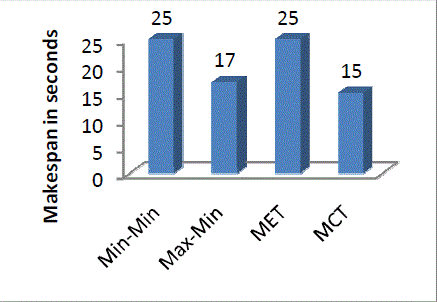
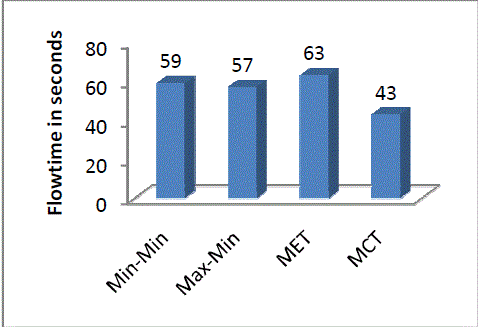
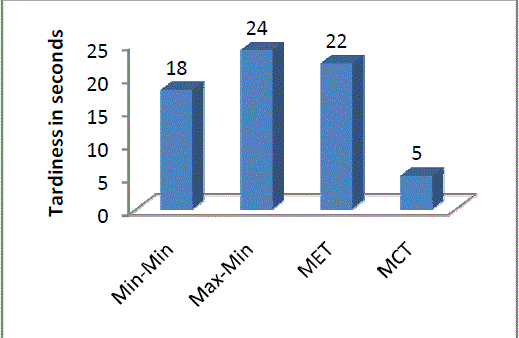
Figure 1, 2 and 3 shows the performance analysis of Min-Min, Max-Min, MET and MCT on the basis of Makespan, Flowtime and Tardiness respectively.

Minimum Completion Time minimizes the makespan compared to Minimum Execution Time Algorithm. Min-Min algorithm performs better in the case if there are large number of heavy tasks and few lighter tasks. Also, Max-Min performs better in the case if there are few heavy tasks and more light tasks.

Max-Min algorithm works better comparatively for the objectives makespan and flowtime, but the tardiness objectives gets maximized.

CONCLUSION

For achieving high throughput computing in grid heterogeneous environment, we need an efficient grid scheduling algorithm which finds optimal resource for the job user submits to the grid. In this paper four such conventional scheduling algorithms studied. This paper tried to identify their performance. This study is concentrated only on makespan, flowtime and tardiness. Many issues remain open. We did not consider deadline of each task, cost of execution on each resource, cost of communication and many other cases that can be a topic of research. Finally, we can hybrid these algorithms with new scheduling heuristic in an actual environment for practical evaluation.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2	Figure 3	Figure 4

References

Foster and Kesselman.C, “The Grid 2: Blueprint for a New Computing Infrastructure”, Morgan Kaufmann, USA, 2003.

HesamIzakian, Ajith Abraham, VáclavSnášel, “Comparison of Heuristics for Scheduling Independent Tasks on Heterogeneous DistributedEnvironments”, vol. 1, pp.8-12, 2009 International Joint Conference on Computational Sciences and Optimization, 2009.

T. D. Braun, H. J. Siegel, N. Beck, L. L. Boloni, M. Maheswaran, A. I. Reuther, J. P. Robertson, M. D. Theys, B. Yao, D. Hensgen, and R. F.Freund, "A comparison of eleven static heuristics for mapping a class of independent tasks onto heterogeneous distributed computing systems,"Journal of Parallel ad Distributed Computing, vol. 61, issue 6, pp. 810-837, Jun. 2001.

Thilagavathi, D., and Antony SelvadossThanamani. “A Survey on Dynamic Job Scheduling in Grid Environment Based on Heuristic Algorithms”, International Journal of Computer Trends and Technology (IJCTT), Vol.3, Issue 4, pp.531-536, 2012.

Ajith Abraham, Hongbo Liu, Weishi Zhang and Tae-Gyu Chang, "Scheduling jobs on computational grids using fuzzy Particle SwarmAlgorithm", KES2006 10th International Conference on Knowledge-Based & Intelligent Information &Engineering Systems, Bournemouth International Conference Centre, pp.500-507, October 2006.

M. Maheswaran, S. Ali, H. J. Siegel, D. Hensgen, and R. F. Freund, "Dynamic Matching and Scheduling of a Class of Independent Tasks ontoHeterogeneous Computing Systems, The 8th Heterogeneous Computing Workshop , pp. 30-44, Apr. 2001.

R. S. Chang, J. S. Chang, and P. S. Lin, “An ant algorithm for balanced job scheduling in grids”, Future Generation Computer Systems, Vol.25, pp.20-27, January 2009.

SaeedParsa, Reza Entezari-Maleki, RASA: A New Grid Task Scheduling Algorithm International Journal of Digital Content Technology andits Applications Volume 3, Number 4, December 2009.

G. Attiya and Y. Hamam. “Task allocation for maximizing reliability of distributed systems: A simulated annealing approach”, Journal ofParallel and Distributed Computing, 66, 2006, pp.1259 – 1266.

Y. Gao, H. Rong, and J. Z. Huang, “Adaptive grid job scheduling with genetic algorithms”, Future Generation Computer Systems, vol.21,pp.151-161, January 2005.

Thilagavathi, D., and Antony SelvadossThanamani. “Scheduling in High Performance Computing Environment using Firefly Algorithm andIntelligent Water Drop Algorithm.” International Journal of Engineering Trends and Technology (IJETT) – Vol.14, No.1, August 2014.

Mohd KamirYusof and MuhamadAzaharStapa, Achieving of Tabu Search Algorithm for Scheduling Technique in Grid Computing UsingGridSim Simulation Tool: Multiple Jobs on Limited Resource, International Journal of Grid and Distributed Computing Vol. 3, No. 4,December 2010.

Thilagavathi, D., and Antony SelvadossThanamani. “An Impression on Performance Metrics for Scheduling Problem in Grid Computing Environment.” International Journal of Research in Computer Applications and Robotics ISSN 2320-7345. Vol.2, Issue 8, pp.40-45, August2014.