International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Enhance Privacy Preserving In Location Based Service

Karthik R1, Anguraj S2
  1. M.Tech, Dept of IT, K.S.R. College of Engineering, Tamilnadu, India
  2. Assistant Professor, Dept of IT, K.S.R. College of Engineering, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Location Based Services (LBSs) have recently attracted much attention due to the advancementof GPS facilitates. In LBS, the private and confidential information of user may disclose to others since LBS need a user’s location. To protect the privacy of users, many cloaking algorithms have been proposed to hide user’s actual location. Here to improve the cloaking algorithm performance and location privacy.A fundamental approach to perform the class of k- Nearest Neighbor (k-NN) queries, the core class of queries used in many of the location-based services, without revealing the origin of the query in order to preserve the privacy of this information. The idea behind our approach is to utilize oneway transformations to map the space of all static and dynamic objects to another space and resolve the query blindly in the transformed space. However, in order to become a viable approach, the transformation used should be able to resolve k-NN queries in the transformed space accurately and more importantly prevent malicious use of transformed data by untrusted entities. Traditional encryption based techniques incur expensive O(n) computation cost (where n is the total number of points in space) and possibly logarithmic communication cost for resolving a K-NN[1] query. This is because such approaches treat points as vectors in space and do not exploit their spatial properties. In contrast, we use Hilbert curves as efficient one-way transformations and design algorithms to evaluate a K-NN query in the Hilbert transformed space. Consequently, we reduce the complexity of computing a K-NN query to and transferring the results to the client in O(K), respectively, where N, the Hilbert curve degree, is a small constant. Our results show that we very closely approximate the result set generated from performing KNN queries in the original space while enforcing our new location privacy metrics termed u-anonymity and a-anonymity, which are stronger and more generalized privacy measures than the commonly used K-anonymity and cloaked region size measures. AS a result, the security level of the proposed protocol is close to perfect secrecy without the aid of a trusted third party and simulation results show that the k- NN query accuracy rate of the proposed protocol is higher than 92% even when is large.

INTRODUCTION
A Location services can be defined as services that integrate a mobile device's location or position with other information so as to provide added value to a user. Location services have a long tradition. Since the 1970s, the U.S. Department of Defense has been operating the global positioning system (GPS), a satellite infrastructure serving the positioning of people and objects. Initially, GPS was conceived for military purposes, but the U.S. government decided in the 1980s to make the system's positioning data freely available to other industries worldwide. Since then, many industries have taken up the opportunity to access position data through GPS and now use it to enhance their products and services. For example, the automotive industry has been integrating navigation systems into cars for some time.
In order to resolve the problem, a privacy-preserving LBS is needed. For building a privacy preserving LBS, there are two major challenges: security and accuracy (in k-NN search). There are two major types of research works dealing with the prescribed challenges in the k-NN search of LBS which can be classified into 3-tier and 2-tier LBS architectures. The 3-tier architecture hides user’s location with the aid of a trusted third party (TTP) . There are some drawbacks when we rely the privacy-preserving LBS upon a TTP. First, in these approaches, a TTP is a must for hiding the location of user.
The TTP[2] knows too much sensitive information about the user and becomes a single point to be attacked. Second, the anonymized status or space transformed status of a user is breakable by applying the Background now ledge Attack or the Correlation Attack. Let’s take the cloaking technique as an example to illustrate the situation of being attacks. In a cloaking technique, the querying user is anonymized in the cloak region with the security level of k-anonymity[11], which means that no one can distinguish the querying user from other users in the cloak region. But cloaking technique is breakable by the Background Knowledge Attack. For example, if a female user Alice is querying for the nearest women hair salon and the other users in the cloak region are all happened to be male.
Then, server can identify the query is issued from Alice with high probability. Moreover, the cloaking techniques is also vulnerable to Correlation Attack. For example, server can narrow down the size of cloak region by analyzing the history or trajectory of user’s continuous queries, like “informing me the nearest rest stop coming up along the highway every 5 minutes in the next 30 minutes.” Another type of research works, the 2-tier architecture, utilizes Private- Information- Retrieval (PIR)[9][10] technique to hide the user’s location without the TTP. The PIR-based technique can resist Background Attack and Correlation Attack. In the most representative research work , the accuracy of k-NN search is near to 100% when , however, it will drop when increases. Therefore, on the basis of connected space-filling curves and homomorphic cryptosystems, an effective secure k-NN search protocol, Distance Based Private Circular Query Protocol (DBPCQP), is proposed to deal with the afforested two challenges.
In DBPCQP, the Moore’s version of Hilbert curve (or Moore curve in short) is selected as the mapping tool to transform POIs in 2-D space into 1-D space, and the LBS query is resolved in the 1-D transformed space with the proposed secret circular shift scheme[1]. The time-consuming space transformation effort is paid only in the initialization phase for building LBS. The resultant 2-D to 1-D space transformation can be repeatedly reused in the following queries. There are two benefits for applying the space transformation to POIs. First, the query in the transformed space is easier and faster to be carried out than the calculation of Euclidean distances between all POIs and the query location.

RELATED WORKS
A. Space-Filling Curves
Intuitively, a continuous curve in 2 or 3 (or higher) dimensions can be thought of as the path of a continuously moving point. To eliminate the inherent vagueness of this notion Jordan in 1887 introduced the following rigorous definition, which has since been adopted as the precise description of the notion of a continuous curve :A curve (with endpoints) is a continuous function whose domain is the unit interval [01].
In the most general form, the range of such a function may lie in an arbitrary topological space, but in the most commonly studied cases, the range will lie in a Euclidean space such as the 2-dimensional plane (a planar curve) or the 3- dimensional space (space curve)[1].Sometimes, the curve is identified with the range or image of the function (the set of all possible values of the function), instead of the function itself. It is also possible to define curves without endpoints to be a continuous function on the real line (or on the open unit interval (0,??1)).Space-filling curves represent a class of curves which can traverse through all cells in a 2-D space, or more generally, a multidimensional hypercube, without crossing themselves.
B. Homomorphic Cryptosystem
Homomorphic encryption[12] is a form of encryption which allows specific types of computations to be carried out on ciphertext and obtain an encrypted result which decrypted matches the result of operations performed on the plaintext. For instance, one person could add two encrypted numbers and then another person could decrypt the result, without either of them being able to find the value of the individual numbers.
A homomorphic cryptosystem is indispensable. Traditionally, there will be a TTP playing an important role to hide the user’s location in a location-based service. Without a TTP in our protocol, we can take the advantage of homomorphic cryptosystem to prevent user’s location information leak by conducting the service in homomorphic encryption domain on the LBS-server side. The property of a homomorphic cryptosystem is that some specifically algebraic operations on plaintext can be equivalently achieved in the encryption domain by other algebraic operations performed on the cipher text.
The product of two ciphertexts will decrypt to the sum of their corresponding plaintexts,
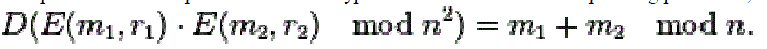image
The product of a ciphertext with a plaintext raising g will decrypt to the sum of the corresponding plaintexts,
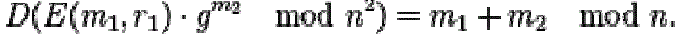image
An encrypted plaintext raised to the power of another plaintext will decrypt to the product of the two plaintexts,
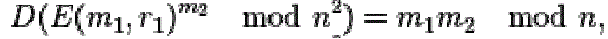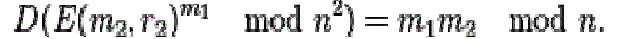image
image
More generally, an encrypted plaintext raised to a constant k will decrypt to the product of the plaintext and the constant,
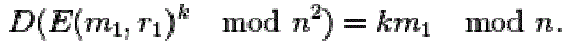image
C.Distance based private circular query protocol (DBPCQP)
For accomplishing privacy preserving LBS, in effective and efficient secure k-NN search scheme, called Distance Based Private Circular Query Protocol (PCQP), is proposed. DBPCQPnot only can improve the accuracy of k-NN search, but alsoprotect the query privacy from disclosure. More important, TTP is not required in DBPCQP.
Overview of DBPCQP
step-1: Server constructs a Moore curve and generates H-indexes for all registered POIs on the target map.
step-2: Server publicly announces the lookup-table and Moore curve’s setting parameters to the registered.
step-3: User exchange his/her public and private key pairs of the Paillier cryptosystem and sends the public-key to server.
step-4: User issues a k-NN query to server.
(a)User chooses an -offset circular shift permutation matrix, where denotes the number of POIs in H-table and the k-th element of the first row of is the only nonzero element in that row.
(b) User adds a number to the H-index of his/her current location to generate a shifted-H-index.
(c) User sends the shifted-H-index and the encrypted first row of by the public-key selected in step-3, denoted as , to server and issues a k-NN query.
step-5: Server performs a secret circular shift, which is de-fined by , on the POI-info column of H-table based on the Additive and Multiplicative homomorphism’s of Paillier cryptosystem with user’s public key. Server, then, conducts a k-NN search upon the circularly shifted H-table, and returns the encrypted search results back to user.
step-6: User uses his/her private key (selected in step-3) to decrypt the received results and finds the required k- NN solutions. Since H-index of the querying user and the POI-info column of H-table have respectively been added by (in step-4) and secretly circularly shifted by (in step-5), where , the secret k-NN search results done in the shifted H-table will be the same as that of the original k-NN search results done in their plaintext version.

i.k-nearest neighbors algorithm
In pattern recognition, the k-nearest neighbors algorithm (k-NN)[1] is a non-parametric method for classification and regression,[1] that predicts objects' "values" or class memberships based on the k closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until classification. The k-nearest neighbor algorithm is amongst the simplest of all machine learning algorithms: an object is classified by a majority vote of its neighbors, with the object being assigned to the class most common amongst its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of that single nearest neighbor.
The same method can be used for regression, by simply assigning the property value for the object to be the average of the values of its k nearest neighbors. It can be useful to weight the contributions of the neighbors, so that the nearer neighbors contribute more to the average than the more distant ones. (A common weighting scheme is to give each neighbor a weight of 1/d, where d is the distance to the neighbor. This scheme is a generalization of linear interpolation.) The neighbors are taken from a set of objects for which the correct classification (or, in the case of regression, the value of the property) is known. This can be thought of as the training set for the algorithm, though no explicit training step is required. The k-nearest neighbor algorithm is sensitive to the local structure of the data.
Nearest neighbor rules in effect implicitly compute the decision boundary. It is also possible to compute the decision boundary explicitly, and to do so efficiently, so that the computational complexity is a function of the boundary complexity.
ii.H-Index versus H-Value:
Onecanfind that the starting and the ending cells do not neighbor to each other. In this case, if the query position is near to the starting or ending cell of the curve, then the searching directions will be reduced from two to one, which is opposite to the starting or ending cell. Besides, one can also find that those H-value DB are only used to string all the POIs together in a locality-preserving order and behave as a tool for addressing all POIs in DB. As long as those H-values retain their numerical order, altering those H-values won’t affect the result of query because only the order of H-values is of concern in retrieving k-NN search results.
iii.Secret Circular Shift in H-Table:
The characteristics of Moore curve[], the POIs stored in H-table’s first and last rows are very close to each other, geographically. That is, despite whatever the H-index distance between the first and the last row would be, the two POIs neighbor to each other in the 2-D space, the first and the last rows of H-table could be thought of as linking together just like an edge had been added to connected the two ending points of the corresponding Moore curve.
iv.Paillier Cryptosystem:
The Pailliercryptosystem[13], is a probabilistic asymmetric algorithm for public key cryptography. The problem of computing n-th residueclasses is believed to be computationally difficult. The decisional composite residuosity assumption is the intractability hypothesis upon which this cryptosystem is based.
The scheme is an additive homomorphic cryptosystem; this means that, given only the public-key and the encryption m1of and m2, one can compute the encryption of m1+m2.
D.Distance Based Cross-Like k-NN Search Algorithm
This method is arrange by the K-NN[1][5][7] result is distance based. There are four border-center cells of a given adaptive search window, and the one with the farthest H-index[3] value from that of the center cell should have the highest priority to be searched first, where the four associated H-indexes can be calculated by user according to Moore curve’s[2][4] setting parameters and the lookup-table got from LBS website browsing.
In other words, for accomplishing a k-NN search, user is-suing at most 5-NN queries in this cross-like search algorithm at step-4 in DBPCQP, the corresponding complexity on user side would be, which is much less than that of the connected-path based k-NN search algorithm[8]. Moreover, the size of the server returned resultant set varies from to depending on the number of additional queries made by user. We will con-duct a series of experiments on a real world dataset in to verify the performance of the proposed cross-like search algorithm and will show that two instead of four additional queries are sufficient to achieve reasonable high accuracy rate in most cases.

CONCLUSION
The first phase, a Distance BasedPrivate Circular Query Protocol with Distance Based cross like search mechanism is proposed to simultaneously accomplish the location-based k-NN query and the location privacy preservation, in a novel way. To the best of our knowledge, this is the first work to apply Moore curves to location-based query problem in the literature. The security level of the proposed protocol is near to perfect secrecy without TTP and the accuracy rate is stably above 92% regardless of the variation of k. The proposed circular structure seamlessly integrates the robustness of specific public-key cryptosystems and the clustering property of space-filling curves. The proposed framework not only can address the challenges of privacy preserving LBS, but also inspire the research of secret computation with desired property to achieve privacy preserving information processing in the cloud computing era. The design of the proposed system is prepared to solve the problems in the existing system. Module level development procedures are also finalized in this paper.

References