International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Enhanced Order Crossover for Permutation Problems

Girdhar Gopal1, Rakesh Kumar2, Ishan Jawa3 and Naveen Kumar1
  1. Research Scholar, Dept. of Comp. Sci. & Applications, Kurukshetra University, Kurukshetra, Haryana, India
  2. Professor, Dept. of Comp. Sci. & Applications, Kurukshetra University, Kurukshetra, Haryana, India
  3. Assistant Professor, Dept. of Comp. Sci. & Applications, Kurukshetra University, Kurukshetra, Haryana, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper proposes a modified Order crossover operator for genetic algorithm that generates high quality solutions to the Traveling Salesman Problem (TSP) effectively. As the main time consuming process of crossover operator and schemata preserving process in crossover is the hole filling done in Order Crossover operator, so if the swath size is not to be too long and also depending on the problem size then it might be proven to find near optimum solutions in effective and efficient manner. The Modified Order Crossover operator constructs an offspring from a pair of parents using the existing Order Crossover operator with the enhancement on swath length (the size of a chromosome which is between two crossover sites). The efficiency of the Modified Order Crossover is compared as against some of the existing crossover operators; namely, Partially Mapped Crossover (PMX), Order Crossover (OX) & Cyclic Crossover (CX) for some benchmark TSPLIB instances. Experimental results suggest that the new crossover operator enabled improved results compared to the PMX, OX and CX for the five Travelling salesman problems tested

Keywords
Crossover Operator, Genetic algorithm, NP-complete, Order Crossover, Traveling salesman problem.

INTRODUCTION
The Traveling Salesman problem (TSP) is one of the benchmark and old problems in Computer Science and Operations Research. It can be stated as: A network with „n‟ nodes (or cities), with 1 node as main node and a travel cost (or distance, or travel time etc.,) matrix C= [Cij] of order n associated with ordered node pairs (i, j) is given. The problem is to find a least cost Hamiltonian cycle. On the basis of the structure of the cost matrix, the TSPs are classified into two groups – symmetric and asymmetric. The TSP is symmetric if Cij = Cji, ∀i,j and asymmetric otherwise. For an n-city asymmetric TSP, there are (n −1)! possible solutions for all n > 2, one or more of which gives the minimum cost. For an n-city symmetric TSP, there are (n −1)! / 2 possible solutions for all n > 2 along with their reverse cyclic permutations having the same total cost. In either case the number of solutions becomes extremely large for even moderately large n so that an exhaustive search is impracticable. There are mainly three reasons why TSP has been attracted the attention of many researcher‟s and remains an active research area. First, a large number of real-world problems can be modeled by TSP. Second, it was proved to be NP-Complete problem [1]. Third, NP-Complete problems are intractable in the sense that no one has found any really efficient way of solving them for large problem size. Also, NP-complete problems are known to be more or less equivalent to each other; if one knew how to solve one of them one could solve all of them. The TSP finds application in a variety of situations such as automatic drilling of printed circuit boards and threading of scan cells in a testable VLSI circuit [2], X-ray crystallography [3], etc. The methods that provide the exact optimal solution to the problem are called exact methods. An implicit way of solving the TSP is simply to list all the feasible solutions, evaluate their objective function values and pick out the best. However it is obvious that this “exhaustive search” is grossly inefficient and impracticable because of vast number of possible solutions to the TSP even for problem of moderate size. Since practical applications require solving larger problems, hence emphasis has shifted from the aim of finding exactly optimal solutions to TSP, to the aim of getting, heuristically, „good solutions‟ in reasonable time and „establishing the degree of goodness‟. Genetic algorithm (GA) is one of the best heuristic algorithms that have been used widely to solve the TSP instances. In this paper, A Modified Order Crossover operator is proposed and accordingly a genetic algorithm based on Modified Order Crossover is developed for solving the TSP. This paper is organized as follows: Section 2 describes a genetic algorithm Methodology. Section 3 describes related work on the problem. Section 4 describes proposed genetic algorithm based on Modified Order Crossover operator. Section 5 describes computational experiments for Modified Order Crossover and some of the existing crossover operators. Finally, Section 6 presents comments and concluding remarks.

GENETIC ALGORITHM
Genetic algorithms (GAs) are based essentially on mimicking the survival of the fittest among the species generated by random changes in the gene-structure of the chromosomes in the evolutionary biology [4]. In order to solve any real life problem by GA, two main requirements are to be satisfied: (a) a string can represent a solution of the solution space, and (b) an objective function and hence a fitness function which measures the goodness of a solution can be constructed / defined.
A simple GA works by randomly generating an initial population of strings, which is referred as gene pool and then applying operators to create new, and hopefully, better populations as successive generations. The first operator is selection where strings are copied to the next generation with some probability based on their objective function value. The second operator is crossover where randomly selected pairs of strings are mated, creating new strings. The third operator, mutation, is the occasional random alteration of the value at a string position. The crossover operator is the most powerful process in the GA search. Mutation diversifies the search space and protects from loss of genetic material that can be caused by reproduction and crossover. So, the probability of applying mutation is set very low, whereas the probability of crossover is set very high.
The search of the solution space is done by creating new chromosomes from old ones. The most important search process is crossover. Firstly, a pair of parents is randomly selected from the mating pool [5]. Secondly, a point, called crossover site, along their common length is randomly selected, and the information after the crossover site of the two parent strings are swapped, thus creating two new children. Of course, this basic crossover method is not applicable for the TSP as it may repeat some of the cities lying on different sides of parents and may ignore some of the cities also, so new crossover operators are designed for TSP problems.

RELATED WORK
Since the crossover operator plays a vital role in GA, so many crossover operators have been proposed for the TSP. Goldberg and Lingle [6] defined an operator called PMX (partially mapped crossover). This operator first randomly selects two cut points on both parents. In order to create an offspring, the substring between the two cut points in the first parent replaces the corresponding substring in the second parent. Then, the inverse replacement is applied outside of the cut points, in order to eliminate duplicates and recover all cities. Consider two possible codings of a tour of eight cities, A1 and A2.
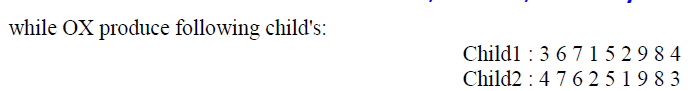Image
Image
Another crossover operator, named CX (cycle crossover) operator was proposed by Oliver et al. [8], where offspring are built in such a way that each node (and its position) comes from one of the parents. Whitley et al. [9] proposed edge recombination crossover (ERX) operator that uses an „edge map‟ to construct an offspring that inherits as much information as possible from the parent structures. This edge map stores all the connections from the two parents that lead into and out of a node. A crossover operator based on the conventional N-point crossover operator, named as generalized N-point crossover (GNX), was proposed by Radcliffe and Surry [10]. Poona and Carter [11] developed a tie break crossover (TBX), which was then modified by Choi et al. [12] by combining PMX and TBX operators. Moon et al. [13] proposed a new crossover operator named Moon Crossover (MX), which mimics the changes of the moon such as waxing moon → half moon → gibbous → full moon. As reported, performance of MX operator and OX operator is almost same, but OX never reached an optimal solution for all trials.

PROPOSED GENETIC ALGORITHM
A. Genetic coding
To apply a GA for any optimization problem, one has to think a way for encoding solutions as feasible chromosomes so that the crossovers of feasible chromosomes result in feasible chromosomes. The techniques for encoding solutions vary by problem and, involve a certain amount of art. For the TSP, a solution is typically represented by chromosome of length as the number of nodes in the problem.
Each gene of a chromosome takes a label of node such that no node can appear twice in the same chromosome. There are mainly two representation methods for representing tour of the TSP: adjacency representation and path representation. Path representation for a tour is considered in this model which simply lists the label of nodes. For example, let {1, 2, 3, 4, 5} be the labels of nodes in a 5 node instance, then a tour {1→ 3→4→ 2→ 5 →1} may be represented as (1, 3, 4, 2, 5).
B. Fitness function
The GA is usually used for optimization problems and TSP is an optimization problem; a function f(x) which calculates cost of the tour represented by the chromosome „x‟ is considered as fitness function for that chromosome.
C. Selection operator
In selection process, chromosomes are copied into next generation mating pool with a probability associated with their fitness value. By assigning to next generation a higher portion of the highly fit chromosomes, selection mimics the Darwinian survival-of-the-fittest in the natural world.
In natural population, fitness is determined by a creature‟s ability to survive predators, pestilence, and other obstacles to adulthood and subsequent reproduction. In this phase no new chromosome is produced. The commonly used reproduction operator is the proportionate reproduction operator, where a string is selected for the mating pool with a probability proportional to its fitness value. Roulette Wheel selection method is used as selection operator in this study.
D. Modified OX crossover operator (MOX)
The modified OX crossover (MOX) operator constructs an offspring from a pair of parents using the existing OX operator with the enhancement on swath length. As the main time consuming process of crossover operator and schemata preserving process in crossover is the hole filling done in OX operator, so if the swath size is not to be too long and also depending on the problem size then it might be proven to find near optimum solutions in effective and efficient manner. In crossover operator the length of a substring is chosen randomly. Thus on an average, the length is equal to n/2. A big swath will lead to a marked increase in the computational time as more work to do, which can be reduced if the length of the substring for performing crossover can be fixed to a small value. An attempt is made in this article for determining an appropriate value of the length of a substring for performing crossover. A number of experiments are done to find such a value in this research and it is found that a substring length „l‟ for MPMX provides good results for TSP if l = max{3, β}, where n/9 ≤ β ≤ n/7 (where n is the total number of cities). Obviously one can tune the constants according to the problem.
Holland's schema theorem is widely taken to be the foundation for explanations of the power of genetic algorithms. It says that short defining length, low-order schemata with above-average fitness increase exponentially in successive generations. The order of a schema o(H) is defined as the number of fixed positions in the template, while the defining length d(H) is the distance between the first and last specific positions. Goldberg and Lingle introduced the partially mapped crossover (PMX) operator and the notion of ordering schemata, or o-schemata. For o-schemata, the symbol „!‟ acts as a wild card match symbol. Thus the below template represents all permutations with one at third place, three at sixth place and seven at seventh place out of eight places. A „!‟ in chromosome below represent any of the remaining cities.
Image
The OX operator takes the swath elements from second parent and then fills the holes accordingly in the first child. As the swath size denotes the order of schemata and other holes denotes the wild card character in child. On an average the swath size is chosen randomly and is approximately n/2 which makes the schemata of high order and long defining length so an attempt is made to make the schemata short which fits the fundamental theorem of genetic algorithms.
Three more crossover operators – Partially Mapped Crossover (PMX), Order Crossover (OX) & Cyclic Crossover (CX) for producing offspring using the same pair of parents P1 and P2 are considered for comparison.
E. Mutation operator
The mutation operator randomly selects a position in the chromosome and changes the corresponding allele, thereby modifying information. The need for mutation comes from the fact that as the less fit members of successive generations are discarded; some aspects of genetic material could be lost forever. By performing occasional random changes in the chromosomes, GA ensure that new parts of the search space are reached, which selection and crossover alone couldn‟t fully guarantee. In doing so, mutation ensures that no important features are prematurely lost, thus maintaining the mating pool diversity. For the TSP, the classical mutation operator does not work. For this investigation, the reciprocal exchange mutation that selects two nodes randomly and swaps them has been considered.
F. Replacement
After performing crossover and mutation operation replacement method is used for selecting next generation population. The replacement of GA considers two kinds of chromosomes for the next generation: (1) parents in current population of size m, and (2) offspring that are generated by crossover of size m. The (μ,λ) replacement method that replace chromosomes in (1) by (2) completely is considered. In this case, all the μ parents in the present generation are replaced with next generation.
G. Control parameters
There are a lot of parameters that govern the GA search process. Some of them are:
(i) Population size: - It determines how many chromosomes and thereafter, how much genetic material is available for use during the search. If there is too little, the search has no chance to adequately cover the space. If there is too much, the GA wastes time evaluating chromosomes.
(ii) Crossover probability: - It specifies the probability of crossover occurring between two chromosomes.
(iii) Mutation probability: - It specifies the probability of doing mutation.
(iv) Termination criteria: - It specifies when to terminate the genetic search.

COMPUTATIONAL EXPERIMENTS
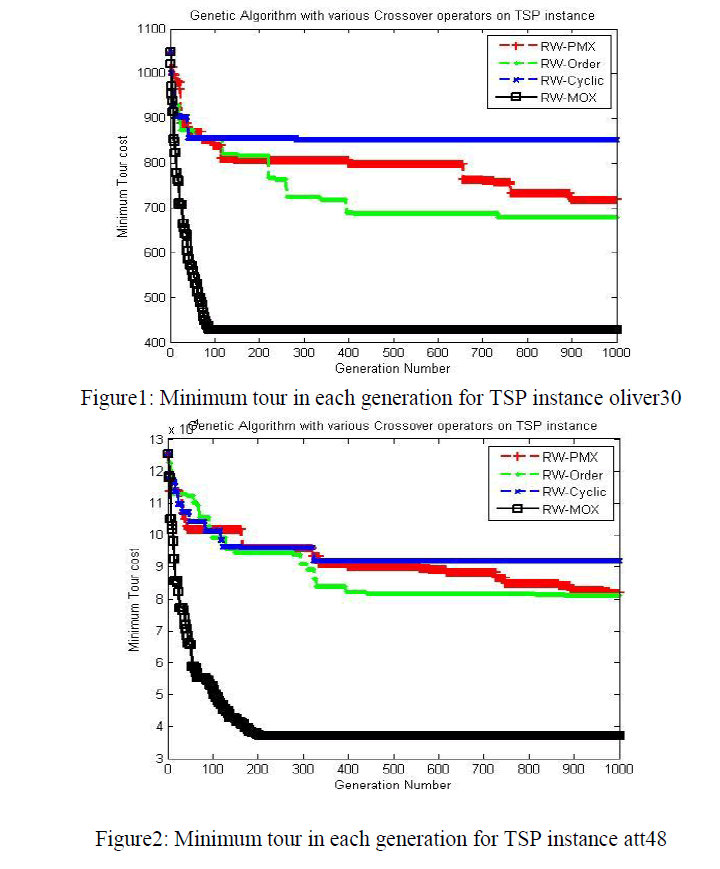
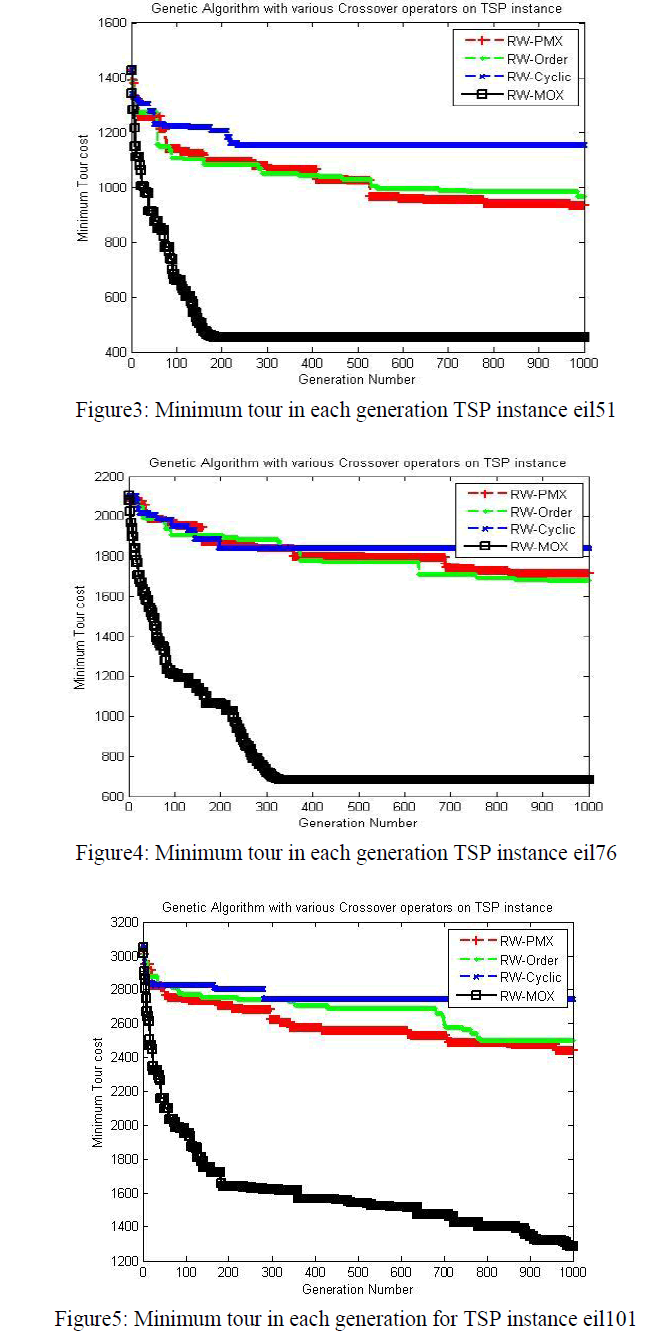
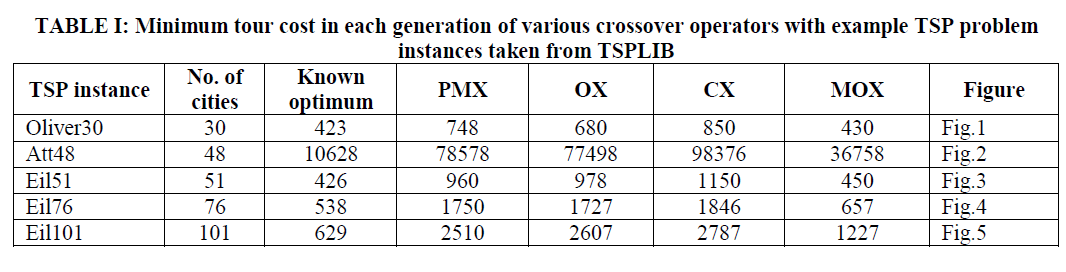
For comparing the efficiency of the different crossover operators in genetic algorithm using MOX, PMX, OX and CX have been encoded in MATLAB 2013b on a Pentium Core i5 personal computer with speed 2.1 GHz and 4 GB RAM under UBUNTU 12.04, and for many TSPLIB [14] instances. Initial population is generated randomly.
The following common parameters are selected for the algorithms: population size is 700, Population size is set to very high to obtain exact solution as was done by Whitley et al. [9] probability of crossover is .80 (i.e., 80%), probability of mutation is 0.01 (i.e., 1%), and maximum of 1,000 generations as the terminating condition. The experiments were performed 30 times for each instance. Several instances of TSP problem are taken from TSPLIB [14] for experiments and results are shown below in figures and tables:
The problem instances are coded with various crossover operators and time to run the algorithms is measured based on CPU seconds elapsed since the algorithm starts to the end output it produced. Based on these facts following results are popped on random runs of all instances.
Image
Image
Image

CONCLUSION
A modified OX crossover operator (MOX) for a genetic algorithm for the Traveling Salesman Problem (TSP) has been proposed. A comparative study among MOX, PMX, OX and CX for some benchmark TSPLIB instances has been provided. In terms of quality of the solution, for all the instances MOX found to be better in terms of solution quality and the overall time taken by the algorithm. Among all the operators, experimental results show that Modified OX crossover operator (MOX) is better than the PMX, OX and CX, in terms of quality of solutions as well as execution time.
Any local search technique is not used to improve the solution quality. So an incorporation of good local search technique to the algorithm may solve exactly more instances, which is under consideration.

References
  1. Papadimitriou C.H. and Steglitz K. (1997), “Combinatorial Optimization: Algorithms and Complexity”. Prentice Hall of India Private Limited, India.
  2. Ravikumar C.P. (1992) "Solving Large-scale Travelling Salesperson Problems on Parallel Machines”. Microprocessors and Microsystems 16(3), pp. 149-158.
  3. Bland R.G. and Shallcross D.F. (1989), "Large Travelling Salesman Problems arising form Experiments in X-ray Crystallography: A Preliminary Report on Computation". Operations Research Letters 8, pp. 125-128.
  4. Goldberg D.E. (1989), "Genetic Algorithms in Search, Optimization, and Machine Learning". Addison-Wesley, New York.
  5. Deb K. (1995) “Optimization For Engineering Design: Algorithms And Examples”. Prentice Hall Of India Pvt. Ltd., New Delhi, India.
  6. Goldberg D.E. and Lingle R. (1985), “Alleles, Loci and the Travelling Salesman Problem”. In J.J.Grefenstette (ed.) Proceedings of the 1st International Conference on Genetic Algorithms and Their Applications. Lawrence Erlbaum Associates, Hilladale, NJ.
  7. Davis L. (1985), “Job-shop Scheduling with Genetic Algorithms”. Proceedings of an International Conference on Genetic Algorithms and Their Applications, pp. 136-140, 1985.
  8. Oliver I.M., Smith D. J. and Holland J.R.C (1987), “A Study of Permutation Crossover Operators on the Travelling Salesman Problem”. In J.J. Grefenstette (ed.). Genetic Algorithms and Their Applications: Proceedings of the 2nd International Conference on Genetic Algorithms. Lawrence Erlbaum Associates, Hilladale, NJ, 1987.
  9. Whitley D., Starkweather T. and Shaner D. (1991), “The Traveling Salesman and Sequence Scheduling:Quality Solutions using Genetic Edge Recombination”. In L. Davis (Ed.) Handbook of Genetic Algorithms. Van Nostrand Reinhold, New York, pp. 350-372.
  10. Radcliffe N.J. and Surry P.D. (1995), “Formae and variance of fitness”. In D. Whitley and M. Vose (Eds.) Foundations of Genetic Algorithms 3. Morgan Kaufmann, San Mateo, CA, pp. 51-72.
  11. Poon P. and Carter J. (1995), “Genetic algorithm crossover operations for ordering applications”. Computers and Operations Research 22, pp. 135–47.
  12. Choi I., Kim S. and Kim H. (2003), "A genetic algorithm with a mixed region search for the asymmetric traveling salesman problem". Computers & Operations Research 30, pp. 773 – 786.
  13. Moon C., Kim J., Choi G. and Seo Y (2002), "An efficient genetic algorithm for the traveling salesman problem with precedence constraints". European Journal of Operational Research 140, pp. 606-617.
  14. TSPLIB, http://www.iwr.uni-heidelberg.de/iwr/comopt/software/TSPLIB95/