Feature subset selection using filtering with
Mutual information and Maximal information
coefficient

C.Gayathri

Feature subset selection using filtering with Mutual information and Maximal information coefficient

C.Gayathri

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Feature subset selection involves identifying a subset of the most useful features that produces compatible results as the original entire set of features. A feature selection algorithm may be evaluated from both the efficiency and effectiveness points of view. While the efficiency concerns the time required to find a subset of features, the effectiveness is related to the quality of the subset of features. Current existing algorithms for feature sub set selection works only based on conducting statistical test like Pearson test or symmetric uncertainty test to find the correlation between the features and apply threshold to filter redundant and irrelevant features. FAST algorithm uses symmetric uncertainty test for feature subset selection. In this work I extend the FAST algorithm by applying the Mutual information and maximal information coefficient to improve the efficiency and effectiveness of the feature subset selection.

INTRODUCTION

Feature selection is typically a search problem for finding an optimal or suboptimal subset of m features out of original M features. Feature selection is important in many pattern recognition problems for excluding irrelevant and redundant features. It allows reducing system complexity and processing time and often improves the recognition accuracy. With the aim of choosing a subset of good features with respect to the target concepts, feature subset selection is an effective way for reducing dimensionality, removing irrelevant data and redundant data, increasing learning accuracy, and improving result comprehensibility. Of the many feature subset selection algorithms, some can effectively eliminate irrelevant features but fail to handle redundant features, yet some of others can eliminate the irrelevant while taking care of the redundant features.A well known example is Relief [1] which weighs each feature according to its ability to discriminate instances under different targets based on distance-based criteria function. However, Relief is ineffective at removing redundant features as two predictive but highly correlated features are likely both to be highly weighted [2]. Relief-F [3] extends Relief, enabling this method to work with noisy and incomplete data sets and to deal with multi-class problems, but still cannot identify redundant features.

Many feature subset selection methods have been proposed and studied for machine learning applications. They can be divided into four broad categories: the Embedded, Wrapper, Filter, and Hybrid approaches.

METHODS FOR MACHINE LEARNING APPROACHES

A.Embedded Method:

The embedded methods incorporate feature selection as a part of the training process and are usually specific to given learning algorithms, and therefore may be more efficient than the other three categories. Traditional machine learning algorithms like decision trees or artificial neural networks are examples of embedded approaches.

B.Wrapper Method:

The wrapper methods use the predictive accuracy of a predetermined learning algorithm to determine the goodness of the selected subsets, the accuracy of the learning algorithms is usually high. However, the generality of the selected features is limited and the computational complexity is large.

C.Filter Method:

The filter methods are independent of learning algorithms, with good generality. Their computational complexity is low, but the accuracy of the learning algorithms is not guaranteed which leads to less result comprehensibility.

D.Hybrid Method:

The hybrid methods are a combination of filter and wrapper methods by using a filter method to reduce search space that will be considered by the subsequent wrapper. They mainly focus on combining filter and wrapper methods to achieve the best possible performance with a particular learning algorithm with similar time complexity of the filter methods.

FAST ALGORITHM

Fast Algorithm is a filter based mechanism to filter out the irrelevant and redundant features. Our solution involves using two correlation metrics for feature subset selection.

For irrelevant feature removal we use symmetric uncertainty. For identifying the redundant features & removing it we use clustering with mutual information and maximal information coefficient.

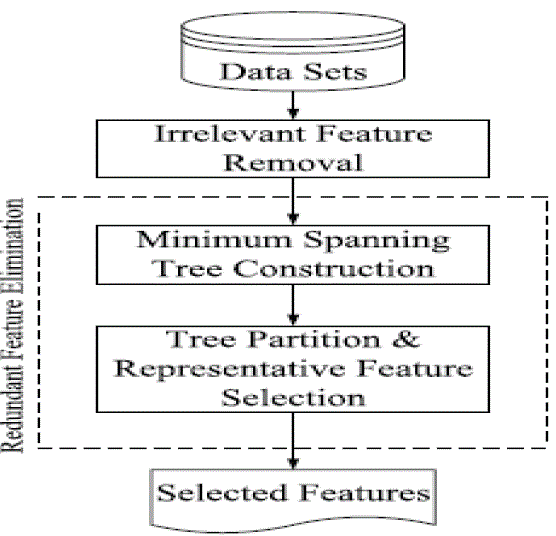A.Removing irrelevant Features

When the dataset with the features and the class is given, removal of irrelevant features is done. Between each features and the class, we calculate the symmetric uncertainty. The symmetric uncertainty is defined as follows

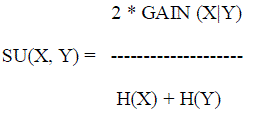Where

H(X) is the entropy of a discrete random variable X.GAIN (X|Y) = H(X) – H (X|Y)

H (X|Y) is the conditional entropy which quantifies the remaining entropy (i.e. uncertainty) of a random variable given that the value of another random variable is known.Between each feature to the class the SU (Fi, C) is calculated. The average of these values is taken.

B.Removing redundant Features

Once the irrelevant features are removed, we start to find the redundant features and remove those features. As a first step between each pair of features, we need to calculate the mutual information coefficient.

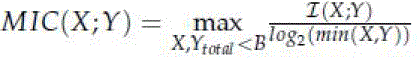Where I is naïve mutual information score given by

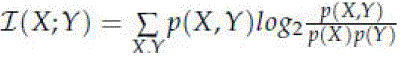-p(X, Y) is the joint distribution of X and Y.

MIC value between any two features is then normalized to value from 0 to 1. 1 indicates stronger correlation and 0 indicates no correlation. Once normalization is done, the proposed solution for redundancy removal works on it. Once features like this are selected, they have to undergo validity test.

Validity test is done by creating the clustering with the selected features in the step & checking the validity of class label. If the class label is same as the original

CONCLUSION

In this paper, I have detailed our solution for feature subset selection. Our mechanism effectively removes the irrelevant & redundant features from the feature set.

Our proposed solution is different from the FAST algorithm [9] in following ways.

1. FAST uses the Symmetric uncertainty measure for both redundancy & relevancy. But in our solution we have proposed a strong measure based mutual information coefficient for relevancy.

2. Our solution involves solving redundancy feature elimination in steps using iterations. Also with the solution of validity test for class label we are able to remove the redundant features effectively without any loss. But MST based solution used in FAST removes certain features are redundant even though there are not redundant data.

As the future work, I have planned to compare the performance of the proposed algorithm with that of the FAST algorithm on the 35 publicly available image, microarray, and text data from the four different aspects.

References

Kira K. and Rendell L.A., The feature selection problem: Traditional methods and a new algorithm, In Proceedings of Nineth NationalConference on Artificial Intelligence, pp 129-134, 1992.

Koller D. and Sahami M., Toward optimal feature selection, In Proceedings of International Conference on Machine Learning, pp 284-292, 1996.

Kononenko I., Estimating Attributes: Analysis and Extensions of RELIEF, In Proceedings of the 1994 European Conference on MachineLearning, pp 171-182, 1994.

Yu L. and Liu H., Feature selection for high-dimensional data: a fast correlation-based filter solution, in Proceedings of 20th InternationalConference on Machine Leaning, 20(2), pp 856-863, 2003.

Fleuret F., Fast binary feature selection with conditional mutual Information, Journal of Machine Learning Research, 5, pp 1531-1555, 2004.

Butterworth R., Piatetsky-Shapiro G. and Simovici D.A., On Feature Selection through Clustering, In Proceedings of the Fifth IEEEinternational Conference on Data Mining, pp 581-584, 2005.

Van Dijk G. and Van Hulle M.M., Speeding Up the Wrapper Feature Subset Selection in Regression by Mutual Information Relevanceand Redundancy Analysis, International Conference on Artificial Neural Networks, 2006

Krier C., Francois D., Rossi F. and Verleysen M., Feature clustering and mutual information for the selection of variables in spectral data, In Proc European Symposium on Artificial Neural Networks Advances in Computational Intelligence and Learning, pp 157-162, 2007.

A Fast Clustering-Based Feature Subset Selection Algorithm for High Dimensional Data - QinBao Song in "IEEE TRANSACTIONS ONKNOWLEDGE AND DATA ENGINEERING VOL:25 NO:1 YEAR 2013"