Keywords
|
| Discrete Fourier Transform, Orthogonal, Inner product, Fast Fourier Transform, Group, Algebra, Schwarz, Simplex method, Conformal map |
INTRODUCTION
|
| If mathematicians were asked the single most important discovery in all of mathematics, the Fourier series / transform should rightly rank as one of the most fundamental discoveries in mathematics (if not "the: most important mathematical discovery). It permeates all aspects of science and engineering (and even life) , from the most abstract environs of modern physics such as symmetry / quantum mechanics to applied areas such as imaging, holography, crystallography, areas in signal processing covering compression, multiplexing, modulation etc. Variants of the same are found in standards for audio and video signals such as JPEG , MPEG etc. So, improving the performance of the algorithms implementing the above transform assumes great importance. |
MATHEMATICAL FOUNDATIONS
|
The essence of the Fourier transform is the idea that a periodic function (with period 2*T for example) can be expanded as) 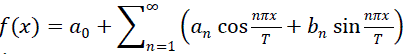 with with 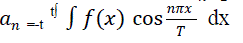 where the intervals of integration are from -t to t, using the orthogonality relationship between where the intervals of integration are from -t to t, using the orthogonality relationship between  and between cos and sine functions.. and between cos and sine functions.. |
| The Fourier series is one of the primary examples of orthogonal expansions/decompositions which has been generalized / extended to other orthogonal families such as Legendre, Chebyshev, Bessel etc generalizing the notion of orthogonality to abstract spaces such as Hilbert spaces etc where the notion of angle / dot product is generalized through the notion of "inner product" and associated "norm" and "metric". |
| One of the major applications of Fourier transform has been in transforming differential equations to algebraic equations thus enabling algorithmic implementations. |
| The topic of harmonic functions with applications and deep roots in complex analysis has its beginnings in Fourier Analysis. |
| A direct application of the above in physics is in the theory of Diffraction where the far field diffraction pattern in the Frauhnofer regime is the spatial Fourier transform of the unit cell. |
| Another direction of generalization has been through the notion of reciprocal space / phase space etc in quantum mechanics and modern physics where a joint time/space-frequency space is used for analysis. This leads to the "Heisenberg Uncertainty Principle". Ironically, Fourier series / orthogonal functions again provide a way out through the notion of self-dual functions (such as Solitons, Gaussians etc) that are invariant under the transform operator , i.e.they are their own transforms and through the possibility of realizing more precise / sharper bounds through the use of multiple , possibly overlapping but orthogonal waveforms. |
| The notion of periodicity is extended to more general symmetry groups as well as more generalized higher dimensional spaces in the theory of automorphic functions, modular forms, representation theory , harmonic groups etc where one seeks to quantify the symmetry operations to which an object is invariant (with possible links to quasicrystals, Penrose tilings etc). |
| A more direct connection is between the roots of unity and cyclic groups with the goal of establishing a correspondence between the former and extensions in the latter. |
| Another direction is in the direction of adaptive data driven basis functions extracted through algorithms such as Singular Value Decomposition etc |
| Out of the major properties of the Fourier transform, the links between modulation and convolution as transform pairs is key and which will be examined in the next section. |
DISCRETE FOURIER TRANSFORM ETC
|
| Polynomial multiplication can be looked at as a convolution, especially if the coefficients can be thought of as representing a vector. |
| Since multiplication/modulation (component wise) in the original time / space domain corresponds to convolution in the Fourier domain (and vice versa), we could simplify multiplication substantially by multiplying component wise , if the transform and the inverse can be computed quickly. |
| The real advantages become important when many such polynomials have to be multiplied together, for example in case of computations involving matrix of functions etc . |
| A really interesting possibility is that of inverting the above to factorize polynomials, i.e. , given a polynomial, we compute its transform and then factorize each of the components and then try to invert the transform. One problem is that the factors seem to get mixed up (which again seemed to be linked to the Fourier transform) But a hypothesis that would be interesting to investigate is that these could possibly correspond to symmetries possessed by the polynomial and / or possibly unique prime factors possibly ensuring reconstructability. |
| The other approach of course is to take into account the norm and height of the original polynomial and incorporate these in the factoring so that it becomes a constrained optimization problem |
| Yet another approach seems to be to try to create/maintain self similar distributions in the sense of the relative magnitude of the various coefficients. |
| One problem of course is that the coefficients could be complex , necessitating the use of group theory and connecting it to such discrete structures such as Gaussian primes etc. |
| Of course, an alternative approach is to expand it in terms of other family of orthogonal functions such as Legendre Polynomials etc |
| More details : |
Discrete Fourier Transform (DFT)
|
| •Evaluate a polynomial ) of degree-bound at the complex th ro ts of unity, 0, 1, 2. n-1. –assume that is a power of 2 |
| –assume ?? is given in coefficient form a;=(a;0,a;1…, a;n-1) |
 |
| The idea is to avoid cumbersome and messy interpolation formulae (Lagrange's interpolation formula) when moving from the point-value representation of the polynomial (where the multiplication can be done component wise) to the coefficient form in addition to the O(n2) complexity which also arises because of the complexity of evaluation[2] and [7] |
| The FFT etc use the symmetries related to scaling (usually 2) to reduce the complexity to O(nlog(n)). The next section seeks not only to improve on the above but also attempt to locate the singularities by exploiting larger / more general symmetry groups. |
GOING A STEP FURTHER , SCHWARZ PRINCIPLE AND APPLICATIONS
|
| The Schwarz reflection principle in Complex Analysis is an attempt to extend the function analytically (as an analytic function). One of the usual ways is through reflections across the real axis, i.e. F(z') = (F(z))' where ' denotes the conjugate operation. [1] |
| One way of extending the above is reflection across an arc of the circle (inversion). The other, of course is extension along the curve, in this case, the circular arc, i.e. analytic continuation of the function from one vertex of the n-sided regular polygon to another. |
| More specifically, if we denote the operator associated with moving from one point on the curve to another (for example, the rotation operator) by G (which would usually be a geometric symmetry group, when does the following hold : |
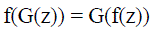 |
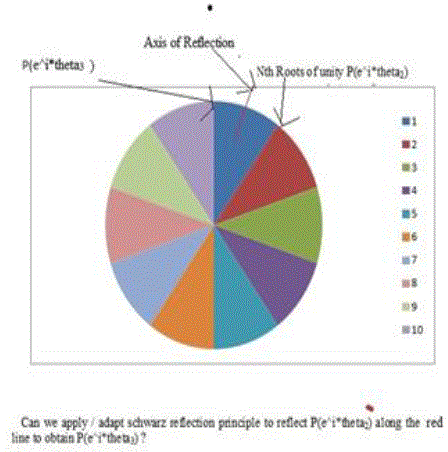
| That is the question that is being posed in the figure below which represents a unit circle with N nth (in this case 10) roots of unity corresponding to the sides of an n-gon. The idea is to analytically continue P(x) (where P = 1/W(x) with W(x) polynomial) from e^itheta2 across the red line to e^itheta3 |
| The answer to the above question seems to be a qualified affirmative in the sense, that one could analytically continue the function along the other nth roots of unity forming the vertices of a n-sided regular polygon (essentially rotating the red line to the real axis, performing the reflection (conjugation) and then reflecting back) "TILL" one reaches a singularity of the function (possibly, in a projective sense, since we are looking at evaluation of the function on the unit circle). This is linked to the idea / hypothesis that P(x) behaves like a Conformal Map. This is similar to the idea that the domain of definition of an analytic region is divided into domains / regions which are defined by singularities. In this case, conformality is important since it preserves inner products and angles and hence P(e^i*theta*x) = e^i*theta*P(x) since polynomials and their reciprocals are not only conformal but analytic / holomorphic and all analytic functions are conformal "except locally near singularities. Of course this conformality has to also take care of periodicity , (possibly through the logarthmic derivative function P'(x) / P(x) where P'(x) is the derivative of P(x) or by looking within one period or the fundamental domain or essentially looking at equivalence classes but since we are looking at reciprocals of polynomials, this should not be a problem) Another related perspective is the following : |
| If W(x) can be expanded in terms of an orthogonal family of Polynomials , (for example, Chebyshev which seems most apt) as : |
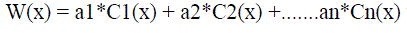 in the case of modulated materials etc with spatio-temporally varying properties) except in the case where both the vectors, functions are the same when the inner product becomes the norm..). Ci(x) stands for the ith Chebyshev polynomial in the case of modulated materials etc with spatio-temporally varying properties) except in the case where both the vectors, functions are the same when the inner product becomes the norm..). Ci(x) stands for the ith Chebyshev polynomial |
| If we look at the rotation operator in 2 dimensions as A and also look at W and C as operators and x as a 2 dimensional vector, then A(W(x) = a1*AC1(x) + a2*AC2(x) +.......an*ACn(x) which can be possibly cast in the form : a1*C(1+k)(x) + a2*C(2+k)(x) +......an*C(n+k)(x) where the additional term k in the argument possibly stands for the action of A (possibly relating to the action of A which would most possibly be a rotation of the form e^i*k and which has the effect of composition / multiplication of Chebyshev polynomials) |
| It would be really interesting if the unit circle is mapped to itself. |
| What is interesting is that any singularity in a particular arc/sector/region would destroy this conformality and invariance of the inner product and hence all one needs to do is to evaluate P(x) at the start and ending of each sector. If P(A(start)) <> P(end), we would know that there is a singularity and we can drill down further. |
| And since most nth degree polynomials would have the number of distinct zeros << n, this could help in speeding up evaluation of the function as also in factorization etc and since most functions could be closely approximated by polynomials of appropriate degree (Stone Weirstrass theorem etc), it would help in locating singularities/residues of functions (with applications to imaging, locating bottlenecks in flows with applications to fluid mechanics, power distribution, surgery etc). Once the direction of the singularity is located, one could use optimization techniques to reach the singularity. Another advantage is of course, the possibility of massively parallel evaluation at the different roots of unity. |
| The above has also relevance to the idea of detecting discontinuities in functions and adaptively smoothing them (as in the case of piecewise continuous curves) through localized but smooth functions such as the Tanh / Sigmoidal functions etc (links to Gibbs discontinuities in Fourier theory etc) |
| Also, since 1/f(x) type of inversions are typically related to Fourier transforms / reciprocal space, they could find applications in the theory of diffraction |
| The above may also be useful in the case of evaluation / asymptotic approximation of very complex functions such as the partition function (The famous "Circle Method') |
| An interesting point is that Chebyshev Polynomials are a class of functions help spread the error due to approximation / truncation most uniformly. |
| A related idea is the link between an infinite series and its associated limit integral (passing from Fourier series to transform) by evaluating the function at roots of unity related to incommensurate multiples of the arc-length (Links to Band gap in Materials etc) (Prob 19 ,Exercise section of Chapter 8 titled "Some special functions", Page 200 from [9]) |
| From a more fundamental viewpoint, the above has relevance to topics such as homotopy theory in Algebraic Topology. |
| One interesting link relates to the application of the above to optimization problems, especially relating to Karmarkar's interior point algorithm in Linear Programming (could possibly be adapted to nonlinear programming) where a vertex of a multidimensional polytype becomes the origin of a transformed coordinate system with the choice of next vertex reduced to a 2 step problem : determining the direction of steepest descent and determining the length of travel along this direction (essentially , determining the next vertex as the intersection of the gradient / direction of steepest descent with a lower dimensional projection of the polytype, especially if we look at hierarchically graded 2 dimensional subspaces of the multi-dimensional polytype which would enable the full application of the machinery of analytic functions. |
| At a higher level, one could look at homomorphism's (extensible to homeomorphisms ?) between algebras of operators and functions and the algebra associated with the underlying space / group / semigroup etc , in this case, that of complex numbers. Essentially, is G (or F) (a*b) = G(a)@G(b) where G (and F) denote operators, a and b denote functions or complex numbers respectively and * denotes the operation in the underlying space and @ denotes the operation in the space/algebra of operators (possible links to Gelfand theorem in Functional Analysis ?) [4] and [5] |
CONCLUSION
|
| Some interesting future possibilities relate to the possible applications of quantum / optical computing etc in implementing the Fourier transform. [8] talks about the possibility of applying Fourier methods to synthesis of mechanisms which act as function / path generators. [6] talks about /hints at about the possibility of extending these methods to navigation in abstract higher dimensional spaces including mathematical logic, information compression, molecular logical circuits, molecular synthesis etc in addition to the ones mentioned in [8]. |
Figures at a glance
|
 |
| Figure 1 |
|
References
|
- Lars Ahlfors , 'Complex Analysis'.
- Boaz Porat, 'A course in Digital Signal Processing'
- Gerald Kaiser , 'A friendly guide to wavelets '
- Robert Jewett, 'Spaces with an Abstract Convolution of Measures', Advances in Mathematics 18, 1-101 (1975).
- Tom.H. Koornwinder , 'Positive Convolution Structures Associated with Quantum Groups, Probability Measures on Groups X, (1991).
- SundaramRamchandran ,'Philosophical Ramblings on Some Mathematical Dichotomies and the Concept of Scale' , International Journal ofScientific Engineering and Technology , (www.ijset.com),) Volume No.1, Issue No.4, , pg : 28-34 ,Oct 2012.
- http://web.cecs.pdx.edu/~maier/cs584/Lectures/lect07b-11-MG.pdf
- XichunNie, VenkatKrovi, 'Fourier Methods for Kinematic Synthesis of Coupled Serial Chain Mechanisms', Transactions of the ASME ,232 , Vol. 127, MARCH 2005.
- Walter Rudin, 'Principles of Mathematical Analysis', Third Edition, 1976.
|