Research and Reviews - International Journals

International Journal of Innovative Research in Computer and Communication Engineering

Menu

ISSN ONLINE(2320-9801) PRINT (2320-9798)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Fractal Image Steganography Using Non Linear Model

G.Suryakala Eswari 1, N.Leelavathy2, U.Sandhya Rani 3
  1. Assistant Professor, Department of Computer Science & Engineering, Pragati Engineering College, Surampalem, A.P., India1
  2. Professor, Department of Computer Science & Engineering, Pragati Engineering College, Surampalem, A.P., India2
  3. Assistant Professor, Department of Computer Science & Engineering, Pragati Engineering College, Surampalem, A.P., India3
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

International Journal of Innovative Research in Computer and Communication Engineering

Abstract

The security of steganography system is improved by the scheme of steganography based on fractal images. Fractal image is a kind of non-linear graph. Fractal images can be easily generated using the non-linear model and computer graphics. But these images and their pattern depend upon initial conditions. In the proposed fractal image steganography, the secret information is inserted at the time of creation of fractal image by utilizing the initial parameters and the non-linear model. The fractal image that is generated at the sender side and receiver side are called as Cover-Image, and Stego-Image respectively. The receiver can extract secret information by comparing Stego-Image and Cover-Image with the same initial parameters. The effectiveness of steganography is amplified by combining it with cryptography and extending the non-linear model. So the security can be improved using RSA algorithm.

Keywords
Steganography, Fractal Image, Hausdorff, Escape Time Algorithm.

INTRODUCTION
Steganography is the art and science of hiding information by embedding messages within other digital multimedia objects, ostensibly harmless message. Steganography means “covered writing” in Greek. The steganography goal is to hide the presence of a message within another message called cover message [1-3]. So steganography can be seen as the complement of cryptography whose goal is to hide the content of a message. Steganalysis is the counterpart of steganography, as its goal is to detect the presence of hidden data.
The carriers commonly used include images, videos, audios, texts, two dimensional bar codes. Therefore, steganography in images, especially in natural images is popular. However, the natural images themselves exist as a kind of noise, which will significantly affect the embedding capacity of the steganography system. Generally, the carrier images can be downloaded conveniently from internet by anyone, including the attacker. The traditional natural image steganography often changed the inherent statistical characteristics which the original carrier images have, especially when the capacity of the information embedded is huge. Therefore, along with the development of the statistical model of all kinds of images, the security of the natural image steganography has met serious challenges [4-6]. Steganography in fractal images can be considered much more secure [7]. Although the fractal images, as a kind of non-linear graph, have very complex appearance, they can be easily generated on the basis of the combination of the nonlinear dynamic system model and the computer graphics.
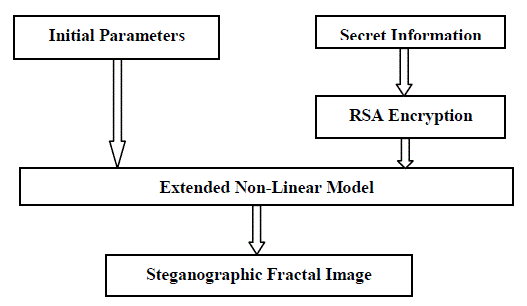
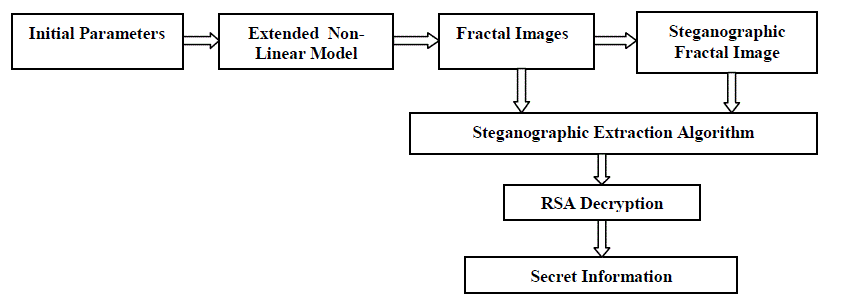
In this paper, a new method of fractal images steganography based on Julia set is proposed. The embedding of the secret information was simultaneous with the generation of the fractal images because the secret data themselves were regarded as the parameters necessary for the generation of fractal images. The structure of the steganography system in fractal images and a details of the algorithm will be described in Section II and III ,respectively. The experiment results will be shown and discussed in Section IV. Finally, practical and significant conclusions will be drawn in Section V.

II. RELATED WORK
Steganography in fractal images can be considered much more secure. Although the fractal images, as a kind of nonlinear graph, have very complex appearance. They can be easily generated on the basis of the combination of the nonlinear dynamic system model and the computer graphics.
The applications of fractal image theory has been proven in many fields, particularly in various applications of image steganography and compression. M. F. Barnsley has introduced the Iterated Function Systems (IFS) for the first time [8-12] based on the Self Similarity of fractal sets. Barnsley's proposed and assumed that many objects can be approximated by Self Similarity objects that are generated by the use of IFS transformations. Arnaud E. Jacquin has developed an algorithm to automated the method to find a set of transformations which resulted a good quality to the decoded images [13]. In Fractal coding methods based on Jacquin's work is to use the fact that different parts of the image at different scales are similar. In [14], an algorithm was proposed to embed the digital signature by modifying fractal features of the image whose robustness against JPEG compression was found to be high.
Fractal images can be generated by iterative calculation of a given non-linear model with the initial parameters followed with the specific computer graphic algorithms. The fractal images are generated through the given parameters, and requires a great amount of iterations to meet into the desire of an attractor, but at the same time, it provides non uniform randomness which does not independent upon the image size. One of the main advantages of this scheme is the amount of data to be hidden (embedded) is equal to that of the host signal while it is in general limited in the conventional data hiding schemes. Also both the opened fractal image and the hidden original one can be properly used depending on the situation. Unauthorized users will not notice the “secret” original image behind the fractal image, but even if they know that there is a hidden image it will be difficult for them to estimate the original image from the transformed image because random variables are used in the transformation process. Only authorized users who know the proper keys can regenerate the original image. The proposed method is applicable not only as a security tool for multimedia contents on web pages but also as a steganographic secret communication method through fractal images. The model of steganography system can be considered as a communication model with full side information when both the sender and receiver know the initial parameters, which can be transmitted as passwords in a reliable signal channel. While to the attacker, the model can be considered as a kind of model without side information or with incomplete side information. In other words, the carrier information in a fractal images steganography system is asymmetric to the receiver and the attacker. It is different from the natural images steganography system which has the same side information to the receiver and attacker.
The characteristics of fractal images are:
A. It has a fine structure at any arbitrarily small scale. It is too irregular to be easily described in traditional Euclidean geometric language.
B. It is self-similar or at least approximately similar. It has a simple and recursive definition.
C. Its Hausdorff dimension [15] is higher than its topological dimension.
The algorithm by Zhang [7] is that the fractal images were chosen as the carrier of information hiding. It has demonstrated the embedding and extraction technique. The proposed algorithm has shown increase in embedding capacity and security of the method with high Peak Signal to Noise Ratio (PSNR) as per the experimental results.

III. PROPOSED ALGORITHM BASED ON FRACTAL IMAGES
Escape Time Algorithm is one of the Non-linear Models. No exact fractal images of the same kind can be generated without initial parameters, even if the non-linear model is open. Therefore, to the sender and receiver, the model of steganographic system can be considered as a communication model with full side information when both the sender and receiver know the initial parameters. With the aid of computer graphics, fractal images with visual beauty can be created on the basis of fractal geometry. Plenty of fascinating images can be obtained when the parameters of the nonlinear dynamic system model changes during the generating of fractal images. Julia set is the maximal set of points that gets mapped onto itself under the function, and is usually created with the escape
time algorithm. For simplicity, in this study, we adopted quadratic polynomials of Julia set to create fractal images. The quadratic polynomials can be expressed as f z ? z ? c 2 ( ) ,where
A) Embedding Information: The embedding of the secret information was simultaneous with, while not after, the generation of the fractal images because the secret data themselves were regarded as the parameters necessary for generation of fractal images. Before embedding the secret data, encryption is done by using RSA algorithm. It increases the security of the steganographic system
Step 1: Assume fractal image size is a*b. Given c = p + qi, the escape radius threshold ??, and the escape time threshold ?? [where p , q, r , and t are Key Values]. Let l be the length of the secret message and the secret message is in the array s .
Initialise,
Complete Steps 2-4 for all points (nx,ny), where nx = 0,1,.,a-1, and ny = 0,1,…,b-1.
Step 2: Given starting values where min and min .
Set t = 0.
Step 3: Set
and t = t +1.
Step 4: Set r
If ?? > ?? and t ?T , read sequentially one bit from the secret information. If the bit is 0, the pixel ( , ) x y n n is drawn in predefined foreground colour. If the bit is 1, the pixel ( , ) x y n n is drawn in predefined background colour. Then go to step 2. If t=T, the pixel ( , ) x y n n is drawn in predefined background colour. Then go to step 2. If ?? > ?? and t ?T , go to step 3. As we can see from the above algorithm, the colour of each point of Julia set will be determined by the
secret information. Moreover, the existing probability of 0 or 1 in the secret information is generally about 50%, respectively, because the secret information usually has been encrypted beforehand. The information is encrypted by using RSA algorithm. Therefore, as a result, the colour of about half Julia Set points will change from foreground colour to background colour. This is why the generated fractal image is blurred and the steganographic fractal image looks different with the image without secret information. In order to solve this problem, we partition the escape time threshold T.
For example, the points of Julia set are considered as important points and not be embedded when t ?1/ 2T and ?? > ?? . Embedding only occurred when t ?1/ 2T and ?? > ??. Finally we get two images at sender (stego image) and receiver side (cover image).
B) Extracting Information: The extracting algorithm is almost the same as the embedding algorithm. Complete the Step 1 to 3 of the embedding algorithm, then calculate 2 2 t t r ? x ? y . If ?? > ?? and t ?T , get the colour of point ( , ) x y n n and compare with steganographic fractal image. If the colour is the same, then the secret information is 0, while if the colour is not the same, the secret information is 1. If t ?T, the colour of point ( , ) x y n n is ignored. Therefore, the essence of this algorithm is extracting the colour information of each point of Julia Set and compared with steganographic fractal image to extract the secret information. The information is decrypted by using RSA .

IV. RESULTS
In this study, secret data is embedded with the algorithm described previously. The initial parameters at sender and receiver side of p and q were set as -0.194 and -0.861, respectively. The escape radius threshold R was set as 1000, and the escape time threshold T was set as 100. To add more security RSA prime numbers were taken as 37 and 41 and encryption key set as 13. Figure 3 and Figure 4 shows the images generated at sender and receiver side respectively. The experimental results shown in Table I reveals that, for a given embedding capacity [32 ×32] the PSNR is high for proposed algorithm in addition to Root Mean Square Error (RMSE) value to be low making the perceptual quality of the image as that of original image.

V. CONCLUSION
In this project, the fractal images were chosen as the carrier of information hiding due to the ease of generation and amend characteristics of fractal images and the algorithm is implemented with MATLAB 2012a. Compared with traditional image-based information hiding methods, the sources of the fractal image carriers are richer to hold more information without notice, and this method can offer better resistance against various stego-analysis. The beauty and complexity of this fractal image steganography system was increased by extending non-linear model and introducing cryptographic technique to the system.
The multiple generation of the fractal images is poor because of the randomness of generation. Therefore, in the future, the developers should focus on how to generate acceptable fractal image without affecting embedding capacity by using new non-linear model, changing colour scheme, etc.
 

Tables at a glance
Table icon
Table 1
 

Figures at a glance
Figure 1 Figure 2 Figure 3 Figure 4
Figure 1 Figure 2 Figure 3 Figure 4
 

References